改进郊狼算法用于直线阵列零陷综合
国 强,李佳莹,王亚妮
(哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150000)
直线阵列的阵列综合因其在雷达、通信、卫星、遥感等各类无线系统中的应用而备受关注[1-2]。通常通过控制天线阵列的相位、激励幅值和阵元位置形成期望的特定形状的阵列天线方向图,如约束主瓣宽度(First Null Beam Width,FNBW)、指定方向上的零陷深度(Null Depth Level,NDL)、最优旁瓣电平(SideLobe Level,SLL)等。在当今干扰普遍存在的电磁环境中,某些方向上的电磁干扰会严重影响接收到的有用信号,由于主瓣方向指向目标接收机,旁瓣和零陷指向干扰方向,因此,具有零陷深度的阵列综合有着重要的研究意义[3-4]。
随着智能优化算法的不断发展,选择恰当的优化算法仍是目前阵列综合的一个极具实际意义的研究课题。遗传算法(Genetic Algorithm,GA)[5]被应用到具有最小旁瓣电平和零陷控制的直线阵列综合中,然而遗传算法的局部搜索能力较差,运算费时,在进化后期搜索效率较低。KHODIER[6]将布谷鸟算法(Cuckoo Search,CS)用于直线天线阵列综合中,通过优化阵元的相位来抑制旁瓣电平并获得所需的零陷,然而算法的不稳定性导致收敛结果容易受参数大小和初始种群的影响。文献[7]将基于生物地理学的优化算法(Biogeography-Based Optimization,BBO)应用于线阵零陷综合,在抑制旁瓣电平的同时得到零陷,然而容易出现早熟收敛的现象。文献[8]利用Taguchi 优化算法(Taguchi's Optimisation)进行均匀激励的直线阵列综合,通过优化阵元相位得到最优旁瓣电平和零陷深度,但收敛速度和收敛精度仍然不能满足需求。并且无免费午餐定理[9]指出,没有一种算法可以完美地解决每一个优化问题,它们都有各自的优点和局限性。
郊狼优化算法(Coyote Optimization Algorithm,COA)[10]由PIEREZAN等于2018年提出,在解决优化问题的过程中展现出较强的优化能力。与上述算法相比,郊狼优化算法具有不同的算法结构、可调参数更少、更易实现等特点,为平衡探索和开发提供了新的机制,有着更好的收敛性能和优化精度。然而,在解决复杂的阵列天线综合问题时,郊狼优化算法仍存在收敛速度慢、易陷入局部最优等问题。针对上述问题,笔者提出了改进郊狼算法(Improved Coyote Optimization Algorithm,ICOA),在郊狼算法的基础上,引入了次优个体变异策略并提出了全局最优组内引导策略,提高局部搜索能力、加快收敛速度。利用ICOA通过仅控制天线阵元的相位合成期望的阵列方向图。
1 直线天线阵列模型
直线天线阵列(Linear Antenna Array,LAA)是由偶数(2N)个具有各向同性的阵元沿x轴对称放置组成的。为了不失一般性,阵因子Af(φ)如下表示[11-12]:
(1)
(2)
其中,N为x正半轴上的阵元个数,In为第n个阵元的激励幅值,k=2π/λ为波数,λ为阵列工作波长,xn为第n个阵元的位置,φ为转向角,αn为第n个阵元的激励相位,di为阵元间距。
优化目标是只控制直线阵列的相位αn(激励幅值和阵元位置等同于均匀直线阵列,In=1,di=λ/2)形成单点、多点的零陷值和最低的旁瓣电平,把直线阵列的相位作为优化变量,寻找最优相位以形成期望的阵列方向图。阵因子Af(φ)简化为
(3)
为了提升算法的搜索速率,采用权重控制的方式构建适应度函数。适应度函数F由以下两部分组成:
(4)
其中,C1和C2为适应度函数的权重,式(4)等号右边第1项为旁瓣电平最小化的适应度函数,第2项为零陷深度的适应度函数。k为指定零点的个数,φk为第k个零点的角度。
2 改进郊狼优化算法
郊狼算法是通过模拟自然界中郊狼种群的群居生活来解决优化问题的,包括初始化种群并随机分组、组内郊狼成长、生死、被组驱逐和接纳等过程。其中每组的郊狼个体都代表着一个优化问题的解,由郊狼的社会状态映射得到阵元的实际相位,由适应度函数式(4)作为衡量该解是否为直线阵列零陷综合中最优相位的标准。
2.1 次优个体变异策略
为了保持种群多样性,避免算法陷入局部最优,变异无疑是最好的举措。然而,如果令全部郊狼个体发生变异,将损失大量优质解且花费时间在非优质解的求取中,于是提出次优个体变异策略。将郊狼个体按适应能力升序排列,在次优个体(序列后30%的郊狼)中引入Hybrid映射[13]扰动,在小范围内发生变异,提高种群多样性,扩大搜索空间,增加抗局部最优能力。次优个体变异的更新方式为
sncw=scw+κ(2p2-1) ,
(5)
(6)
其中,scw和sncw分别为变异前后次优个体的社会状态;κ为变异系数,取κ=0.1;p为Hybrid映射扰动项,由式(6)得出;且μ1=1.8,μ2=2.0,b=0.85。
2.2 全局最优组内引导策略
传统郊狼算法中,组内郊狼的成长受最优α狼影响δ1和组内文化趋势uj影响δ2。然而,由于初始随机分组,无法保证每组α狼和组文化倾向uj的质量,很容易出现组内最优个体引导能力不足、陷入局部最优及收敛速度慢的情况。并且,次优个体变异策略在提高种群多样性的同时,会增加算法整体的计算量和降低收敛速度。为解决这个问题,在传统郊狼算法每个郊狼的成长受δ1和δ2影响的基础上,构建一种新型的成长方式,提出全局最优狼αG的组内引导δ3。通过全局最优的引导,使算法更快地接近全局最优解,跳出局部最优并加快收敛速度。郊狼的成长方式更新为
(7)
(8)
nc=sc+(g/gM)(r1δ1+r2δ2)+(1-g/gM)(r3δ3) ,
(9)
其中,uj为组内文化趋势(O为按升序排序的郊狼的社会状态分布),通过计算组内所有郊狼的中位数获得;Nc为组内郊狼个数。cr1、cr2、cr3为组内随机选取的郊狼,αG为全局最优狼,sc、nc为初始和更新后的郊狼社会状态,g为当前迭代次数,gM为最大迭代次数,r1、r2和r3分别表示δ1、δ2和δ3的随机权重,且为[0,1]区间均匀分布的随机数。
算法求解过程中,优化前期,当前迭代次数g远小于最大迭代次数gM,g/gM是一个较小的数,新的社会状态主要由(1-g/gM)(r3δ3)全局最优狼引导;到了优化后期,反之,g/gM数值较大,新的社会状态主要由(g/gM)(r1δ1+r2δ2)组内最优狼和文化倾向引导。组内的郊狼成长后,由式(4)对其进行适应能力评估,保留优质个体参与其他郊狼的成长,加快算法的收敛速度。
考虑到郊狼的出生和死亡属于自然事件,郊狼算法计算狼的年龄用year表示,新生郊狼由种群中随机两个父母郊狼结合而产生并受环境因素影响。
Ps=1/D,Pa=(1-Ps)/2 ,
(10)
其中,Ps和Pa分别为分散概率和关联概率,决定了新生郊狼的遗传和变异情况,D为优化问题的维度。根据对新生郊狼的社会适应能力进行评估来决定新生郊狼的生死。
种群中郊狼会以Pe的概率被组驱逐和接纳,驱逐概率取决于组内成员的个数Nc,驱逐机制可以帮助种群的文化交流即物种多样化。
(11)
2.3 ICOA算法伪代码
① 设置参数:郊狼组数Np,组内郊狼个数Nc,最大迭代次数gM,随机初始化郊狼种群并随机分组
② 由式(4)评估每个郊狼的社会适应能力,确定全局最优郊狼α
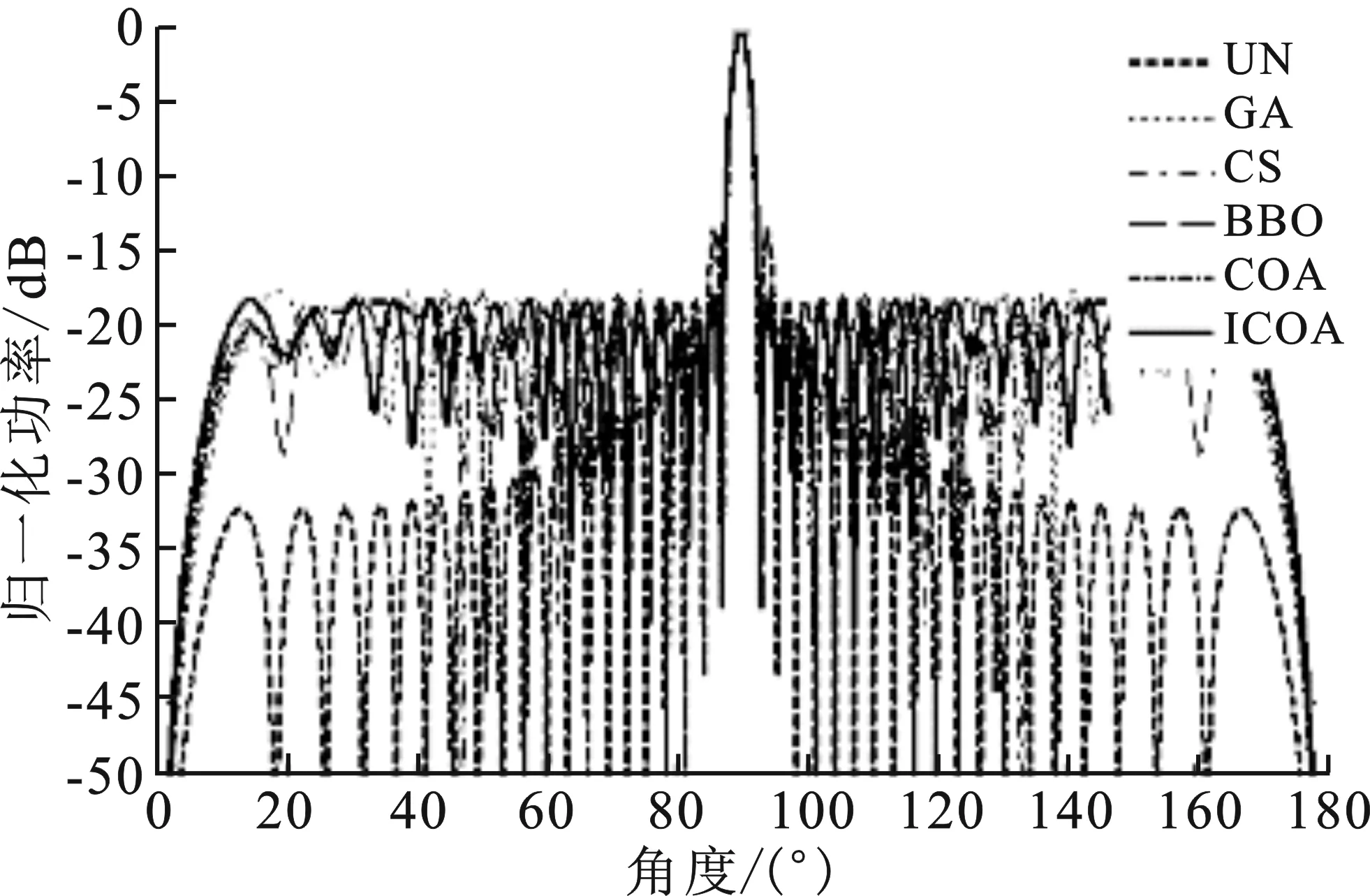
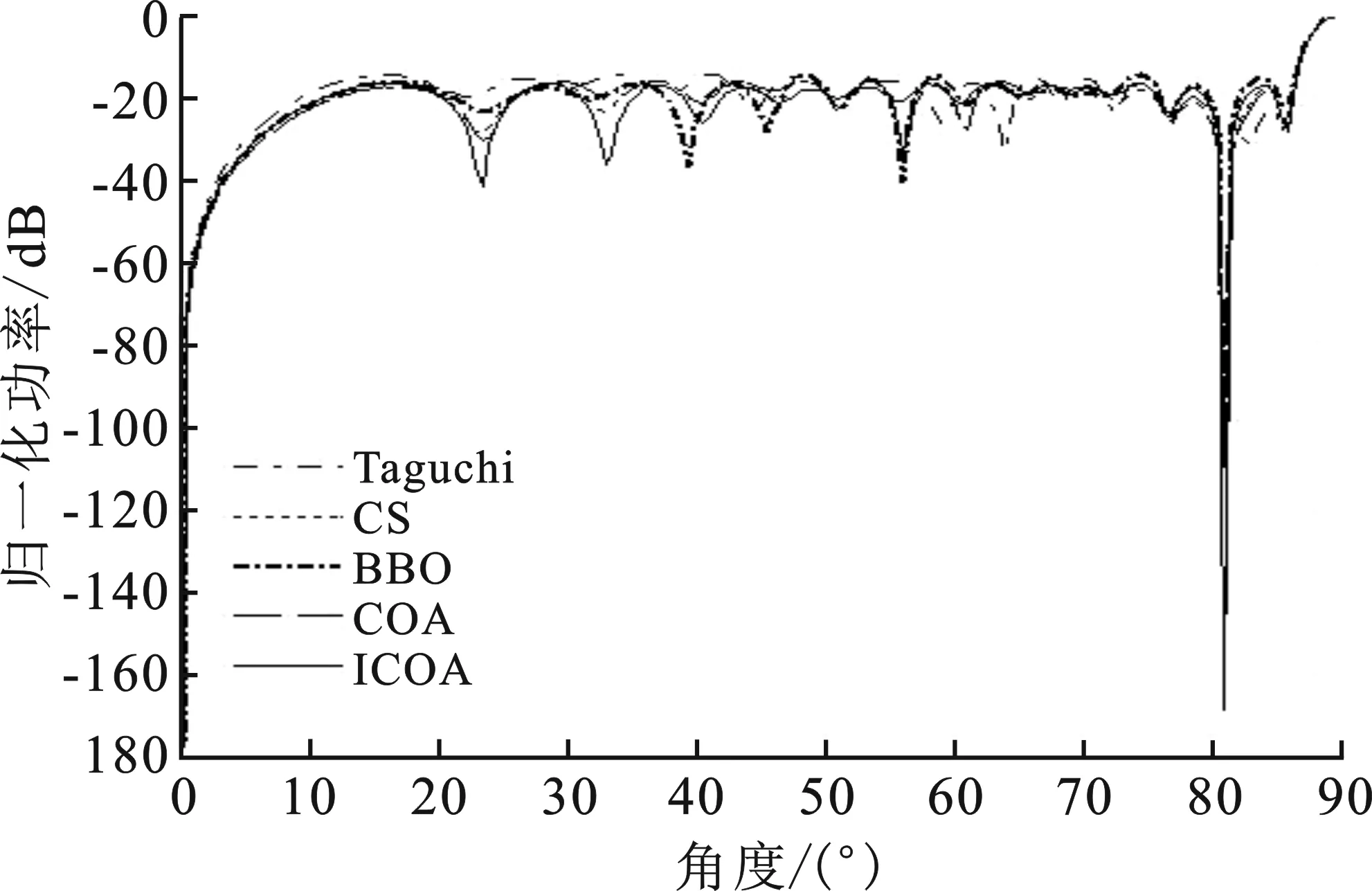
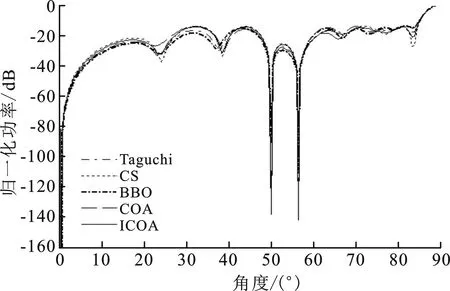
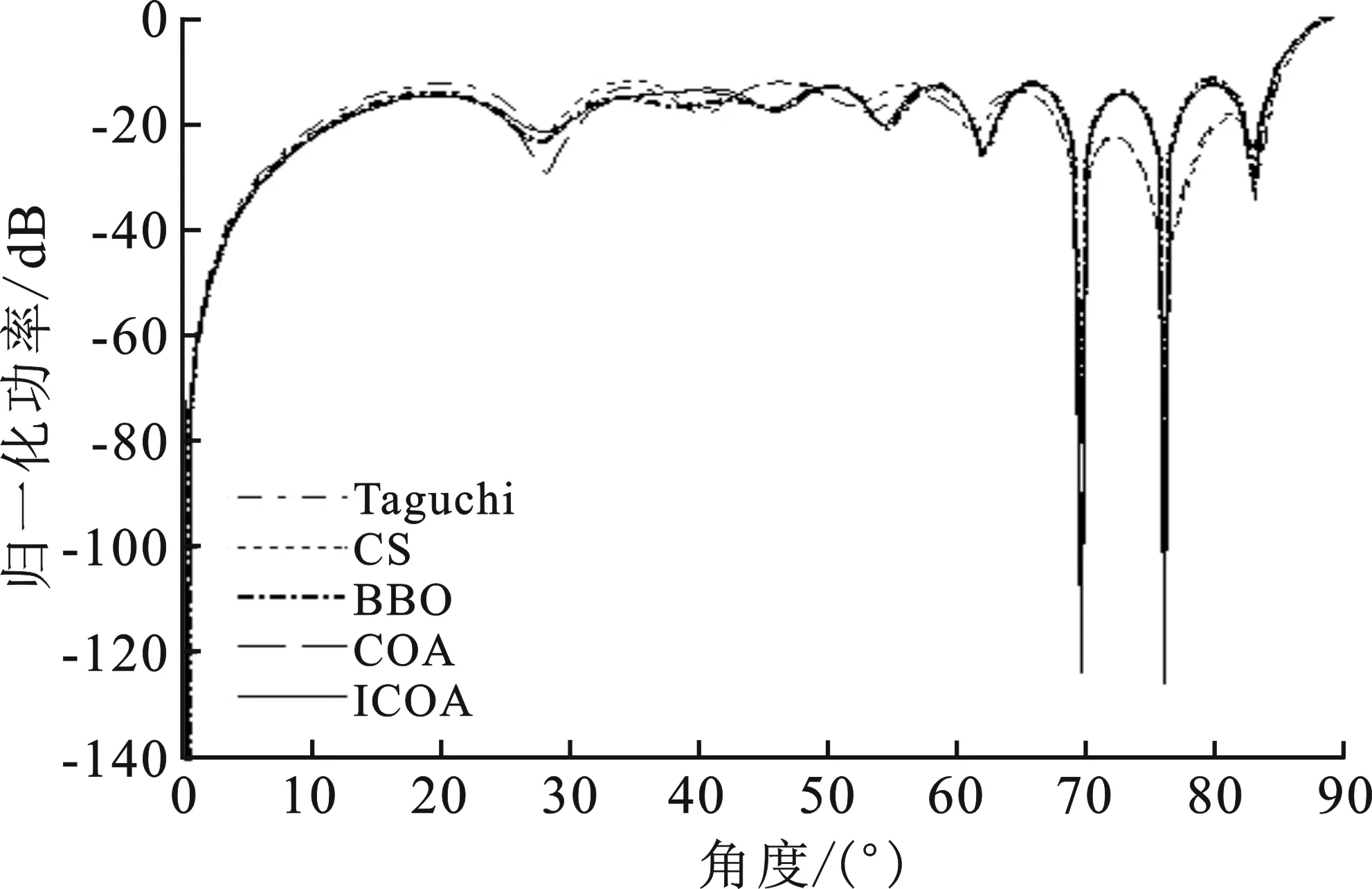
③ whileg ④ forp=1 to Npdo ⑤ 得到组内最优的α狼,利用次优个体变异策略提高种群多样性,如式(5)和(6) ⑥ 根据式(7)计算组文化趋势u ⑦ forc=1 to Ncdo ⑧ 根据式(8)计算郊狼成长受到的影响δ1、δ2和δ3 ⑨ 利用全局最优组内引导策略,由α、u和αG引导郊狼成长,如式(9) ⑩ 保留全局最优郊狼αG 为验证所提改进郊狼算法在旁瓣抑制和指定方向上的零陷深度优化中的有效性和优越性,笔者针对不同的阵元个数和相位进行仿真实验,以阵元相位为优化变量,寻找最优相位以形成期望的阵列方向图,并将实验结果与遗传算法、郊狼算法、布谷鸟算法[6]、基于生物地理学的优化算法[7]和Taguchi算法[8]相比较。所有实验中,阵元间距和激励幅值等同于均匀直线阵列,ICOA参数设置如下:Np=10,Nc=10,最大迭代次数gM为10 000D。实验的硬件环境为Inter Core i5、1.6 GHz、8 GB,软件环境为Windows 10、MATLAB R2014a。 为了证明改进郊狼算法的有效性,首先从郊狼算法改进前后的寻优性能和收敛能力着手分析。 次优个体变异策略中引入的Hybrid映射是Tent映射和Logistic映射的结合。为与单一的Logistic映射和Tent映射比较,分别在次优个体变异策略中引入Hybrid映射、Tent映射和Logistic映射,对12、24、36、48和60阵元进行阵列综合,从而达到抑制旁瓣电平的目的。图1给出了统计结果。从图中可以得出,在旁瓣电平抑制方面,引入Hybrid映射的改进郊狼算法优于单一的Tent映射、Logistic映射和原郊狼算法,且原郊狼算法寻优能力弱于引入次优个体变异策略的改进郊狼算法。 图1 不同阵元数目的旁瓣峰值电平对比图 采用改进郊狼算法对30阵元直线阵列进行优化,优化目的为抑制最大旁瓣电平。图2表现了分别执行原郊狼算法、仅执行了改进郊狼算法的次优个体变异策略和执行了改进郊狼算法的次优个体变异策略和全局最优组内引导策略的最大旁瓣电平,可以得出,执行改进郊狼算法的次优个体变异策略和全局最优组内引导策略获得的旁瓣电平优于仅执行改进郊狼算法的次优个体变异策略,且仅执行改进郊狼算法的次优个体变异策略的旁瓣电平优于原郊狼算法;在算法收敛速度方面,原郊狼算法的在第22代收敛,执行改进郊狼算法的次优个体变异策略在第45代收敛,执行改进郊狼算法的次优个体变异策略和全局最优组内引导策略在第10代收敛,收敛速度最快。综上所述,改进郊狼算法引入Hybrid映射效果最好,且在寻优能力和收敛速度上都强于原郊狼算法。 图2 不同算法旁瓣峰值电平对比图 3.2.1 最大旁瓣电平抑制 分别使用改进郊狼算法、遗传算法、郊狼算法,布谷鸟算法[6]和基于生物地理学的优化算法[7]对40阵元仅控制相位进行阵列优化,所有实验都在同等条件下进行,D=20,其他参数设置如上。由仿真结果可以得出,改进郊狼算法在主瓣零点带宽为6.4°的情况下得到了-18.27 dB的旁瓣电平,与均匀直线阵(UNiform linear array,UN)相比,改善了6.03 dB,优于遗传算法的-17.39 dB、郊狼算法的-18.15 dB、布谷鸟算法的-17.59 dB、基于生物地理学的优化算法的-17.96 dB,算法的运行时间为661.05 s。图3描述了40阵元优化相位的阵列方向图,图4描述了上述算法优化40阵元线阵的收敛性与迭代次数的关系。可以得出,改进郊狼算法的寻优能力和收敛速度都明显优于上述对比算法。 图3 40阵元优化相位的阵列方向图 图4 40阵元收敛性与迭代次数的关系对比图 为证明改进郊狼算法的稳定性,设计40次蒙特卡罗试验对40阵元仅控制相位进行阵列优化。图5为40次蒙特卡罗实验结果。表1为统计分析结果,其中,改进郊狼算法的最优旁瓣电平和平均旁瓣电平最小,最大旁瓣电平抑制效果最好,且方差最小,相比于对比算法,有着良好的稳定性。因此,在最大旁瓣电平抑制方面,相比遗传算法、郊狼算法,布谷鸟算法和基于生物地理学的优化算法,改进郊狼算法在寻优能力、收敛速度和稳定性方面具有明显的优势。 图5 40次蒙特卡罗实验对比图 表1 40次蒙特卡罗实验统计分析结果 3.2.2 直线阵列零陷综合 将改进郊狼算法、郊狼算法、布谷鸟算法[6]、基于生物地理学的优化算法[7]和Taguchi算法[8]应用于直线阵列零陷综合中,优化目标为抑制最大旁瓣电平并获得最低的指定方向上零陷深度。实验1是32阵元在单一零点方向(81°)上的零陷深度优化和旁瓣电平抑制,适应度函数权重设置如下:C1=1,C2=2,D=16,其他参数设置同上。实验2、3分别是20阵元在50°、56.5°方向和69.5°、76°方向上的零陷深度优化和旁瓣电平抑制,适应度函数权重设置为C1=1,C2=2,D=10,其他参数设置同上。 由仿真结果可以得出,实验1改进郊狼算法得到的最优旁瓣电平为-16.71 dB,相比郊狼算法、布谷鸟算法、基于生物地理学的优化算法和Taguchi算法分别改善了0.27 dB、1.03 dB、2.02 dB和2.03 dB,81°方向上零陷深度为-168.4 dB,明显优于对比算法,仿真运行时间为547.98 s。实验2、3中,就抑制旁瓣电平方面,改进郊狼算法得到的最优旁瓣电平分别为-16.71 dB和-12.93 dB,实验2相比郊狼算法、布谷鸟算法、基于生物地理学的优化算法和Taguchi算法分别改善了0.29 dB、1.03 dB、2.02 dB和0.06 dB,实验3相比上述算法分别改善了0.31 dB、0.72 dB、1.16 dB和0.66 dB;就加深零陷方面,实验2在50°和56.5°方向上零陷深度为-153.9 dB 和-142 dB,实验3在69.5°和76°方向上零陷深度为-125.1 dB和-123.6 dB,两个实验获得的零陷深度均明显优于对比算法,实验2、3的仿真运行时间分别为289.23 s和292.00 s。 图6至图8分别为相应的最优阵列方向图。图9为改进郊狼算法在3个实验中的收敛曲线图,表2为3个实验的仿真结果。可以得到,3个对比实验中,改进郊狼算法得到的旁瓣电平和零陷深度都明显优于对比算法。因此,在旁瓣电平抑制和零陷深度联合优化中,相比郊狼算法、布谷鸟算法、基于生物地理学的优化算法和Taguchi算法,改进郊狼算法在寻优能力和收敛速度方面依然具有明显的优势。 图6 32阵元在81°方向上的阵列方向图 图7 20阵元在50°、56.5°方向上的阵列方向图 图8 20阵元在69.5°、76°方向上的阵列方向图 图9 ICOA在三个实验中的收敛曲线图 表2 ICOA、COA、CS、BBO和Taguchi仿真结果对比 针对智能优化算法在具有最小旁瓣电平和零陷深度的均匀激励非周期直线阵列零陷综合中存在收敛速度慢及易于陷入局部最优的问题,提出了一种基于改进郊狼算法的直线阵列综合。在郊狼算法的基础上,提出次优个体变异策略和全局最优组内引导策略,以提高种群多样性,增强寻优能力,并加快算法的收敛速度。仿真结果表明,与遗传算法、郊狼算法、布谷鸟算法、基于生物地理学的优化算法和Taguchi算法相比,改进郊狼算法在最大旁瓣电平抑制和零陷深度优化中都具有更快的收敛速度和更好的寻优精度与稳定性。同时,笔者所提方法为其他阵型的阵列综合提供了新的思路,后续该算法将被应用在其他复杂的非线性优化问题中,如零陷加宽、余割平方方向图优化等。3 实验结果及分析
3.1 改进郊狼算法性能分析


3.2 阵列天线方向图综合





4 总 结

