几种发射波束零陷展宽算法仿真分析
吴若增
(中国电子科技集团公司第三十八研究所,安徽 合肥 230088)
0 引言
在作战场景复杂的现代战场中,电子对抗愈演愈烈,这极大压缩了雷达等有源装备生存空间。为应对敌方反辐射导弹、干扰机、侦察机等威胁,以及各种雷达对抗场景,发射波束置零技术得到广泛应用,以此提高我方雷达生存率。发射波束置零技术是指我方雷达在敌方干扰机、侦查机等设备所在方向上不发射功率,或者发射功率极低,即发射波束图在所在方向上形成零陷,使敌方设备无法对我方雷达进行侦查截获。
但由于机械平台抖动、干扰侦察设备运动、系统测角误差等因素,雷达发射波束图零点位置容易出现偏移。因此,采用发射波束零陷展宽技术手段,即在置零方向上形成宽零陷,使得雷达系统对置零方向估计或置零方向先验信息存在一定误差的条件下,仍可在置零方向区间形成零陷。
目前常用的发射波束零陷展宽算法有Capon零陷展宽算法、导数约束零陷展宽算法、正交投影零陷展宽算法、线性约束零陷展宽算法、Mailloux零陷展宽算法、静态波束零陷展宽算法和导向矢量重构零陷展宽算法等。本文对以上算法在特定场景进行仿真分析,比较以上算法性能,给出仿真结论,为在算法工程化应用方面提供一定的指导意义。
1 算法介绍
1.1 Capon零陷展宽算法
Capon零陷展宽算法是对零陷区间的导向矢量进行积分,然后进行空域滤波,即可在置零方向上形成零陷展宽。

式中:w为权向量,Q为零陷区间构成的数据矩阵;α(θ0)为置零方向的导向矢量。
对w求梯度,令其为零,可得Capon零陷展宽算法的最优权向量表示为:

1.2 导数约束零陷展宽算法
导数约束零陷展宽算法是让方向图函数和其高阶导数在零点方向上为零[1,2],即可在置零方向上形成零陷展宽。
令波束图函数f(θ)对φi=2πdsinθi/λ的高阶导数在θi,i=1,…,K处为零,其中λ为雷达工作波长,d为阵元间距,θi为置零方向,共K个置零方向。即:

式中:B=diag(0 1…M-1);M为阵元数。由上式可得BmwHa(θ)θ=θi=0,即权矢量w投影到由向量Bma(θi)构成的(1+q)K维正交补空间中。因此,可以得出w满足如下关系式:

AJ为置零方向的导向矢量矩阵。因此w可以表示为:

1.3 正交投影零陷展宽算法
正交投影零陷展宽算法引入施密特正交化(GSO)的思路[3,4],采用递推的方式来进行正交补空间的推导,不需要矩阵求逆运算,可得到最佳权的表达式为:

式中:P为置零方向正交投影补空间。
1.4 线性约束零陷展宽算法
线性约束零陷展宽算法是零陷展宽算法直接推广[5,6],在Capon零陷展宽算法中,约束条件只有wHa(θ0)=1。而线性约束零陷展宽算法包含多个约束条件,具体表示为:

其中,C∈CM×(L+P)代表约束矩阵,f∈C(L+P)×1代表对应的约束响应向量。这时的条件极值问题可以描述为

对式求梯度,可得线性约束零陷展宽算法的权向量为

1.5 Mailloux零陷展宽算法
Mailloux零陷展宽算法[7,8]主要思想是构造一个锥化矩阵T对导向矢量矩阵Rr进行拓展,即令

式中:“°”表示Hadamard乘法。对于锥化矩阵T的构造,Mailloux方法为

式中:L表示为虚拟置零点的数量;δ为虚拟置零点在sinθ域的间隔。假设零陷在sinθ的宽度为W,则δ=W/(L-1)。
假设期望方向的导向矢量为,可得Mailloux的零陷展宽算法权向量为

1.6 静态波束零陷展宽算法
静态波束零陷展宽算法原理是从静态波束控制的角度,对权值进行二次约束,达到零陷展宽的目的[9]。
约束方程为:

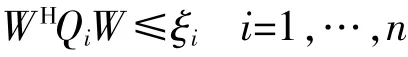
利用Lagrange乘子可得静态波束零陷展宽算法权向量为:

2 仿真分析
通过Matlab仿真实验,对本文介绍的算法进行仿真实验,主要分析单零点、不同零陷宽度条件下仿真实验的结果。
仿真条件:20阵元的均匀线阵,阵元间距为半个波长。假设期望方向为0°,置零方向为-40°。
2.1 Capon零陷展宽算法
图1给出了Capon零陷展宽算法在不同零陷宽度时的波束图。如图1所示,在不同的零陷宽度时,零陷的深度也有所不同。当零陷宽度较小时,零陷深度越深;零陷宽度较大时,零陷深度较浅。总体来说,用Capon零陷展宽算法在单置零角度时,零陷深度满足在-100dB以下。
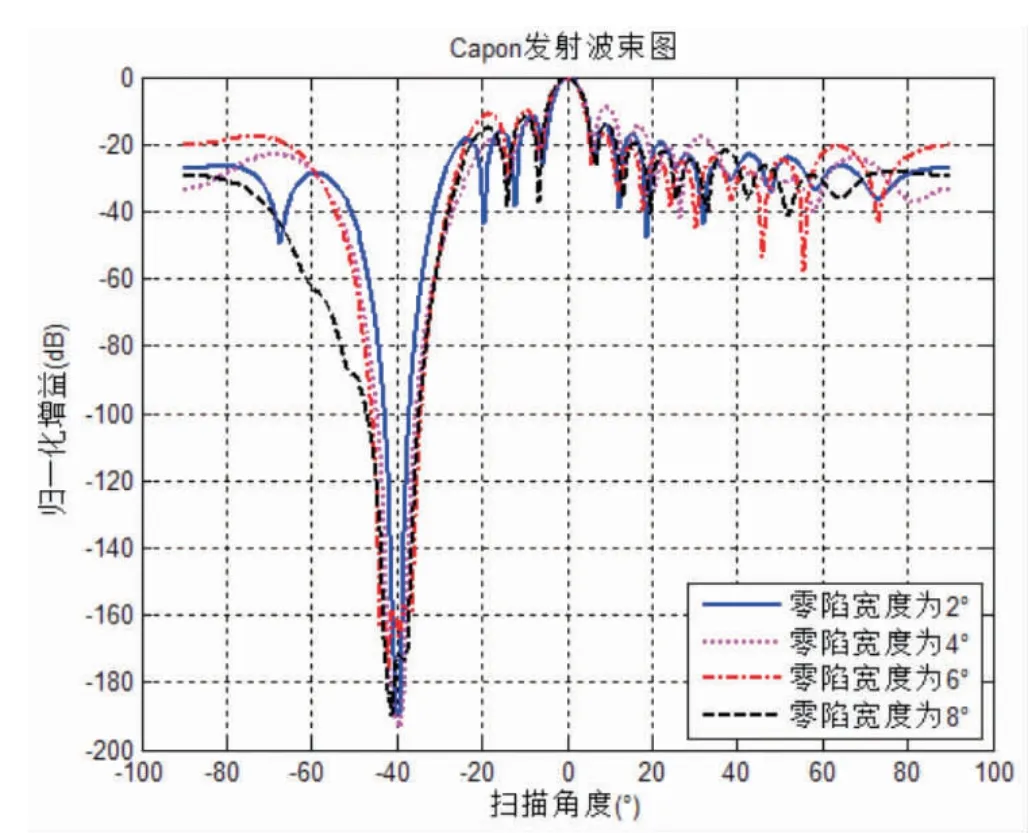
图1 不同零陷宽度时的Capon零陷展宽算法波束图
2.2 导数约束零陷展宽算法
导数约束零陷展宽算法零陷宽度与求导阶数相关,求导阶数越大,零陷宽度也越宽。图2是导数约束零陷展宽算法在不同的求导阶数时的波束图。
从图2中可以看出,零陷宽度、零陷深度与求导阶数相关。在求导阶数较小时(小于6阶),随着求导阶数的增大,其零陷宽度和零陷深度也会随之变宽变深,可以达到-200dB以下;当求导阶数较大时(大于8阶),零陷宽度会显著变宽,但零陷深度也随之变浅,增益提升到-130dB以下。
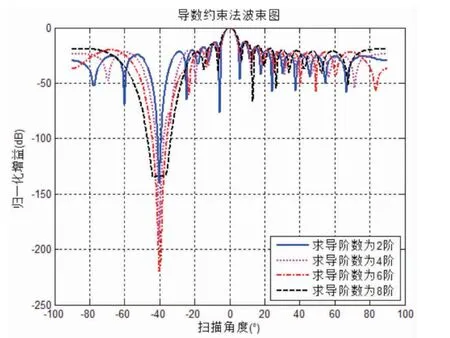
图2 不同求导阶数时的导数约束零陷展宽算法波束图
2.3 正交投影零陷展宽算法
图3给出了正交投影零陷展宽算法在不同零陷宽度时的波束图。
由图3可知,随着零陷宽度的增大,零陷深度也逐渐抬高,当零陷宽度为8°时,零陷深度抬高到了-80dB。零陷宽度的变化没有影响波束图的主瓣和旁瓣,即在其他方向上不受零陷宽度的影响,具有一定的稳定性。
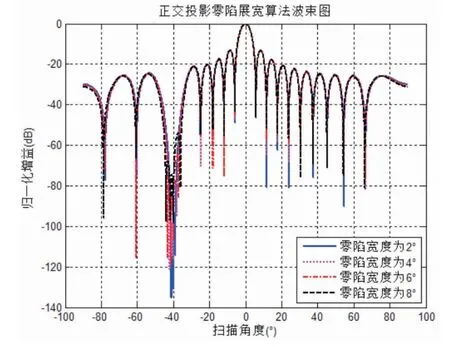
图3 不同零陷宽度时的正交投影零陷展宽算法波束图
2.4 线性约束零陷展宽算法
图4给出了线性约束零陷展宽算法在不同零陷宽度时的波束图。
由图4可知,线性约束零陷展宽算法随着零陷宽度的增加,零陷深度加深,同时波束图的旁瓣抬高。当零陷宽度进一步增大时,可使波束图失效。
2.5 Mailloux零陷展宽算法
图5给出了Mailloux零陷展宽算法在不同零陷宽度时的波束图。
由图5可知,Mailloux零陷展宽算法具有较稳定的零陷深度,维持在-80dB左右,除零陷区间外,波束主瓣和旁瓣受零陷影响较小,同正交投影零陷展宽算法类似,具有一定的波束稳定性。
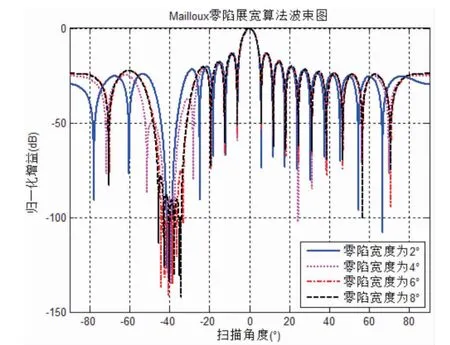
图5 不同零陷宽度时的Mailloux零陷展宽算法波束图
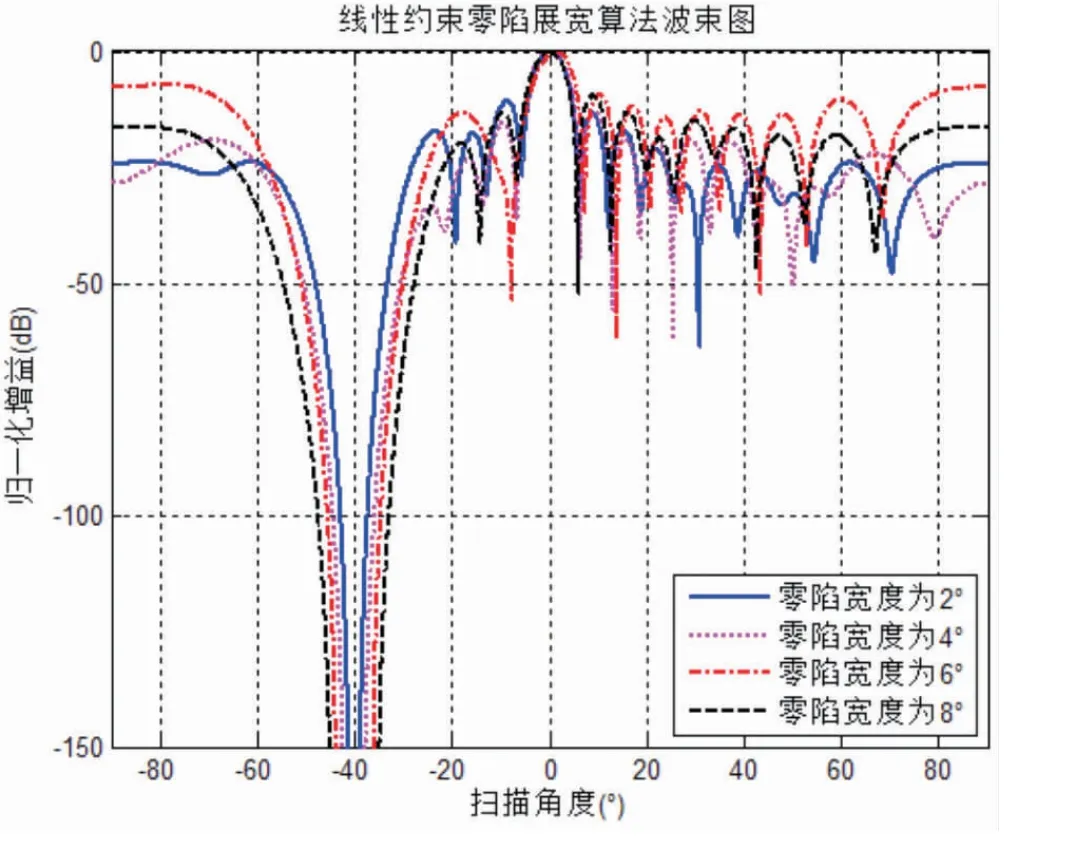
图4不同零陷宽度时的线性约束零陷展宽算法波束图
2.6 静态波束零陷展宽算法
图6 给出了静态波束零陷展宽算法在不同零陷宽度时的波束图。
由图6可知,静态波束零陷展宽算法在不同的零陷宽度条件下,零陷深度一直维持在-65dB左右,同时旁瓣幅度没有出现抬升现象,具有一定的波束稳定性。
2.7 导向矢量重构零陷展宽算法
图7给出了导向矢量重构零陷展宽算法在不同零陷宽度时的波束图。
由图7可知,导向矢量重构零陷展宽算法所产生的零陷宽度比理论要求的宽度较窄,零陷深度也比其他零陷展宽算法较浅。随着零陷宽度的增大,零陷深度逐渐抬升,但对波束图的主瓣和旁瓣无影响,故导向矢量重构零陷展宽算法也具有一定的波束稳定性。

图7 不同零陷宽度时的导向矢量重构零陷展宽算法波束图
3 结语
本文介绍了几种发射波束零陷展宽算法,并对单零点、不同零陷宽度条件下进行仿真分析。其中Capon零陷展宽算法、导数约束零陷展宽算法、线性约束零陷展宽算法在宽零陷时保持了较深的零陷宽度,可以达到以下;正交投影零陷展宽算法不包含矩阵求逆运算,具有快速、灵活的特点;Mailloux零陷展宽算法、静态波束零陷展宽算法、导向矢量重构零陷展宽算法对波束主瓣和旁瓣影响较小,但静态波束零陷展宽算法零陷深度一直维持在左右,导向矢量重构零陷展宽算法零陷宽度比理论要求的宽度较窄。
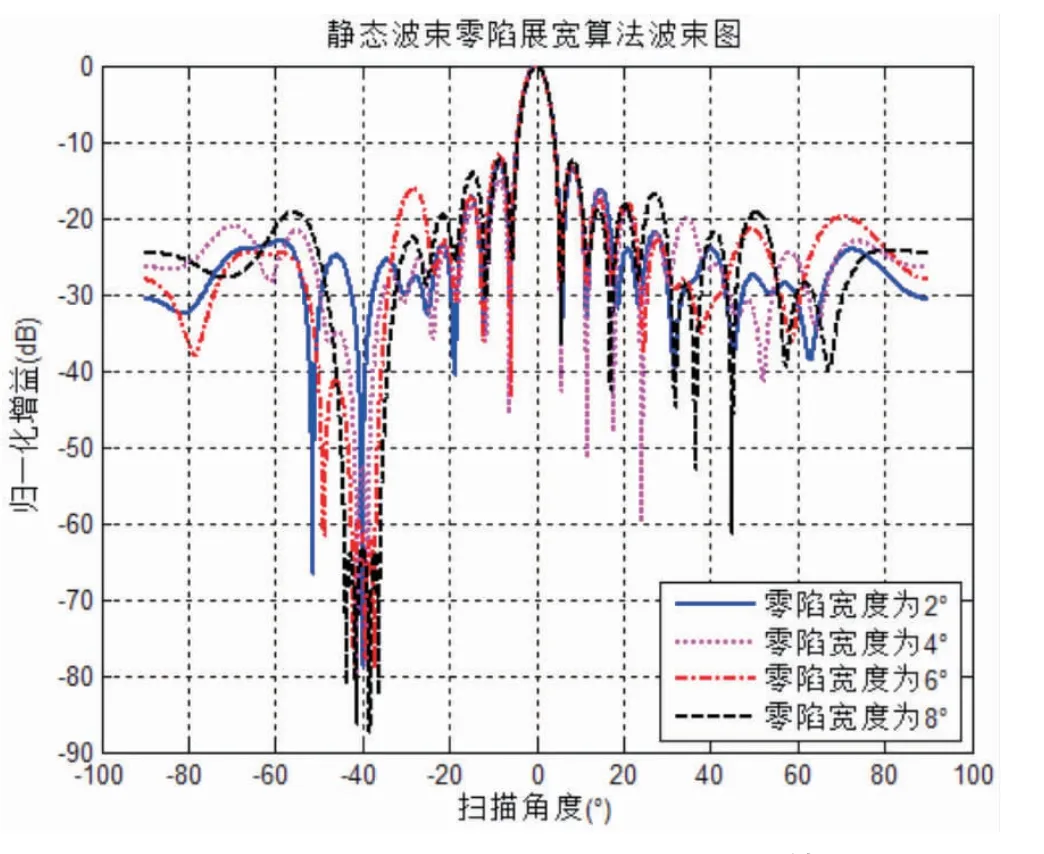
图6不同零陷宽度时的静态波束零陷展宽算法波束图

