不同线路条件对车辆动力学性能的影响

摘要：  为探查不同曲线半径和线路激励对车辆动力学性能的影响，应用动力学方法建立车辆-轨道系统动力学模型，计算各动力学评价指标的变化情况。研究结果表明：增加曲线半径有利于增加车辆通过曲线的安全性;车辆经过曲线线路连接处时脱轨概率较大，可重点考虑曲线线路连接位置车辆的运行状态;适当增大曲线半径可以减少轮轨间磨耗，有效降低车轮与轨道的磨耗速度;轨道激励变化对车辆临界速度的影响较大，可根据实际运行工况计算最佳临界速度范围。

关键词：  车辆-轨道系统; 曲线; 参数; 轨道激励; 动力学性能

中图分类号：  U213.213; TB115.1文献标志码：  B

Influence of different line conditions

on vehicle dynamic performance

QI Xin

（Department of State-Owned Assets， Jiangsu Normal University， Xuzhou 221116， Jiangsu， China）

Abstract： To explore the influence of different curve radius and line excitation on the vehicle dynamic performance， the dynamic model of vehicle-track system is established using dynamic method， and then the change of each dynamic evaluation index is calculated. The results show that increasing the curve radius is conducive to increasing the safety of vehicles passing through the curve. The derailment probability is high when the vehicle passes through the curve line connection， so the  running state of the vehicle at the connection position of the curve line can be mainly considered. The wear between wheel and rail can be reduced by properly increasing the curve radius， and the wear speeds of the wheels and tracks can be reduced effectively. The change of track excitation has great influence on the critical speed of vehicles， and the optimum critical speed range can be calculated according to the actual operating conditions.

Key words： vehicle-track system; curve; parameters; track excitation; dynamic performance

收稿日期：  2021-08-17修回日期：  2021-09-08

基金项目：  江苏师范大学博士学位教师科研启动项目（19XSRX015）

作者简介： 齐心（1987—），女，辽宁锦州人，硕士，研究方向为车辆系统动力学，（E-mail）355444716@qq.com0引言车辆与轨道是相互作用的系统，车辆运行安全性与线路各参数联系紧密，即车辆必须在一定的线路条件下满足动力学性能要求[1]。高速铁路的线路设计需要满足行车安全平顺，保证旅客乘坐舒适，并兼顾线路维修方便[2]。轮轨间相互作用的加剧对线路设计提出更高要求，轨道线路由直线、缓和曲线和圆曲线组成，在不同线路条件下，轮轨接触状态时刻发生变化。在良好的线路设计下，车辆各动力学性能指标均在安全范围内，因此车辆横向和垂向动力学性能相对较好。选择合理的曲线参数不仅可以避免由于脱轨系数过大导致列车脱轨，而且可以提高曲线通过能力、改善轮轨间作用力、降低轮轨磨耗。针对车辆动力学性能与线路参数之间的关系，国内外学者在轮轨间相互作用方面进行大量研究。KUFVER[3]研究缓和曲线长度、圆曲线长度、夹直线长度以及轨道不平顺对旅客乘坐舒适性、车辆运行平稳性、行车稳定性和车辆安全性的影响。KRZYZTOF[4]对车辆在曲线道路上运行的动力学问题进行深入研究，认为轨道不平顺对车辆动力学性能和临界速度存在一定的影响。MIYAGAKI等[5]分析日本常用的几类缓和曲线线型对车辆动力响应的影响，并提出一种新型缓和曲线线型。王开云等[6]利用车辆-轨道耦合动力学理论，开发具有自主知识产权的车辆-轨道系统仿真软件TTISIM，并利用该软件建立具有实际意义的车辆-軌道评价体系。王开云等[7]基于系统工程思想，运用车辆-轨道耦合动力学理论研究小半径曲线线路。魏庆朝等[8]根据车辆-轨道纵向动力学基本理论，采用车辆纵向运动仿真系统研究线路的纵断面参数与列车安全运行的关系。常卫华[9]运用有限元分析软件Ansys建立车辆-轨道系统模型，研究横向力对线路和道岔等的影响，结果认为轨道受到大于250 kN横向力时车辆易发生倾覆。丁勇等[10]研究车辆曲线通过性能的影响因素，认为适当增加圆曲线半径或延长缓和曲线长度可以提高曲线通过能力，但在小半径曲线线路上增加缓和曲线长度对车辆曲线通过能力的影响较小。ZHAI等[11]和高建敏等[12]研究轨道不平顺对车辆动力学性能的影响规律，得到车辆运行速度在250～400 km/h范围内时长波域不平顺敏感波长的范围。本文主要从轨道线路参数和车辆动力学性能指标之间的关系入手，综合讨论车辆运行安全性、行车平稳性和曲线通过能力受线路参数的影响规律。采用动力学软件建立车辆-轨道系统模型，基于直线与曲线工况下车辆的动力学响应差异，研究不同曲线半径和线路激励对车辆动力学性能的影响。

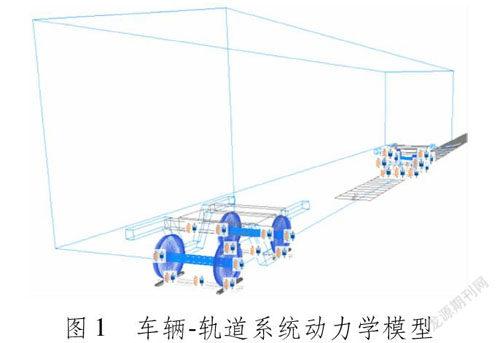
1动力学模型创建轮对、转向架、车体及其各部件间的连接力元，建立车辆-轨道系统模型（见图1）。为更加符合实际运行工况，轨道激励采用实测轨道谱，车轮踏面为LMA型踏面。

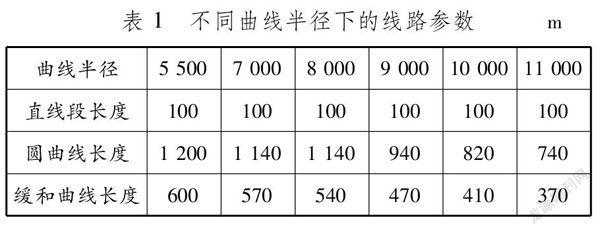
在保证车辆安全通过曲线的前提下，设置车辆速度为300 km/h，该速度既可以满足高速要求，又符合实际运行条件。选取曲线半径分别为5 500、7 000、8 000、9 000、10 000和11 000 m。车辆高速通过曲线时会受到离心力的作用，车轮轮缘与外侧钢轨接触，影响行车安全，因此曲线轨道均设有超高。本文曲线超高均设置为110 mm（过超高），计算模型中的其他线路参数见表1。

2线路参数对车辆动力学性能的影响由于轮轨间复杂的相互作用，车辆运行时在横向和垂向产生振动，严重时可能影响旅客乘车的舒适度和货物的完整性。在保证安全的首要前提下，通过车辆系统动力学评价指标，即稳定性、平稳性和曲线通过能力，对车辆及其子结构的运行进行全方位评价。

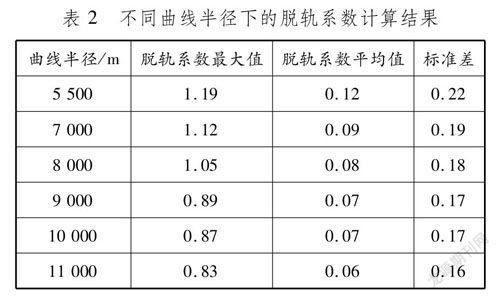
2.1运行安全性分析安全性是车辆运行的基本要求。安全性分析主要考虑防止脱轨的稳定性、防止蛇行运动的稳定性以及防止车辆倾覆的稳定性，对应指标分别为脱轨系数、轮重减载率和倾覆系数。不同曲线半径下的脱轨系数计算结果见表2。车辆过半径为5 500～11 000 m的曲线线路时，脱轨系数均满足评定标准的第一限度范围，其值大多分布在1.20以下，少数产生较大幅度的波动，原因是可能受到来自线路的激励作用。曲线半径5 500 m对应的脱轨系数均值与曲线半径7 000 m对应的脱轨系数均值相差0.03，大于其他相邻曲线半径之间0.01的差值，说明在此阶段增加曲线半径可以改善和提高行车安全。随着曲线半径增大，脱轨系数均值逐渐减小，车辆稳定性不断提高。由脱轨系数的标准差可以看出，随着曲线半径增大，脱轨系数波动变小，说明曲线半径越大，车辆运行安全性与稳定性越好。

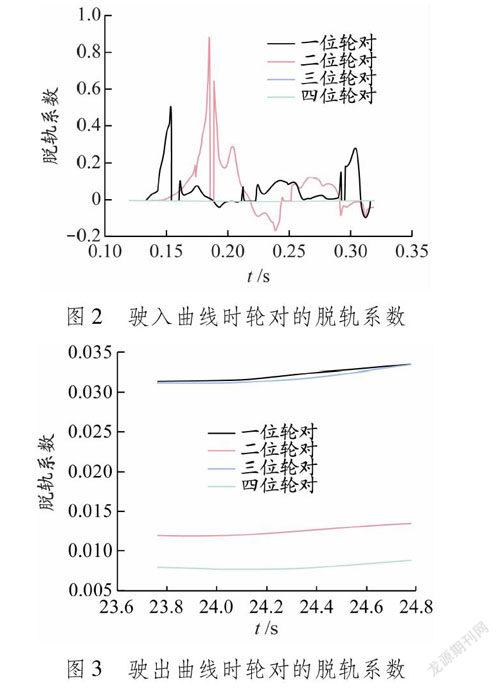
以曲线半径为9 000 m的良好工况为例，研究车辆所有轮对的脱轨系数变化规律。选择2个特殊的时间段进行分析，一段是从直线转为缓和曲线，另一段是从缓和曲线转为直线，即驶入曲线与驶出曲线2个阶段。根据线路参数和车辆运行速度可知，车辆约在0.12 s时进入曲线，在23.70 s时驶出曲线，出、入曲线时轮对的脱轨系数变化见图2和3。

车辆驶入曲线时，由于一位轮对（前轮）具有导向功能，比其他轮对更快地受到线路激励作用，其脱轨系数发生剧烈波动，大于其他轮对驶入曲线时的值，随后一位轮对脱轨系数逐渐下降并趋于平稳。三位轮对相对于其他轮对变化平缓，轮轨接触状态最好，因此后续以三位轮对作为参照进行动力学性能分析。车辆驶出曲线时，4个轮对的脱轨系数变化都不大，基本保持在均值附近，说明车辆驶出曲线时没有受到剧烈的轮轨间作用力，运行稳定。综合来看，当车辆经过曲线线路连接处时易产生较大波动，车辆发生脱轨的概率变大，建议重点观察曲线线路连接位置的车辆通过速度以及车辆运行状态，保证车辆安全有效运行。

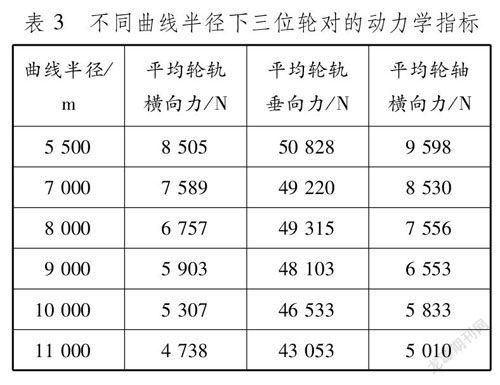
2.2轮轨间的作用力车辆曲线通过指标主要包括防止车辆脱轨的稳定性、防止车辆倾覆的稳定性以及轮轨磨耗性能[13]，指标好坏直接影响车辆运行安全，这里主要评价轮轨间作用力和轮轨磨耗性能。在保持车辆曲线通过安全的前提下，对轮轨间作用力加以限制。轮轨间作用力主要有轮轨横向力、轮轨垂向力和轮轴横向力，曲线线路参数与表2相同，分析在不同曲线半径条件下三位轮对的受力情况，结果见表3。

在不同曲线半径下，仿真模型运行得到的动力学性能响应结果均在规定的允许范围之内，即车辆以300 km/h的速度均能安全通过各曲线，但各曲线通过性能指标有所不同。随着曲线半径的增大，轮轨横向力逐渐减小，在曲线半径为5 500 m时其数值最大。该曲线轮轨横向力峰值出现在缓和曲线上，此时过大的轮轨横向力使得轮轨作用加劇，对车辆通过曲线产生消极影响。在各曲线半径下，轮轨垂向力相差较小（1 kN以内），其数值均小于我国铁路建设规定的垂向力峰值Pmax=170 kN，车辆通过曲线时虽出现轮重偏载，但依然保持良好的垂向动力学性能。随着曲线半径的增大，轮轴横向力逐渐减小，且其变化趋势与轮轨横向力的变化趋势相似，只是数值略有不同。综合以上分析可知：在不改变线路其他参数的情况下，曲线半径越大，车辆通过曲线的动力学性能越好;车辆在缓和曲线运行时，小半径曲线轮轨横向力较大，因此应尽量降低该路段的轮轨横向力。

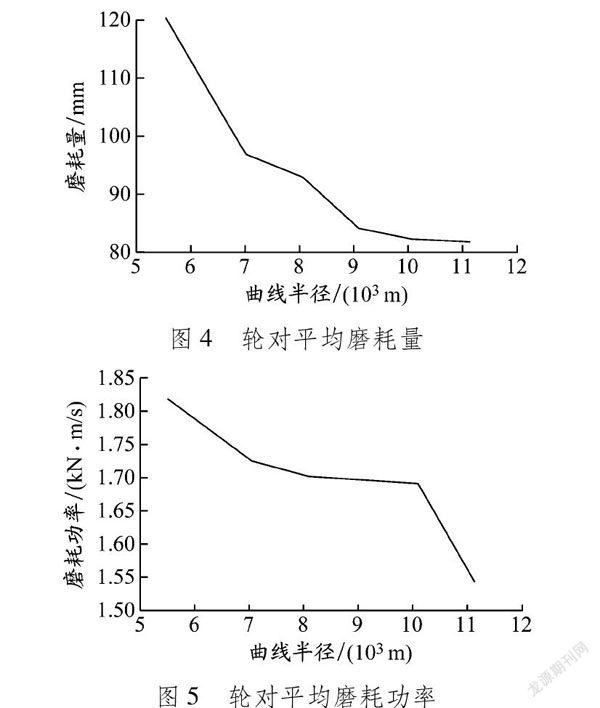
2.3轮轨磨耗车辆通过曲线时，轨底坡作用导致轮对发生偏载，钢轨与车轮间产生较大作用力，不同曲线半径下轮对的磨耗量和磨耗功率变化情况见图4和5。

磨耗量的变化曲线大致可以分为5段。第一段为曲线半径5 500～7 000 m，此阶段磨耗量急剧下降，对应的磨耗功率也下降，说明曲线半径相对较小时轮轨间作用尤为剧烈，轮轨间磨耗较大。第二段为曲线半径7 000～8 000 m，第三段为曲线半径8 000～9 000 m，第二段的磨耗量变化比第三段缓慢，磨耗功率在这2段中均下降。第四段为曲线半径9 000～10 000 m，此阶段磨耗量和磨耗功率曲线趋于水平状态，说明曲线半径的变化对轮轨磨耗影响较小。第五阶段为曲线半径10 000～11 000 m，磨耗量的变化与第四段基本相同，接近于水平，但磨耗功率出现大幅度下降。由此可以看出，适当增加曲线半径可以减小轮轨间作用，有效降低磨耗速度，但是第四段的轮轨磨耗相对平稳，改变曲线半径对轮轨磨耗影响较小。

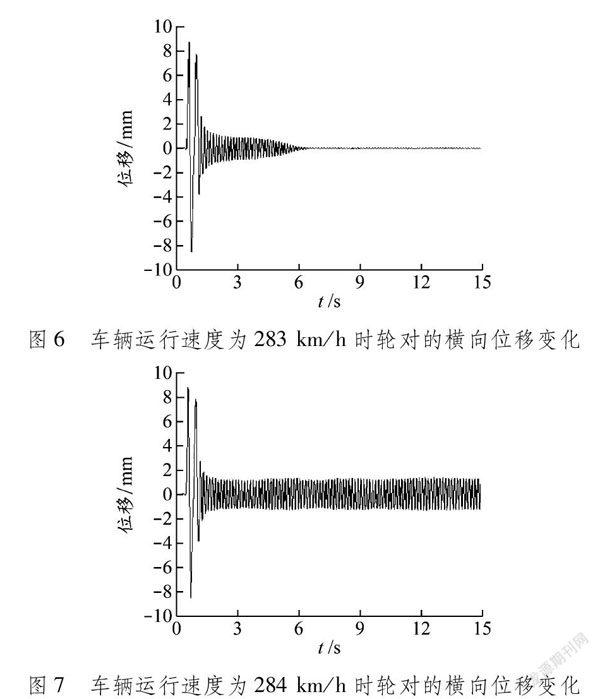
2.4临界速度临界速度是评价车辆稳定性的重要指标。选取2种不同类型的轨道激励，分析在车辆不同运行速度下轮对的横向位移变化情况。以A型激励为例，车辆运行速度为283 km/h时轮对的横向位移变化见图6。轮对的横向位移经过6 s的横向波动后衰减至平衡位置并最后收敛。车辆运行速度为284 km/h时轮对的横向位移变化见图7，此时横向位移无法收敛。由此可以说明，在A型激励下，车辆运行的非线性临界速度应为284 km/h，车辆的实际运行速度应尽量保持在此数值附近，以保证车辆安全平稳运行，避免脱轨。

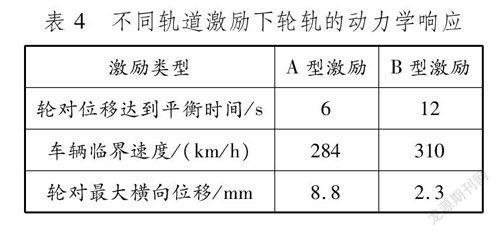
不同轨道激励下轮轨的动力学响应见表4。在B型轨道激励下，车辆临界速度为310 km/h，比A型激励下大9.15%;B型激励轮对位移量达到平衡的时间为12 s，为A型激励平衡时间的2倍。此外，与A型激励下相比，B型激励下的轮对最大横移量较小，其数值仅为A型激励的26%。

在不同轨道激励作用下，车辆的非线性临界速度变化较大，应根据实际行车条件进行模拟，使仿真尽量贴近实际运行工况，得到最佳临界速度范围，以避免脱轨事故发生。

3结论运用动力学软件建立车辆-轨道系统模型，研究不同曲线半径和线路激励对车辆动力学性能的影响，得出以下结论。（1）随着曲线半径增大，脱轨系数均值逐渐减小，数值波动趋于平稳，车辆稳定性不断提高。车辆在缓和曲线运行时，小半径曲线轮轨横向力较大，应尽量考虑如何降低该路段的轮轨横向力。（2）车辆经过曲线线路连接处时轮轨作用力易产生较大波动，车辆发生脱轨的概率变大，建议重点观察曲线线路连接位置处的车辆通过速度以及车辆运行状态，保证车辆安全有效运行。（3）适当增加曲线半径可以减少轮轨间磨耗，有效降低磨耗速度;曲线半径为9 00 m～10 000 m时轮对的磨耗量和磨耗功率趋于平衡状态，说明此阶段曲线半径的变化对轮轨磨耗影响较小。（4）在不同轨道激励作用下，车辆的非线性临界速度变化较大，应根据实际运行工况进行模拟，得出最佳临界速度范围，避免发生脱轨事故。参考文献：

[1]李晓芹. 重载铁路线路圆曲线几何参数对通过性能的影响及参数分析[D]. 北京： 北京交通大学， 2014.

[2]佟立本. 高速铁路概论[M]. 5版. 北京： 中国铁道出版社， 2017： 34-40.

[3]KUFVER B. Optimization of horizontal alignments for railways： Procedures involving evaluation of dynamic vehicle response[EB/OL].（2001-01-02）[2021-08-16]. https：//trid.trb.org/view/686991.

[4]KRZYZTOF Z. Dynamical investigation of railway vehicles on curved track[J]. European Journal of Mechanics： A/Solids， 1998， 17（6）： 1001-2020. DOI： 10.1016/S0997-7538（98）90506-X.

[5]MIYAGAKI K， ADACHI M， SATO Y. Analytical study on effects of form in transition curve[J]. Vehicle System Dynamic， 2004， 41（S1）：657-666.

[6]王云开， 瞿婉明. 车辆-轨道耦合动力学仿真软件TTISIM及其试验验证[J]. 中国铁路科学， 2004， 25（6）： 49-54. DOI： 10.3321/j.issn：1001-4632.2004.06.009.

[7]王云开， 瞿婉明， 刘建新， 等. 山区铁路小半径曲线强化轨道动力性能[J]. 交通运输学报， 2005， 5（4）： 15-19. DOI： 10.3321/j.issn：1671-1637.2005.04.004.

[8]魏慶朝， 张庆珩. 列车纵向力与线路纵断面参数[J]. 北方交通大学学报， 1995， 19（2）： 153-158.

[9]常卫华. 重载铁路横向力对钢轨倾覆影响研究[J]. 铁道工程学报， 2011（2）： 71-73. DOI： 10.3969/j.issn.1006-2106.2011.02.014.

[10]丁勇， 曲金娟， 田光荣， 等. 重载铁路货车结构强度考核标准中纵向力取值的研究[J]. 中国铁道科学， 2015， 36（5）： 94-103.DOI： 10.3969/j.issn.1001-4632.2015.05.14.

[11]ZHAI W M， GAO J M， LIU P F， et al. Reducing rail side wear on heavy-haul railway curves based on wheel-rail dynamic interaction[J]. Vehicle System Dynamics， 2014， 52（S1）： 440-454. DOI： 10.1080/00423114.2014.906633.

[12]高建敏， 翟婉明， 王云开， 等. 高速行车条件下轨道几何不平顺敏感波长研究[J]. 铁道学报， 2012， 34（7）： 83-88. DOI： 10.3969/j.issn.1001-8360.2012.07.013.

[13]陈鹏， 高亮. 线路参数对高速车辆曲线通过性能的影响[J]. 工程建设与设计， 2007（6）： 66-67. DOI： 10.3969/j.issn.1007-9467.2007.06.020.（编辑武晓英）