跨中作用下铝合金卷边工字形截面受弯构件的稳定性能

姜超 林冰

摘要：  为研究跨中作用下铝合金卷边工字形截面构件的弹塑性稳定性能，采用有限元方法分析腹板高厚比、翼缘宽厚比、卷边宽厚比、载荷作用点位置等参数对构件稳定性的影响。结果发现：构件屈曲模式与构件长度有关;腹板高厚比越大，稳定系数曲线越低，说明增大腹板高度可有效提高承载力，但相对承载能力下降;翼缘宽厚比越小，稳定性能越好;增加卷边宽度可提高卷边自身的抗弯刚度，增强对翼缘的约束作用，从而提高稳定性;降低横向载荷作用点位置有利于构件保持稳定和提高承载力。有限元计算结果可验证相关规范中的公式对此类受弯构件的适用性。

关键词：  铝合金; 受弯构件; 弯扭失稳; 稳定系数; 有限元

中图分类号：  TU395; TB115.1文献标志码：  B

收稿日期：  2021-08-30修回日期：  2020-09-28

作者简介： 姜超（1996—），男，山东平原人，硕士研究生，研究方向为铝合金稳定性，（E-mail）1907889914@qq.com;

林冰（1968—），男，回族，辽宁凌源人，教授级高工，博士，研究方向为钢结构设计理论与施工，（E-mail）linbing@cscectc.comFlexural stability of aluminum alloy curling I-section member

under mid-span action

JIANG Chao1， LIN Bing1，2

（1. College of Civil Engineering， Shandong Jianzhu University， Jinan 250101， China;

2. Technical Center， China State Construction Engineering Co.， Ltd.， Beijing 101300， China）

Abstract： To study the elastic-plastic stability of aluminum alloy curling I-section members under midspan action， the effects of web height-thickness ratio， flange width-thickness ratio， curling width-thickness ratio and the load position on the stability of members are analyzed by finite element method. The results show that the buckling mode is related to the length of the member; the larger the web height-thickness ratio is， the lower the stability coefficient curve is， and it shows that increasing the web height can effectively improve the bearing capacity， but the relative bearing capacity decreases; the smaller the flange width-thickness ratio is， the better the stability is; the flexural stiffness of the curling can be improved by increasing the curling width， and the constraint effect on the flanges is enhanced， and then the stability can be improved; lowering the position of lateral load is beneficial to maintaining stability and improving bearing capacity. The applicability of the formula in the relevant code to this kind of flexural members can be verified by finite element calculation results.

Key words： aluminum alloy; member; flexural; torsional-flexural buckling; stability coefficient; finite element

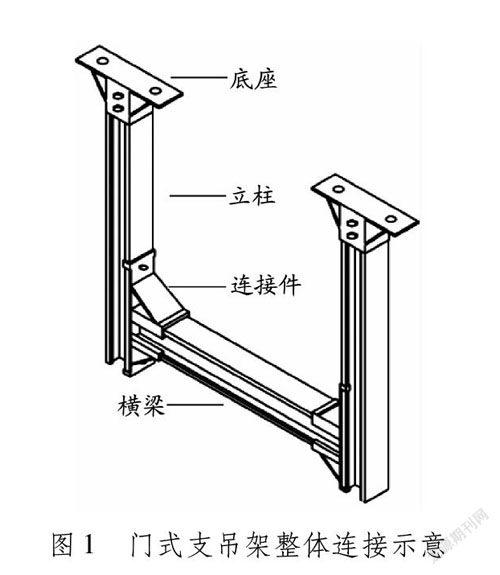
0引言鋁合金材料具有质量轻、强度高、美观、耐腐蚀、低温韧性好、可挤压成型、可循环利用等优点，在现代建筑领域中被广泛应用。《铝合金结构设计规范》（GB 50429—2007）[1]的制定和推广，大大推动铝合金材料在建筑领域中的应用。近年来，铝合金材料被逐渐应用到装配式支吊架[2-4]中，典型铝合金门式支吊架整体连接示意见图1。

铝合金门式支吊架由底座、立柱、连接件和横梁等组成，立柱和横梁均为铝合金卷边工字形截面构件。国内外对铝合金轴压构件的研究比较深入和广泛，而有关铝合金受弯构件的试验研究和有限元分析工作较少，尤其是在国内，这方面的研究才刚起步。吴亚舸等[5]开展H形截面构件的跨中加载试验，采用数值分析与试验相结合的手段拟合Perry-Robertson形式的铝合金梁弯扭屈曲承载力计算公式;郭小农等[6]针对H形和T形截面铝合金构件，分别进行跨中单点加载和四分点两点加载试验研究;石永久等[7]针对H形截面构件进行纯弯试验，认为钢结构规范中关于受弯构件整体稳定性的设计方法不能直接应用到铝合金构件的设计中，并给出建议公式;翟希梅等[8]针对铝合金箱形截面构件进行三点弯曲试验，基于直接强度法，提出考虑材料非线性特征和构件初始缺陷的受弯承载力计算方法。本文针对6061-T6铝合金门式支吊架横梁的卷边工字形受弯构件，运用有限元分析软件Abaqus，分析在跨中集中载荷作用下其腹板高厚比、翼缘宽厚比、卷边宽厚比、载荷作用点位置等参数对横梁整体稳定性的影响，并与无卷边工字形梁进行对比分析。将有限元分析结果与我国规范、欧洲规范及石永久等[7]建议公式中的稳定系数计算方法进行对比，验证规范公式对此类截面受弯构件的适用性。

1有限元试件及模型

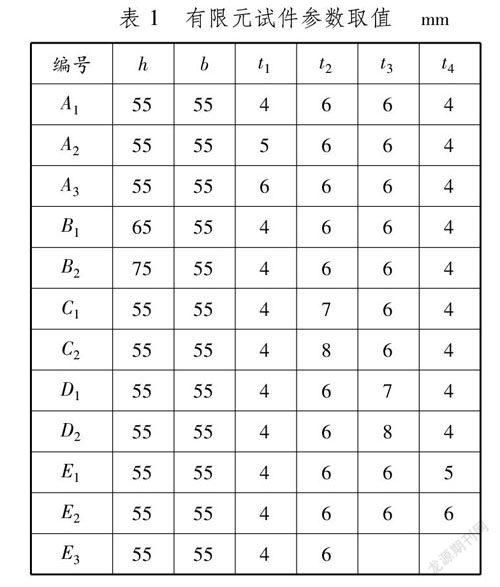
1.1有限元试件设计支吊架用铝合金构件卷边工字形截面见图2。腹板厚度t1、翼缘厚度t2、卷边厚度t3、卷边宽度t4和截面高度h为变量，截面宽度b=55 mm为定值，标准对照组截面高度h=55 mm。根据国家建筑标准设计图集《装配式管道支吊架（含抗震支吊架）》（18R417-2）[9]和《铝合金支吊架系统技术规程（报批稿）》推荐的常用截面尺寸，选取腹板厚度t1、截面高度h、翼缘厚度t2、卷边厚度t3和卷边宽度t4等5个影响因素，每个影响因素取3个数值，采用正交分析法设计5个系列有限元试件，见表1。

受弯构件的整体稳定影响因素有截面尺寸、初弯曲、初偏心和残余应力等。铝合金构件的制作一般采用挤压成型技术，加工过程中会出现板件厚度不均匀的情况，在拉伸校直过程中会出现Bauschinger效应[10]。在有限元软件模型中，初始几何缺陷、材料的Bauschinger效应和板件厚度不均匀等影响统一设定，构件初始变形为梁长的1/1 000[10]，构件初始变形的形式选择特征值屈曲分析中的1阶模态。铝合金构件的弹性模量较小，大约为钢材弹性模量的1/3，因此铝合金构件中的残余应力不如钢材中的显著，铝合金挤压型材中的残余应力更小，其影响可以忽略不计[10-11]。

1.26061-T6铝合金的本构关系目前，广泛使用的铝合金本构模型是Ramberg-Osgood模型，即ε=σE00.002σf0.2n式中：σ为材料应力;ε为材料应变;E0为材料的弹性模量;f0.2为名义屈服强度，取0.2%残余应变所对应的应力值;n为描述材料应变硬化的参数，取n=f0.2/10。利用SANS试验机进行单向静力拉伸试验[12]，6061-T6铝合金的力学性能参数见表2。其中：fu为极限抗拉强度;At为断裂伸长率;υ为泊松比的平均值。

1.3有限元模型采用Abaqus软件进行有限元分析，铝合金卷边构件模型采用4节点减缩积分壳单元S4R，能够形象反映结构特征及其受力特点，达到预期效果。边界条件为两端夹支[13]，在跨中施加集中载荷，载荷作用点设在上翼缘，并在截面剪心处及下翼缘设置对照组，加载方式为位移控制加载，卷边工字形构件夹支示意见图3，其有限元模型见图4。考虑到端部效应以及便于支撑，构件两端分别伸出支座100 mm。

有限元计算主要包括2个步骤：第一步，对铝合金构件进行特征值屈曲分析，得到弹性阶段内构件的1阶屈曲模态（见图5），选择1阶屈曲模态作为构件的初始变形形状，并将1阶屈曲模态坐标值乘以一定比例系数作为初始缺陷值加载到模型中;第二步，采用弧长法对已施加初始缺陷的模型进行非线性屈曲分析，得到构件的极限承载力。

1.4有限元模型验证受弯梁的整体稳定弹性临界弯矩公式[14]为

Mcr=β1π2EIyl2y×β2ea+β3βy+

β2ea+β3βy2+IωIy1+GItl2ωπ2EIω（1）

式中：E为弹性模量;G为剪切模量;ly和lω为梁长;Iy为弱轴惯性矩;Iω为翘曲常数;It为抗扭常数;ea为横向载荷作用点至剪心的距离;βy为截面不对称影响系数，双轴对称截面取0;β1、β2和β3均为经验参数，根据《铝合金结构设计规范》，本文取值分别为1.365、0.553、1.730。为验证有限元模型的正确性，采用式（1）计算A1系列构件的临界弯矩解析解，与有限元计算结果进行比较，见图6。两者平均误差为0.997，且大部分误差在3%以内，因此采用有限元按照特征值法求解梁弹性弯扭屈曲临界弯矩的方法可行且精度较高。为进一步验证有限元弹塑性结果的有效性，对文献[15]中的10个H形截面构件受弯试验进行分析，试件编号与文献中相同，构件的试验结果与有限元结果对比见表3。由此可知，构件承载力平均相差4.4%，失稳类型均为整体弯扭屈曲，与文献一致，说明本文有限元方法是可靠的，可以在此基础上展开参数分析。

2有限元参数分析为方便计算和使用，通常定义梁的整体弯扭屈曲稳定系数φb和梁整体稳定的相对长细比λp[12]分别为φb=MuMp（2）

λp=MpMcr（3）式中：Mp为梁截面的塑性铰弯矩，Mp=Wpf0.2;Wp为截面的塑性抗弯模量;Mu为梁的极限弯扭屈曲力矩;Mcr为理想受弯构件的弹性弯扭屈曲临界载荷。有限元计算结果表明，构件的破坏模式分为2种：一种是弯扭屈曲和畸变屈曲的耦合破坏（见图7），一种是整体弯扭屈曲破坏（见图8）。当构件长度较小时，由于板件较厚，卷边自由端与翼缘棱线发生畸变屈曲。构件越短，畸变屈曲控制作用越强，弯扭屈曲发展越不充分;当构件长度较大时，构件的破坏形式过渡到弯扭屈曲，截面形状基本保持不变，临近破坏时，面外位移增加较多，扭转变形加大。

2.1腹板高厚比的影响改变腹板的厚度和高度，即系列试件A1、A2、A3、B1和B2，研究不同长细比下腹板高厚比对构件稳定性的影响。腹板高厚比对构件整体稳定性的影响关系曲线见图9。

在腹板高度一定的条件下，极限弯矩随高厚比减小而增大。λp<0.9时，构件整体稳定系数提高，最大提高幅度为2.4%;λp>0.9时，构件整体稳定系数曲线基本重合。在腹板厚度一定時，构件极限弯矩随高厚比增大而增大，且效果显著，但构件稳定系数却减小。腹板高厚比越大，φb-λp曲线越低，说明腹板厚度对构件整体稳定的影响不大。同跨度下加大翼缘板的距离，其回转半径增大、长细比减小，从而承载力提高，但是在初始缺陷下，截面高度的增加使得构件更容易发生侧向屈曲破坏，导致其相对承载能力下降。构件的整体稳定系数大于1，是由材料应变强化引起的。铝合金材料截面具有非线性特征，长细比较小时抗侧刚度好，材料进入应变硬化阶段后，应力仍然持续增加，最终极限弯矩Mu大于塑性铰弯矩M[8]p。材料应变硬化参数n对铝合金受弯构件的稳定系数影响很大。6061-T6铝合金材料属于经过热处理加工后的弱硬化合金，不同的热处理方式对n的影响不同。当φb<1时，相同λp对应的φb随着n的增大而增大，而当φb>1时相反，相同λp对应的φb随着n值的增大而减小，这与文献[5]结果一致。