基于神经网络的裂纹扩展过程预测

郑国君 杜超群 申国哲 夏阳

摘要：  提出基于神经网络的裂纹扩展过程实时预测方法，其计算效率比近场动力学（peridynamic， PD）模型提高。使用PD算法获取裂纹扩展过程中的损伤云图，构建裂纹扩展数据集。基于数据集构建生成对抗网络（generative adversarial networks， GAN）模型，根据不同加载条件实时生成损伤云图，从而快速预测裂纹的扩展过程。将PD模型计算得到的损伤云图中的RGB值与相应位置处的损伤值结合，构建多层前馈神经网络模型的数据库，并使用多层前馈神经网络模型分析GAN模型产生的损伤云图，得到相应的损伤值。通过数值算例证明该方法的效率和准确性。

关键词：  近场动力学; 计算时间; 生成对抗网络; 裂纹扩展; 裂纹预测; 损伤云图; 前馈神经网络; 损伤值预测

中图分类号：  TP391.99; TB115.1文献标志码：  B

Prediction of crack propagation process

based on neural network

ZHENG Guojun， DU Chaoqun， SHEN Guozhe， XIA Yang

（State Key Laboratory of Structural Analysis for Industrial Equipment， School of Automotive Engineering，

Dalian University of Technology， Dalian 116024， Liaoning， China）

Abstract： A method of real-time prediction of the crack propagation process based on the neural network is proposed， and the calculation efficiency can be improved compared with peridynamic（PD） model. The damage contours of the crack propagation process are obtained using the PD model， and then the crack propagation dataset is built. Based on the dataset， the generative adversarial network（GAN） model is constructed. The damage contours are generated in real time according to differential loading conditions， thus the crack propagation process can be predicted quickly. The damage value database is built based on the RGB color values and the damage values at the corresponding position from the damage contours generated by the PD model. The damage contours generated by GAN model is analyzed using the multi-layer feedforward neural network model， and then the corresponding damage values are obtained. The efficiency and accuracy of the method are proved by numerical examples.

Key words： peridynamics; calculation time; generative adversarial network; crack propagation; crack prediction; damage contour; feedforward neural network; damage value prediction

收稿日期：  2021-08-16修回日期：  2021-10-21

基金項目：  国家自然科学基金（12072065）;中央高校基本科研业务费专项资金（DUT20JC34）

作者简介： 郑国君（1981—），男，湖北恩施人，副教授，研究方向为车身结构轻量化，（E-mail）gj_zheng@dlut.edu.cn

通信作者： 夏阳（1987—），男，河南驻马店人，副教授，研究方向为近场动力学等数值模拟方法，（E-mail）yangxia@dlut.edu.cn0引言经典连续介质力学是一种局部理论，其运动方程基于微分形式进行求解，当位移不连续时无法确定当前的运动方程，因此到目前为止依然难以通过连续介质力学对材料中裂纹的形成与扩展进行准确预测。SILLING等[1-4]提出非局部近场动力学（peridynamics，PD）理论，使用积分形式构建运动方程，实现材料在多部位萌生并沿任意路径进行扩展的计算。PD理论可以应用于线弹性、非线弹性、塑性、黏塑性以及黏弹性等[5-8]材料的行为，同时也可以应用于多晶材料[9]和复合材料[10]。PD理论的应用范围较广，但是计算过程较为复杂、仿真时间较长，且模型越大其计算复杂度越高，以目前计算机的计算能力无法实现实时的裂纹可视化仿真模拟和预测。人工智能、机器学习和大数据技术的发展，可为实现裂纹的实时可视化模拟和预测提供切实可行的方案。自GOODFELLOW等[11]提出生成对抗网络（generative adversarial networks， GAN）以来，由于GAN生成的图片效果好，吸引大量学者进行研究。借助GAN对输入响应迅速的优点，使用神经网络生成可视化的图片结果，可以实现对裂纹扩展过程的实时模拟。如RADFORD等[12]提出深度卷积GAN（deep convolutional GAN， DCGAN），使用反卷积层替代全连接层，可提升生成图像的质量;MIRZA等[13]提出条件GAN（condition GAN， CGAN），对GAN增加条件约束，使得生成结果更具有方向性;ARJOVSKY等[14]提出的WGAN（wasserstein GAN，WGAN）与GULRAJANI等[15]提出的WGAN-GP可改善GAN训练不稳定容易出现模型崩溃的现象，使得GAN的训练过程更加稳定;近年来ACGAN[16]、StackGAN[17]以及BigGAN[18]等结构的提出更是逐渐提升GAN的生成质量，同时也使得GAN获得更广泛的应用。在PD领域，KIM等[19]基于PD理论，使用卷积神经网络对受到撞击后磁盘的裂纹扩展结果进行预测，但是依旧需要后处理软件对生成结果进行可视化处理后才能观察裂纹的扩展情况。此外，NGUYEN等[20]通过神经网络拟合物质点的位移与施加载荷之间的线性关系，将机器学习与PD进行耦合，从而降低计算的时间消耗;计算包含4×104个物质点的模型时，可在每个时间步内降低约15%的时间消耗，但依旧难以实时得到可视化的裂纹扩展结果。本文使用PD算法对预制裂纹板在指定条件下进行仿真模拟，获取大量的损伤云图并构建数据集，使用该损伤云图数据集对基于图像数据驱动的GAN模型进行训练。基于该GAN模型，将载荷和加载时间步作为输入，在无须后处理软件的情况下，生成相应的预制裂纹板损伤云图，实现对裂纹扩展过程的实时可视化模拟和预测。同时，基于BP神经网络[21]拟合损伤云图的RGB颜色值与其相应的损伤值之间的函数关系，实现RGB颜色值信息到损伤值信息的预测。

1理论基础

1.1PD理论PD理论是一种非局部理论，在该理论中，物质粒子的位置对应材料的一个研究点，每个物质点有其各自的体积Vk和质量密度ρ（xk），通过物质点与其影响范围内所有物质点的相互作用，对物体的运动进行分析，该影响范围被称为“近场范围”。在PD中，假定物质点xk仅与其近场范围的物质点之间产生相互作用力，该力可以通过本构力函数f表示，PD物质点xk与xj之间的相互作用见图1。

PD物质点的空间坐标用xk和xj表示，相对应的物质点体积用Vk和Vj表示;物质点xk近场域范围的族用Hxk表示;近场域半径用δ表示。对此，SILLING[1]提出PD运动方程，该方程可通过牛顿第二定律推导得出，即ρ（x）u··（x，t）=∫Hxkf（u′-u，x′-x，t）dV′+b（x，t）（1）其离散形式为

ρku··k=Nj=1（fk，j（uj-uk，xj-xk，t））Vj+bk（2）

式中：ρk与Vk分别为物质点xk的密度与体积;uk与u··k分别为物质点xk的位移和加速度;N为物质点xk的数量;j为物质点xk近场域范围内除xk以外的物质点;Vj为物质点j的体积;fk，j为物质点xk与xj之间的相互作用力;bk为作用在物质点xk上的外力或体力密度。

1.2生成对抗网络GANGAN是一种新型的网络框架，由2个结构不同的多层感知机[22]组成，分别记为生成模型G和判别模型D。生成模型G记作函数G（z;θg），z为噪声，θg为生成模型参数。G（z;θg）可将噪声z映射到新的数据空间。判别模型则D记作D（x，θd），作为一个特殊的多层感知机，对x来自真实数据分布还是来自生成模型G的输出进行判断：x来自真实数据分布时D（x）=1，x来自生成模型G生成的数据分布时D（G（z））≈0。因此，GAN的优化过程是在“二人零和博弈”[23]中获得纳什均衡的过程。对GAN模型进行优化的公式为

minG （maxD V（D，G））=Ex～pdata（x）（log D（x））+

Ez～pz（x）（log（1-D（G（z））））（3）

式中：pdata（x）为在真实数据上x的分布;pz（x）为先验的输入噪声变量;E为期望。

2构建损伤云图预测网络数据集GAN模型需要图像数据作为驱动，因此需要通过数值算例得到损伤云图以构建数据集。本文使用PD理论对预制裂纹板进行仿真，构建损伤云图数据集。

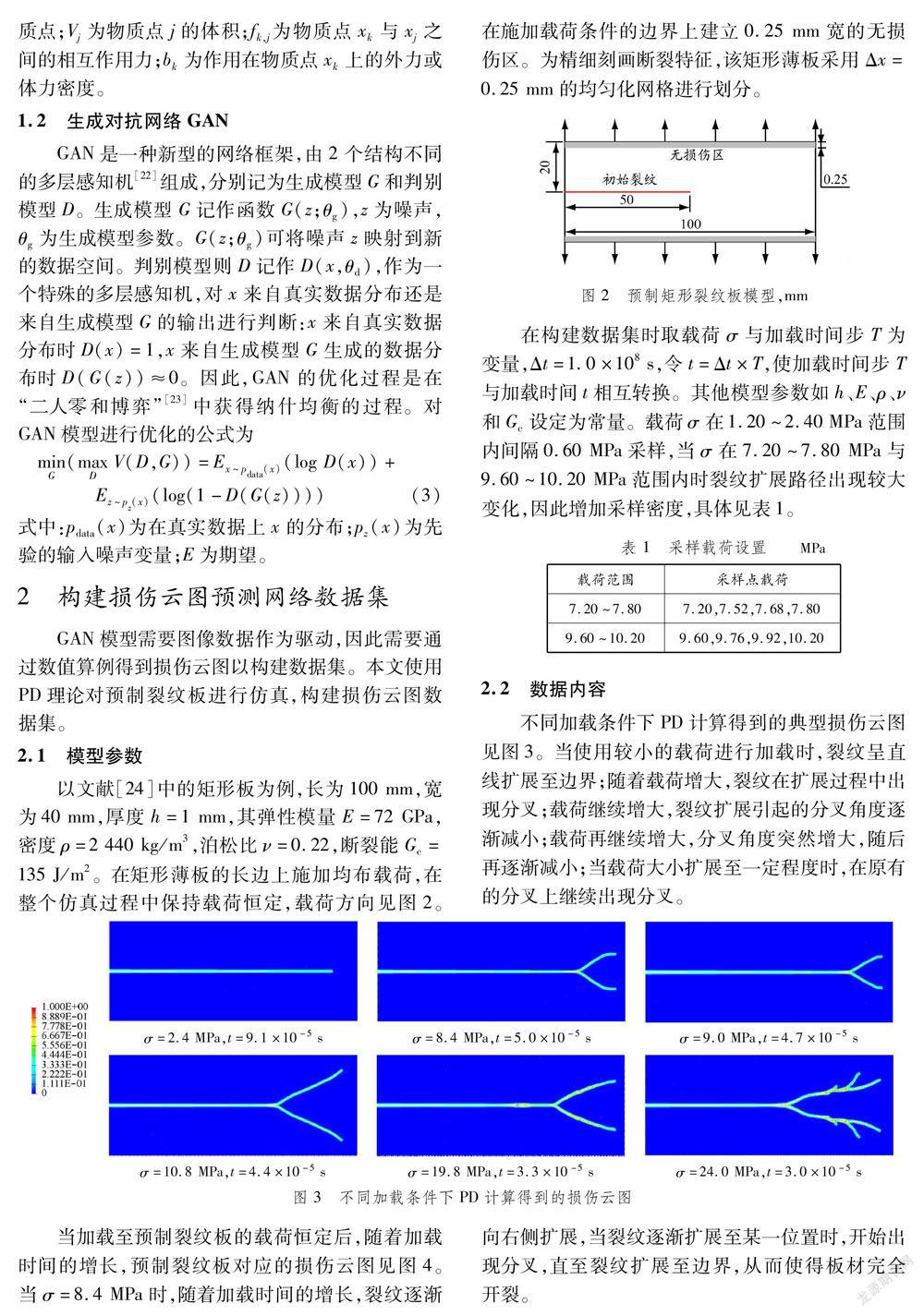
2.1模型参数以文献[24]中的矩形板为例，长为100 mm，宽为40 mm，厚度h=1 mm，其弹性模量E=72 GPa，密度ρ=2 440 kg/m3，泊松比ν=0.22，断裂能Gc=135 J/m2。在矩形薄板的长边上施加均布载荷，在整个仿真过程中保持载荷恒定，载荷方向见图2。在施加载荷条件的边界上建立0.25 mm宽的无损伤区。为精细刻画断裂特征，该矩形薄板采用Δx=0.25 mm的均匀化网格进行划分。

在构建数据集时取载荷σ與加载时间步T为变量，Δt=1.0×108 s，令t=Δt×T，使加载时间步T与加载时间t相互转换。其他模型参数如h、E、ρ、ν和Gc设定为常量。载荷σ在1.20～2.40 MPa范围内间隔0.60 MPa采样，当σ在7.20～7.80 MPa与 9.60～10.20 MPa范围内时裂纹扩展路径出现较大变化，因此增加采样密度，具体见表1。

2.2数据内容不同加载条件下PD计算得到的典型损伤云图见图3。当使用较小的载荷进行加载时，裂纹呈直线扩展至边界;随着载荷增大，裂纹在扩展过程中出现分叉;

当加载至预制裂纹板的载荷恒定后，随着加载时间的增长，预制裂纹板对应的损伤云图见图4。当σ=8.4 MPa时，随着加载时间的增长，裂纹逐渐向右侧扩展，当裂纹逐渐扩展至某一位置时，开始出现分叉，直至裂纹扩展至边界，从而使得板材完全开裂。

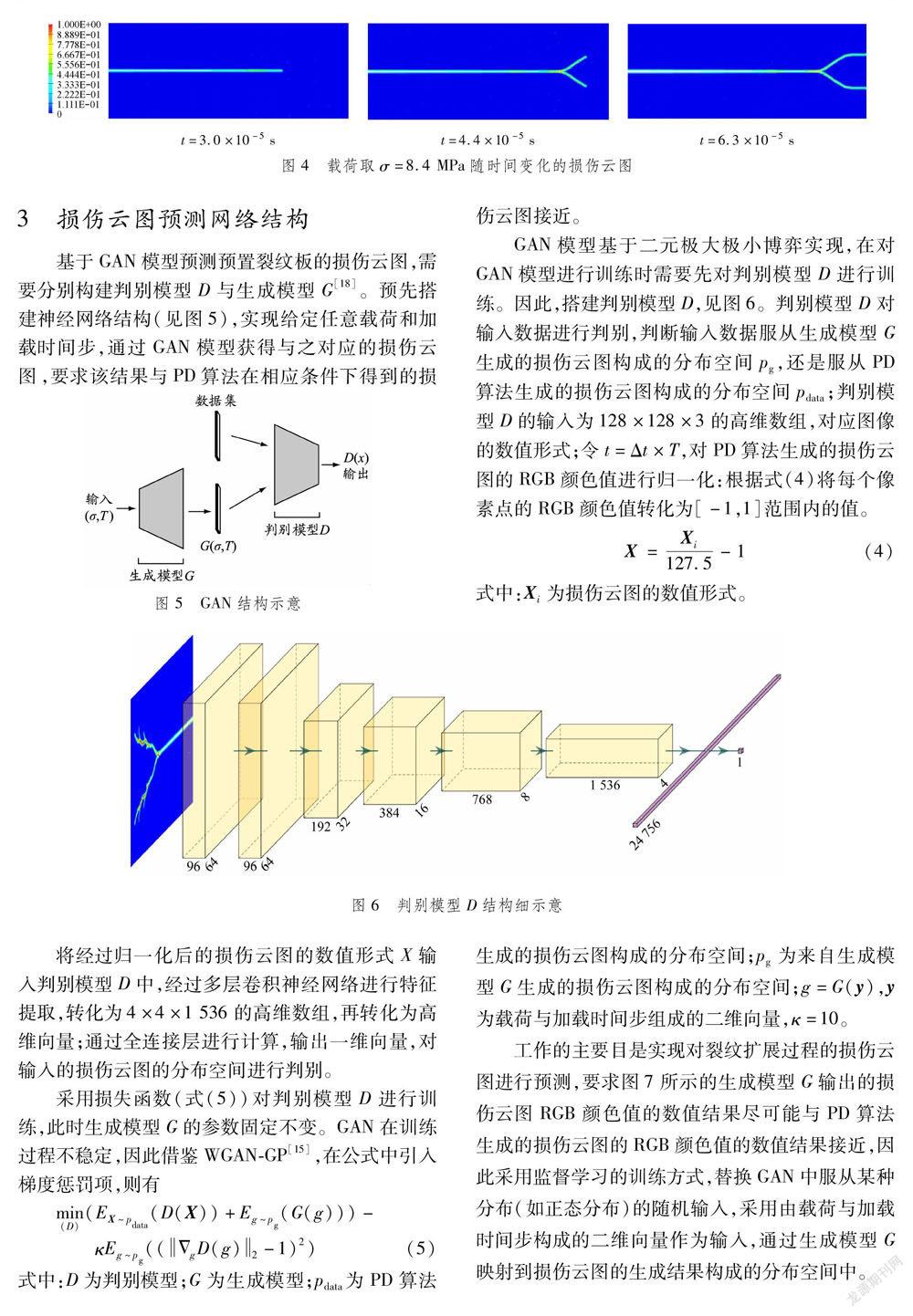
3损伤云图预测网络结构基于GAN模型预测预置裂纹板的损伤云图，需要分别构建判别模型D与生成模型G[18]。预先搭建神经网络结构（见图5），实现给定任意载荷和加载时间步，通过GAN模型获得与之对应的损伤云图，要求该结果与PD算法在相应条件下得到的损伤云图接近。

GAN模型基于二元极大极小博弈实现，在对GAN模型进行训练时需要先对判别模型D进行训练。因此，搭建判别模型D，见图6。判别模型D对输入数据进行判别，判断输入数据服从生成模型G生成的损伤云图构成的分布空间pg，还是服从PD算法生成的损伤云图构成的分布空间pdata;判别模型D的输入为128×128×3的高维数组，对应图像的数值形式;令t=Δt×T，对PD算法生成的损伤云图的RGB颜色值进行归一化：根据式（4）将每个像素点的RGB颜色值转化为[-1，1]范围内的值。X=Xi127.5-1（4）式中：Xi为损伤云图的数值形式。

将经过归一化后的损伤云图的数值形式X输入判别模型D中，经过多层卷积神经网络进行特征提取，转化为4×4×1 536的高维数组，再转化为高维向量;通过全连接层进行计算，输出一维向量，对输入的损伤云图的分布空间进行判别。采用损失函数（式（5））对判别模型D进行训练，此时生成模型G的参数固定不变。GAN在训练过程不稳定，因此借鉴WGAN-GP[15]，在公式中引入梯度惩罚项，则有

min（D）（EX～pdata（D（X））+Eg～pg（G（g）））-

κEg～pg（（ΔgD（g）2-1）2）（5）

式中：D为判别模型;G为生成模型;pdata为PD算法生成的损伤云图构成的分布空间;pg为来自生成模型G生成的损伤云图构成的分布空间;g=G（y），y为载荷与加载时间步组成的二维向量，κ=10。工作的主要目是实现对裂纹扩展过程的损伤云图进行预测，要求图7所示的生成模型G输出的损伤云图RGB颜色值的数值结果尽可能与PD算法生成的损伤云图的RGB颜色值的数值结果接近，因此采用监督学习的训练方式，替换GAN中服从某种分布（如正态分布）的随机输入，采用由载荷与加载时间步构成的二维向量作为输入，通过生成模型G映射到损伤云图的生成结果构成的分布空间中。

生成模型G的输入形式是由载荷与加载时间步构成的二维向量y，使用2层全连接神经网络对输入进行升维，转化为4×4×1 536大小的高维矩阵，经由多层反卷积网络计算，获得128×128×3的三维数组输出。基于式（6）将输入的二维向量进行归一化，转化为[0，1]范围内的值。y=yi-yi，minyi，max-yi，min（6）式中：i的取值为1和2;y1为施加的载荷;y1，min为最小载荷，y1，min=0;y1，max为最大载荷，y1，max=28.0 MPa;y2为加载时间步;y2，min为起始加载时间步，y2，min=0;y2，max为最大加载时间步，y2，max=12 000。仅使用GAN模型，无法实现生成模型G拟合载荷和时间步构成的分布空间与损伤云图构成的分布空间之间的映射关系，因此引入欧氏距离。在对生成模型G进行训练时，通过判别模型D指导生成模型G的结果，同时使用式（7）计算在同一载荷和加载时间步条件下，生成模型G获得的损伤云图与相应的通过PD算法得到的损伤云图之间的欧氏距离，即d=3z=1ni=1mj=1（xij，z-yij，z）2（7）式中：n与m分别为图像的宽和高，单位为像素;xij，z和yij，z分别为在图片数组中z通道ij位置的颜色值。欧氏距离坐标参考见图8。

使用损失函数（式（8）），基于Adam算法[25]对生成模型G进行优化，此时判别模型D的参数固定不变。

minG （EX～pdata（D（X））-Eg～pg（D（g））+λd）（8）

式中：λ为欧氏距离的权重系数。

4构建损伤值预测网络基于GAN模型实现损伤云图的预测，损伤云图只包含RGB颜色值信息，与图例比较可以确定其损伤值的范围，但是无法给出准确的数值结果。BP神经网[21]是一种基于误差逆向传播算法的多层前馈神经网络，通过系统性学习可具有优良的多维函数映射能力。基于BP神经网络，可通过输入损伤云图包含的RGB颜色值信息，输出相应的损伤值，实现基于BP神经网络拟合损伤云图RGB颜色值信息与损伤值之间的函数关系。

4.1数据集构建损伤云图由R、G、B等3个通道组成，分别对应红、绿、蓝3种颜色，每种颜色包含256级亮度，对应0～255范围内的整数。定义损伤云图中某一像素点的图像信息由三维向量xbp=[xRxGxB]表示，其中xR、xG、xB分别对应像素点R、G、B通道的颜色值。根据图例得到损伤值的范围为0～1，定义yd为该像素点处的损伤值。损伤云图可通过1 292×516×3的三维数组表示，具有1 292×516个像素点。以图像左上角点为原点建立坐标系，见图9。第i个像素点由坐标（xi，yi）定义。由于损伤云图裂纹区域具有丰富的颜色值信息，通过图像获取裂纹区域处的R、G、B颜色值信息，构建三维向量作为输入信息;使用HyperMesh获取该位置处相应的损伤值，作为监督信号，构成一组数据。对不同R、G、B颜色值采样，构建数据集。

4.2损伤值预测网络的搭建BP神经网络的输入层对应向量xbp的3个分量。搭建3层隐含层，每层包括10个神经元[27]。鉴于损伤值由0～1的数值表示，因此输出层的神经元个数取1。作为输入信息，xbp在输入神经网络之前用式（9）进行归一化处理。xin=xbp/255（9）在BP神经网络中，从隐含层到输出层之间每层神经元的输入为Ni，l=ni=1（wij，lxj，l-1）+bi，l（10）式中：Ni，l为第l层第i个神经元的输入;wij，l为第l-1层第j个神经元与第l层第i个神经元之间的加权系数;bi，l为第l层第i个神经元的偏置量。网络神经元的输出为hi，l=f（Ni，l）（11）式中：f（）为激活函数;hi，l为第l层第i个神经元的输出，BP网络共有5层，因此l取2～5。每个神经元取线性整流函数[28]作为激活函数，f（x）=max（0，x）（12）将式（13）作为损失函数，通过误差反向传播算法对BP神经网络进行权值修正计算。lo=（yd-hi，4）2（13）式中：y为监督信号;lo为损失函数值。

4.3损伤值预测结果分析取不在训练集内的8个采样点的RGB颜色值输入到BP神经网络中，与该点处实际损伤值进行比较，结果见表2。平均误差为0.561%，可见经过反复学习训练后的BP神经网络可以较好地拟合RGB颜色值与损伤值之间的函数关系。

5结果分析在不同载荷条件下，加载至t=5.0×10-5 s时，PD算法与GAN模型获得200张损伤云图的时间消耗结果对比见表4。其中，PD算法计算所需时间不包括使用后处理軟件转化为损伤云图所包含的时间。由此可知，GAN模型消耗的时间远低于PD算法所需要的时间。

为验证通过训练完成的GAN可以比较准确地预测0～24 MPa范围内任意载荷与加载时间对应的损伤云图，利用主观观察和数值对比2种方式进行验证。

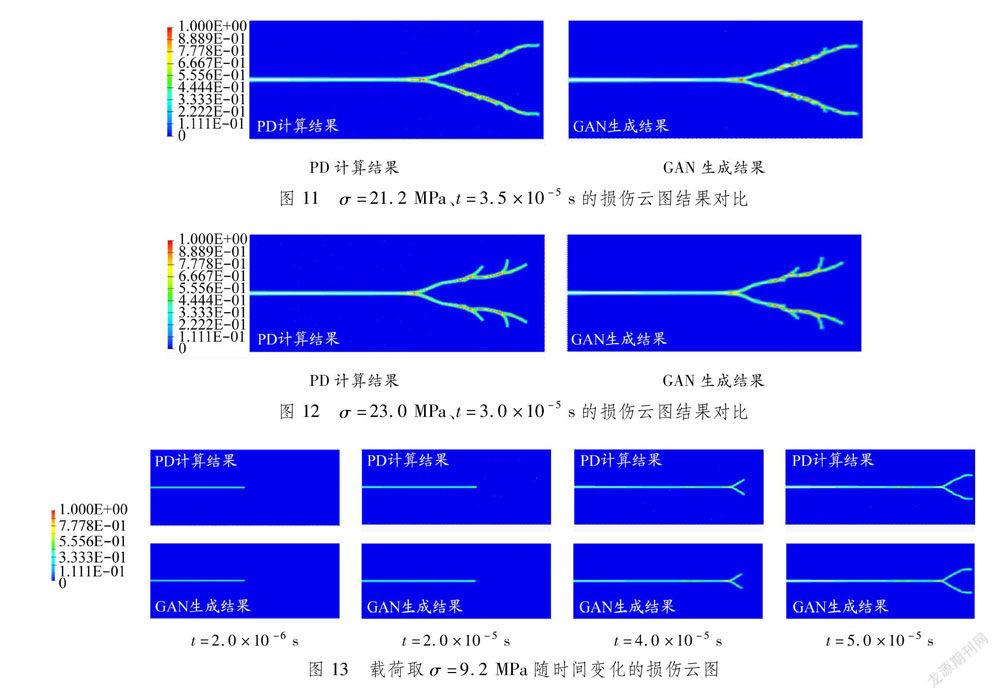
5.1损伤云图结果对比通过与PD算法获得的损伤云图结果进行主观对比，可以验证GAN模型生成结果的准确性。在载荷与加载时间分别为σ=14.8 MPa、t=3.8×10-5 s，σ=21.2 MPa、t=3.5×10-5 s与σ=23.0 MPa、t=3.0×10-5 s的条件下（该条件不在训练集内），GAN生成结果与PD计算结果损伤云图对比分别见图10～12。GAN模型与PD算法得到损伤云图裂纹出现分叉的位置和裂纹扩展的路径极为接近。因此可以认为，GAN模型能够根据载荷与加载时间预测相应的损伤云图。此外，σ=9.2 MPa时，改变加载时间，GAN模型得到的损伤云图与PD算法得到的结果对比见图13。在GAN模型得到的加载时间分别为t=2.0×10-6 s、t=2.0×10-5 s、t=4.0×10-5 s以及t=5.0×10-5 s的损伤云图中，裂纹长度和裂纹扩展的趋势与PD得到的结果极为接近，这也证明GAN模型具有预测裂纹扩展的形状随加载时间改变的效果。

5.2基于BP神經网络的结果对比由于损伤云图在输入GAN模型时由1 292×516×3的高维数组转化为128×128×3的低维数组，输出结果再由128×128×3转化为1 292×516×3，在转化过程中损伤云图损失大量的细节信息。当放大损伤云图（图14）时，相对于PD算法得到的损伤云图，GAN模型得到的损伤云图细节部分表现较为平滑，难以获得与PD一样的效果，但是依旧能确定损伤部分的大致轮廓，并通过图例确定损伤值的大致范围。

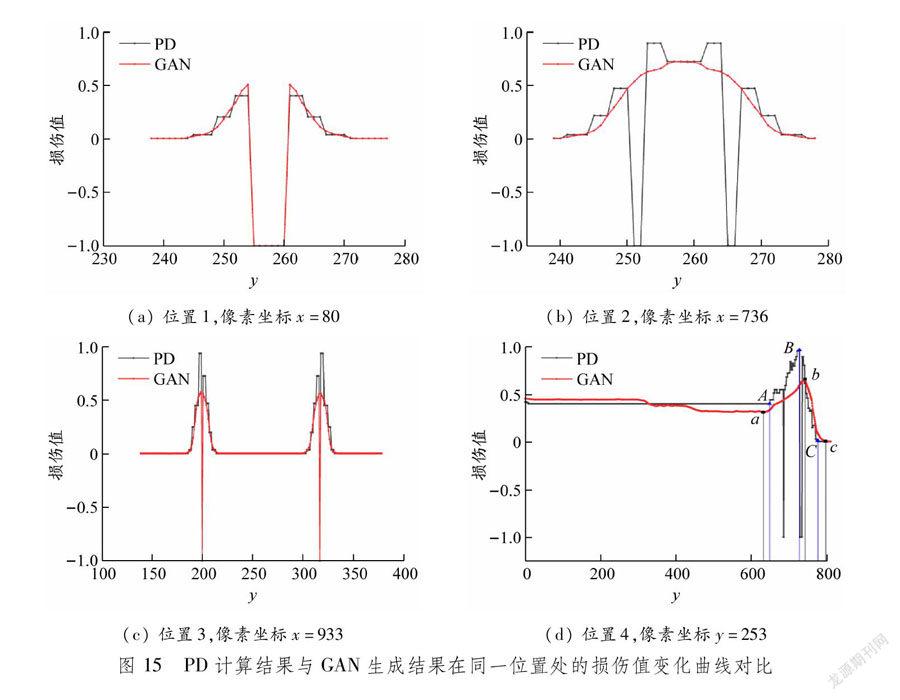
取σ=23.0 MPa、t=3.0×10-5 s条件下的损伤云图，使用所绘线段对应位置处的RGB颜色值，利用BP神经网络获取损伤值进行对比。白色区域代表无效区域，因此定义R、G、B各通道对应的颜色值≥220时的损伤值取-1，仍按图9建立坐标系。PD计算结果与GAN生成结果在同一位置处的损伤值变化曲线对比见图15。图14位置1、2、3的损伤值变化曲线横坐标与线段从上至下的像素点坐标对应。图15（a）为位置1对应的损伤值变化曲线图，图中PD对应的损伤值变化曲线呈阶梯式变化，线段上半部分损伤值逐渐增加，达到无效区域转变为-1，下半部分与上半部分关于线段的法线对称;GAN模型对应的损伤值变化曲线呈平滑的曲线状变化，其无效区域出现的位置与PD的结果重合。在位置2与位置3处，GAN模型与PD对应的损伤值变化曲线均关于线段的法线对称，且整体变化趋势相同，但当无效区域过小时，由于图像尺寸转化导致图像信息损失，GAN模型无法准确预测无效区域的位置，唯有增大GAN模型结构与输出尺寸才能获得与PD更为接近的预测结果。综上所述，可以认为GAN模型具有预测损伤值整体变化趋势的效用。

图15（d）为位置4对应的损伤值曲线，该线段具有810个像素点，与PD模型相比，GAN模型的损伤值变化曲线上升拐点a与PD模型中的上升拐点A相差17个像素点，其下降拐点b与PD模型的B点相比相差15个像素点，GAN模型中出现无损伤位置的拐点c点与PD模型的C点相差22个像素点，证明GAN预测得到的损伤云图中裂纹出现分叉的坐标位置与PD得到的结果接近，说明GAN模型对损伤值变化趋势的预测准确。

6结论基于GAN模型，通过PD算法获得损伤云图进行数据驱动，可实现在不同载荷与加载时间条件下对预制裂纹板的损伤云图进行实时模拟与预测。对比2种算法的计算消耗时间，证明GAN模型计算消耗的时间显著低于PD算法。分别对比2种算法在不同载荷与加载时间下的损伤云图，证明GAN模型的有效性与实时性。与传统PD算法相比，本文方法不仅可以显著提高损伤云图的生成速度，还可以脱离后处理软件，通过GAN模型实现损伤云图的实时可视化。同时，基于BP神经网络拟合RGB颜色值信息与损伤值之间的函数关系，实现通过损伤云图中的RGB颜色值到损伤值的预测。由于数据集的限制，仅能证明文中的方法能应用在少种类变量中，更多验证尚需要扩展数据集。神经网络对输入具有快速响应的能力，因此可将基于神经网络进行裂纹预测的方法应用于对目标对象的硬件状态实时检测与预测中，有利于提高目标对象的安全性。参考文献：

[1]SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. 2000， 48（1）： 175-209. DOI： 10.1016/S0022-5096（99）00029-0.

[2]SILLING S A， ASKARI E. A meshfree method based on peridynamic model of solid mechanics[J]. Computers & Structures， 2005， 83（17-18）： 1526-1535. DOI： 10.1016/j.compstruc.2004.11.026.

[3]SILLING S A， EPTON M， WECKNER O， et al. Peridynamic states and constitutive modeling[J]. Journal of Elasticity， 2007， 88（2）： 151-184. DOI： 10.1007/s10659-007-9125-1.

[4]SILLING S A， LEHOUCQ R B. Peridynamic theory of solid mechanics[J]. Advances in Applied Mechanics， 2010， 44： 73-168. DOI： 10.1016/s0065-2156（10）44002-8.

[5]KILIC B. Peridynamic theory for progressive failure prediction in homogeneous and heterogeneous materials[D]. Tucson： University of Arizona， 2008： 50.

[6]MADENCI E， OTERKUS S. Ordinary state-based peridynamics for plastic deformation according to VON MISES yield criteria with isotropic hardening[J]. Journal of Mechanics and Physics of Solids， 2016， 86： 192-219. DOI： 10.1016/j.jmps.2015.09.016.

[7]SILLING S A， BOBARU F. Peridynamic modeling of membranes and fibers[J]. International Journal of Non-Linear Mechanics， 2005， 40（2-3）： 395-409. DOI： 10.1016/j.ijnonlinmec.2004.08.004.

[8]ZHENG G， SHEN G， HU P， et al. Coupling approach of isogeometric analysis with non-ordinary state-based peridynamics[J]. European Journal of Mechanics： A/Solids， 2020， 82： 103981. DOI： 10.1016/j.euromechsol.2020.103981.

[9]DE MEO D， ZHU N， OTERKUS E. Peridynamic modeling of granular fracture in polycrystalline materials[J]. Journal of Engineering Materials and Technology， 2016， 138（4）： 16. DOI： 10.1115/1.4033634.

[10]ASKARI E， XU J， SILLING S. Peridynamic analysis of damage and failure in composites[C]//Proceedings of 44th AIAA Aerospace Sciences Meeting and Exhibit， 2006. Reno： AIAA. DOI： 10.2514/6.2006-88.

[11]GOODFELLOW I J， POUGET-ABADIE J， MIRZA M， et al. Generative adversarial nets[C]//Proceedings of 27th International Conference on Neural Information Processing Systems， 2014. Montreal： Association for Computing Machinery.

[12]RADFORD A， METZ L， CHINTALA S. Unsupervised representation learning with deep convolutional generative adversarial networks[EB/OL]. （2016-01-31）[2021-08-10]. https：//arxiv.org/abs/1511.06434v1.

[13]MIRZA M， OSINDERO S. Conditional generative adversarial nets[EB/OL]. （2014-11-30）[2021-08-10]. https：//arxiv.org/abs/1411.1784.

[14]ARJOVSKY M， CHINTALA S， BOTTOU L E. Wasserstein generative adversarial networks[C]//Proceedings of 34th International Conference on Machine Learning， 2017. Sydney： PMLR.

[15]GULRAJANI I， AHMED F， ARJOVSKY M， et al. Improved training of wasserstein GANs[EB/OL]. （2017-02-27）[2021-08-10]. https：//papers.nips.cc/paper/2017/file/892c3b1c6dccd52936e27cbd0ff683d6-Paper.pdf.

[16]ODENA A， OLAH C， SHLENS J. Conditional image synthesis with auxiliary classifier GANs[C]//Proceedings of 34th International Conference on Machine Learning， 2017. Sydney： PMLR.

[17]ZHANG H， XU T， LI H， et al. StackGAN（2017）： Text to photo-realistic image synthesis with stacked generative adversarial networks[C]//Proceedings of 2017 IEEE International Conference on Computer Vision. Venice： ICCV. DOI： 10.1109/iccv.2017.629.

[18]BROCK A， DONAHUE J， SIMONYAN K. Large scale GAN training for high fidelity natural image synthesis[EB/OL]. （2019-02-25）[2021-08-10]. https：//arxiv.org/abs/1809.11096？context=cs.LG.

[19]KIM M， WINOVICH N， LIN G， et al. Peri-net： Analysis of crack patterns using deep neural networks[J]. Journal of Peridynamics and Nonlocal Modeling， 2019， 1（2）： 131-142. DOI： 10.1007/s42102-019-00013-x.

[20]NGUYEN C T， OTERKUS S， OTERKUS E. A peridynamic-based machine learning model for one-dimensional and two-dimensional structures[EB/OL]. （2020-08-06）[2021-08-10]. https：//link.springer.com/article/10.1007/s00161-020-00905-0. DOI： 0.1007/s00161-020-00905-0.

[21]HECHT-NIELSEN R. Theory of backpropagation neural network[C]//Proceedings of International 1989 Joint Conference on Neural Networks. Washington： IEEE. DOI： 10.1109/IJCNN.1989.118638.

[22]PAL S K， MITRA S. Multilayer perceptron， fuzzy sets， classification[J]. IEEE Transactions on Neural Networks， 1992： 3（5）： 683-697. DOI： 10.1109/72.159058.

[23]MERTENS J-F， ZAMIR S. Value of two-person zero-sum repeated games with lack of information on both sides[J]. International Journal of Game Theory， 1971， 1（1）：39-64. DOI： 10.1007/BF01753433.

[24]BOWDEN F P， BRUNTON J H， FIELD J E， et al. Controlled fracture of brittle solids and interruption of electrical current[J]. Nature， 1967， 216： 38-42. DOI： 10.1038/216038a0.

[25]KINGMA D， BA J. Adam： A method for stochastic optimization[EB/OL]. （2014-12-22）[2021-08-10]. https：//arxiv.org/abs/1412.6980v5.

[26]HUANG G B， CHEN L， SIEW C. Universal approximation using incremental constructive feedforward networks with random hidden nodes[J]. IEEE Transactions on Neural Networks， 2006， 17（4）： 879-892. DOI： 10.1109/TNN.2006.875977.

[27]NAIR V， HINTON G E. Rectified linear units improve restricted Boltzmann machines[C]//Proceedings of 27th International Conference on International Conference on Machine Learning， 2010. Haifa： PMLR.（編辑武晓英）