二面角问题易错点透视

■安徽省太和中学 姜翠翠

本文通过对立体几何中有关二面角问题常见的易错题进行归纳总结，结合近几年全国卷中立体几何类题目的考向，帮助同学们纠正错误认识，提高正确解题能力。

一、不会建立适当的空间直角坐标系

例1（2020 年高考全国Ⅰ卷理）如图1，D 为圆锥的顶点，O 是圆锥底面圆的圆心，AE 为底面圆的直径，AE =AD。△ABC 是底面的内接正三角形，P 为DO 上一点，PO

图1

（1）证明：PA⊥平面PBC；

（2）求二面角B-PC-E 的余弦值。

解析：（1）设DO=a，由题设可得PO=因 此PA2+PB2=AB2，从 而PA ⊥PB。

又PA2+PC2=AC2，故PA⊥PC。所以PA⊥平面PBC。

图2

易错点分析：本题出错的原因主要有两个：一是不能合适地建系；二是C 点的坐标不会求或求错。题中未给出具体长度，需要指定单位长度。

小结：求二面角的大小的关键是作出二面角的平面角，然后构造三角形求解，即“一作二证三求”。向量法需利用空间直角坐标系，求两个平面法向量的夹角，再判断其与二面角平面角的关系。一般地，若设n，m 分别是平面α 与平面β 的法向量，则平面α 与平面β 所成的二面角θ 满足（当二面角为锐角或直角时）或cosθ=（当二面角为钝角时），其中锐角或钝角需根据图形确定。

二、二面角的正弦值和法向量夹角的余弦值之间的关系模糊不清

图3

例2（2020年高考天津卷）如图3，在三棱柱ABC-A1B1C1中，CC1⊥平面ABC，AC⊥BC，AC=BC=2，CC1=3，点D，E 分别在棱AA1和CC1上，AD=1，CE=2，M 为 棱A1B1的中点。

在外边飞着满天的大雪，我和翠姨坐着马车去买绒绳鞋。我们身上围着皮褥子，赶车的车夫高高地坐在车夫台上，摇晃着身子唱着沙哑的山歌：“喝咧咧……”耳边的风呜呜地啸着，从天上倾下来的大雪迷乱了我们的眼睛，远远的天隐在云雾里，我默默地祝福翠姨快快买到可爱的绒绳鞋，我从心里愿意她得救……

（1）求证：C1M ⊥B1D；

（2）求二面角B-B1E-D 的正弦值。

解析：依题意，以C 为坐标原点，CA，CB，CC1所在直线为x 轴，y 轴，z 轴，建立 如 图4所示的空间直角坐标系C-xyz，则C（0，0，0），A（2，0，0），B（0，2，0），C1（0，0，3），A1（2，0，3），B1（0，2，3），D（2，0，1），E（0，0，2），M（1，1，3）。

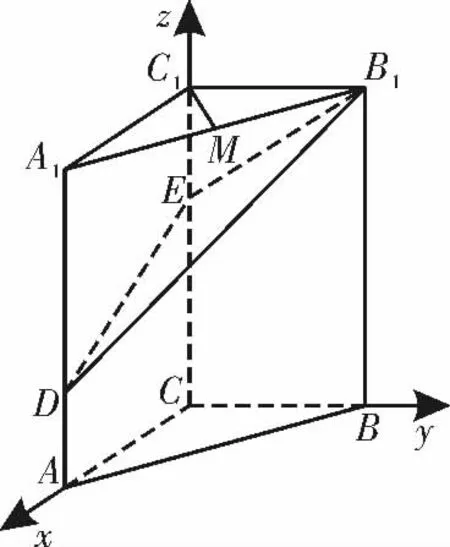
图4

三、不能作出二面角的平面角

例 3（2020 年六盘山高级中学高三（理））如图5，在四棱锥P-ABCD 中，PA ⊥平面ABCD，AD ∥BC，AD ⊥CD，且AD =

图5

（1）求证：AB⊥PC。

（2）在线段PD 上，是否存在一点M，使得二面角M-AC-D 的大小为45°? 如果存在，求BM 与平面MAC 所成角的正弦值；如果不存在，请说明理由。

解析：（1）由已知得四边形ABCD 是直角梯形。

又PA⊥平面ABCD，则PA⊥AB，所以AB⊥平面PAC，所以AB⊥PC。

（2）假设存在符合条件的点M。

如图6，过点M 作MN ⊥AD 于N，则MN∥PA，所以MN ⊥平面ABCD，所以MN⊥AC。

过点M 作MG ⊥ AC 于G，连接NG，则AC⊥平面MNG，所以AC⊥NG，即∠MGN 是二面角M-AC-D的平面角。

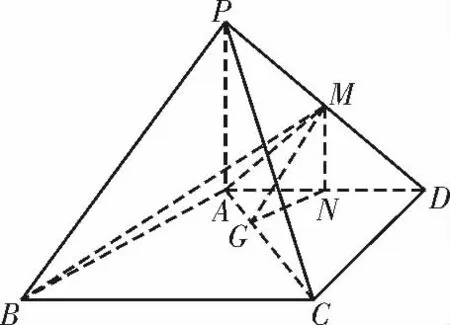
图6

易错点分析：本题出错的原因主要是不能准确作出二面角的平面角，依赖向量法解决二面角问题。

小结：本题属于探究性问题，已知二面角的大小，可先通过作辅助线，由线面垂直的性质定理找出二面角的平面角。也可以结合图形中的垂直关系建立空间直角坐标系，设出M 点的坐标，再利用向量夹角公式与二面角的余弦值建立等式关系求解。