基于数学核心素养视域谈初中几何教学

广东省广州市二中苏元实验学校(510000) 王碧莹

几何教学是初中数学教学的重要组成部分,在增强学生的基本技能、培养学生的逻辑思维能力、提高学生数学素养中担负着不可替代的作用.但是,几何难学是学生的心声,几何教学难提效是广大一线教师的苦恼,一条辅助线难倒一大片,千教万嘱难成效,几何成了学生数学学习的拦路虎.如何提高几何教学效率成了教师们关注的热点话题之一.笔者结合自身的教学实践,从数学核心素养的角度出发,探究提升初中几何教学效率的做法,以期抛砖引玉.

1 直观抽象互助力

几何是一门逻辑性十分严谨的学科,它的严谨性突出表现在几何语言的表述上.这给初中生的学习造成了不小的困惑,读起来朗朗上口,用起来一头雾水,归结起来就是太抽象.因此,在几何教学中,教师应有意识地运用直观手段,让学生在直观的情景中经历知识的产生和形成的过程,进而提升思维品质.同时,教学也应渗透抽象能力的培养,从直观经验中,抽象得出几何的元素,探究几何性质,丰富学生的感知,让几何知识在学生的学习中变得有血有肉.有直观参与的经历,有抽象而成的过程,直观抽象互助力,从而加深学生对知识的理解和运用.

1.1 案例1:“两条直线平行的判定”教学片断

活动1:

师: 同学们,我们刚学了两条直线平行的概念,你能够画出两条互相平行的直线吗?

学生基本都沿着尺子对边描出两条直线来.

师: 老师再考考你,大家先画一条直线a,在直线外任意画一个点P,你能够过点P画直线,让它与直线a平行吗?

学生独立思考尝试,同桌交流,教师引导学生一起参与,一步步画图,如图1 所示.

师: 反思刚才的画图过程,你有什么发现呢?

学生讨论,老师把学生的结论一一板书:

(1)只画出了一条直线;

(2)画出来的直线互相平行;

(3) 画图时直尺不动, 推动三角板移动.教师根据学生的发现进一步引导学生探究.

追问1: 你能用自己的语言描述发现(1)吗?

图1 画平行线图

生: 直线a和点P固定,只能画出一条直线与a平行.

追问2: 点P的位置有特别要求吗? 如果点P在直线a上,在直线a外,你画图的结果会怎样?

生: 点P在直线a外,可以画一条;点P在直线a上,画不出来.因此,点P在直线外是能够画出平行线的前提.

教师引导学生完成结论(1),并用数学语言表示出来.

平行公理过直线外一点,有且只有一条直线与已知直线平行.

追问3: 如果把“过直线外一点”这个条件去掉,你能画出几条直线与直线a平行呢? 同学们任意在直线外再找一个点Q,过Q再画直线a的平行线,你有何发现呢?

生: 过点Q又可以画一条,不要求过点P的话,可以画出很多条直线与直线a平行.

追问4: 这些直线有什么特征呢?

生: 互相平行.

师生归纳,得出平行传递性: 如果两条直线都与第三条直线平行,那么这两条直线互相平行.用符号语言描述为: 如果a//b,b//c,那么a//c.

追问5: 在画图过程中,三角板起到什么作用? 如果把直尺看成一条直线,你有什么发现?

生: 尺子看成一条直线l,三角板就是一个角,在画图中,直线l是截线,直线a,b是平行线,三角板形成的是同位角,在推动时,同位角不变.师生归纳,从画图中发现: 同位角不变,则画出来的直线互相平行.

活动2: 教师用几何画板画出任意两条直线a,b和截线c,标记一对同位角为∠1,∠2,并显示∠1,∠2 的度数,如图2所示.在此基础上,教师转动直线b,在转动的过程中,引导学生仔细观察直线a,b的位置和∠1,∠2 的度数变化.在几何画板的动态演示中,学生发现,当∠1,∠2 的度数相同时,两条直线a,b就平行,如图3 所示.

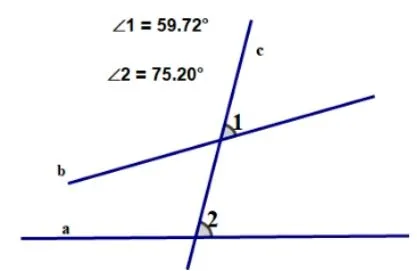
图2 同位角不相等图

图3 同位角相等图

活动3: 教师拿出教具:L型尺子和长方体木块,把尺子紧贴在木板,推动尺子,画出一条条直线,如图4 所示.引导学生观察画出来的图,你有什么发现吗?

生: 画出来的直线CD//EF.

师: 在画图中,尺子起到什么作用呢?

生: 尺子紧贴着木块,尺子与木块夹角90°,推动尺子的过程中,这些角都是同位角,都保持90°.

师: 同学们,从这几个活动中,你发现它们具有什么共同特点? 能用自己的语言描述这个发现吗?

学生讨论归纳: 只要同位角相等,两条直线就平行.

用数学语言表述,得到判定方法1: 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行.

平行公理、平行传递性、平行判定定理,这些都是学生学习平面几何的基础知识,之后的几何学习皆由此衍生.因此,对于这起始的知识要点,在教学中,我精心设计直观情景的教学活动,从动手画一画的亲身操作、几何画板具体数据的动态演示、用木匠工具画一画的直观体验中, 学生动手、动眼、动脑,积累直观经验,得出自然语言的结论.另一方面,在活动中教师引导学生把直观对象抽象成几何的点、线、面等,从直观思维上升到形象思维,再尝试用数学语言描述自己的发现,“冰冷”的几何不再是难以触摸,而是学生鲜活的实践和发现.

图4 木匠画平行图

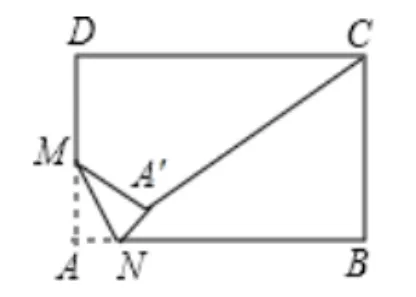
图5 案例2 图

2 动静结合总相宜

在初中几何教学中,教师要教给学生解决几何问题的策略和方法.在问题解决中,教师要暴露探究的思维过程,突破学生的解题难点,提炼通用的解题方法,让学生从解决具体问题的过程中学会怎样解题,习得处理问题的方法,提升数学能力.

2.1 案例2

如图5,在矩形ABCD中,AB=3,BC=2,M是AD边的中点,N是AB边上的动点,将∆AMN沿MN所在直线折叠,得到∆A′MN,连接A′C,则A′C的最小值是____.

在圆的教学中,我设计了这个问题.由于翻折、动点的问题一直是九年级刚开始学习圆知识时学生的难点之一,难处一是翻折前后图形的特征学生挖掘不到位, 二是由于点N是动点,此题∆AMN,∆A′MN都是动态图形,对翻折问题理解的难度更大.鉴于此,在教学中,教师采用搭“脚手架”的方式,引导学生从动中求定,通过定量、定点关系挖掘题目的不变量.在引导的过程中,让学生体验动静结合的妙用,克服面对动态图形的畏惧心理,提高学生的几何解决能力.教学片断如下:

师: 同学们先读题目,再独立思考(2 分钟),说说解决这题你的难处是什么?

生1: 点N是动点,除了题目的图形,还有很多种情况,我找不出方法.

生2: ∆AMN是动的,翻折后∆A′MN也是动的,点A′也是动的,很乱,我找不出A′C的求法.

师: 大家都觉得∆AMN的情况很多种,我们不防先以题目的图做参考,大家说说“将∆AMN沿MN所在直线折叠,得到∆A′MN”,从这句话你可能想到什么?

生3: 对应边相等, 对应角相等.AM=A′M,AN=A′N,∠AMN=∠A′MN,∠ANM=∠A′NM.

师: 这些关系式涉及的边角中,有固定的量吗?

生4: 有.AM=A′M=1,∠MAN=∠MA′N=90°.

师: ∠MAN= ∠MA′N= 90°, 那 么∠MAN+∠MA′N是多少呢? 它们还有什么关系吗?

生5: 互补.两个角相对,又互补,它们在一个圆上.

师生分析: 点A,M,N,A′都在同一个圆上,所以点A′虽在运动,但它是在以MN为直径的圆上运动,问题转化为求点C与圆上点连线段的最小值.分析至此,学生恍然大悟,接下来,教师放手给学生,让学生自己完成题目的解决.

在此题教学中,教师从学生的最近发展区入手,引导学生深读问题,迎“难”而上,从“翻折”的性质入手分析,引导学生由动变静,从而挖掘出点A′运动时保持不变的特性,借助隐圆解决问题.

2.2 案例3

如图6,四边形ACBD为⊙O内接四边形,AB为⊙O的直径,弦CD平分∠ACB,

(1)略;(2)若AC+BC=6,求CD的值.

师: 经过一番思考,大家说说从条件你会想到什么? 哪个条件难控制?

生1:“AB为⊙O的直径”暗示∠ACB,∠ADB都是直角.

生2:“弦CD平分∠ACB”暗示∠ACD= ∠BCD,AD=BD,D是半圆的中点.

生3: 我还发现了,∆ABD是等腰直角三角形.

生4:“AC+BC= 6”不好,AC,BC具体多长都不知道,题目中没有一条线段知长度.

师: 题目中不告诉我们线段长度,但6 是具体数字,我们能不能把6 和一条线段长度挂钩呢? 你有什么办法呢?

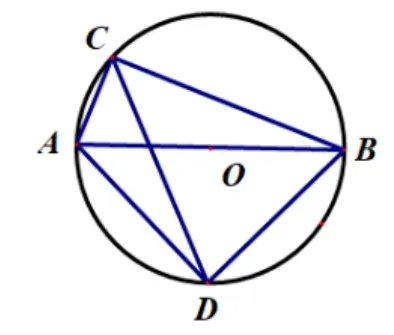
图6 案例3 图

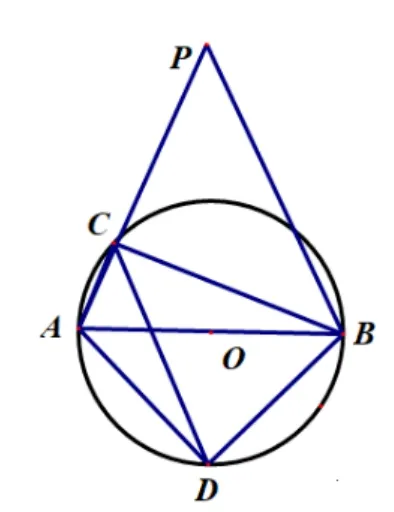
图7 学生5 探究图

生5: 可以把AC,BC移到一条直线上.我的作法是延长AC到点P, 使得CP=BC, 连接BP, 如图7 所示, 则AP= 6,∆PCB为等腰直角三角形,∆BCP与∆ABD相似.然后学生就说不下去了,发现没办法继续解决问题.

此时教师引导学生从同伴的探究中寻找新思路,从图7大家发现,其实∆BPC可以看成是由∆ABD绕点B又旋转又放大得到的,那么我们可以考虑用旋转来解决问题吗?图中有什么暗示我们可以用旋转呢?

生6: ∆ABD是等腰直角三角形, 可以支撑旋转.将∆ADC绕点D顺时针旋转90°得到∆BDQ,如图8 所示,则CD=DQ,AC=BQ, 易得∆CDQ是等腰直角三角形,由于圆内接四边形对角互补,因此点C,B,Q共线,所以CQ=6,DC=3.

问题解决后,教师再引导学生反思,题目中最有意思的是哪个信息? (D是半圆的中点),运用这个条件,你能自己编制一个题目考考老师和同学们吗?

在此题的解决过程中,教师从静态的图形,运用旋转的方法,让图形动起来,把分散的线段AC,CD集中在一条线上,从而化变量AC,CB为定量CQ= 6,动静结合,解决问题.既教给学生知识,又教给学生方法,教会学生思考.

图8 学生6 探究图

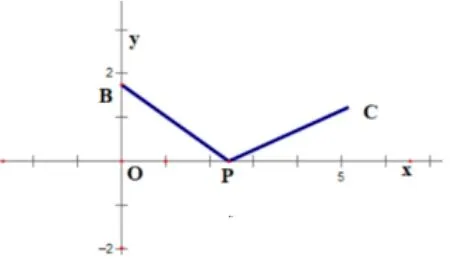
图9 案例4 图

3 数助形来相益彰

在几何教学中,教师要重视数学思想方法的落实,才能真正提高几何教学的质量,如数形结合思想,就是几何问题常用的数学思想方法之一.在几何中,用数助形,常起到意想不到的效果.

3.1 案例4

如图9,在平面直角坐标系中,点B坐标,P是x轴上一动点,将线段BP绕点P顺时针旋转120°后得到线段PC,则线段OC的最小值为____.

这是初三第一轮“三角形”复习时课堂上学生提出的题目,最后班上的学生都因为想不出解决方法产生了兴趣.本题的难处一是数据很少,二是由于点P在x轴上运动,可能在x正半轴,也可能在x负半轴,点C的位置也随着变化,可能在第一象限,也可能在别的象限,是否要分类讨论.我顺势引导学生利用这道题做一个几何思想方法的头脑风暴,先用特殊情况猜测点C的可能情况,再猜测内涵的归律寻找解决的方向.

师: 大家说这道题有哪些量是固定的?

生1: 点B,OB=∠BPC=120°,BP=CP.

师: 刚才的讨论中,同学们有什么想法呢?

生2: 我是想通过120°,60°这个条件来解决,但要怎么做我想不出来.

师: 同学们的想法都很好,下面我们站在同学们讨论的肩膀上,解决问题吧.

教师通过几何画板演示,生成点C的运动路线,如图10,学生观察发现点C的轨迹是一条直线.教师再引导学生如何画出这条直线,启发利用“两点确定一条直线”找特殊点的方法解决.

师: 怎么找60°角呢? 120°的补角就是60°, 比如∠BPO= 60°的话点C在哪? 120°的半角就是60°, 此时点C在哪? 坐标分别是什么?

生: 如图11, 当P1(1,0) 时∠BP1O= 60°, 此时点C1在x轴上,P1C1= 2;当P2(−1,0)时∠BP2O= 60°,此时点C2在y轴上,OP2=所以点C在直线C1C2上运动.问题转化为求点O与直线C1C2上点的连线段的最小值,运用面积法可解决.

图10 点C 的轨迹图

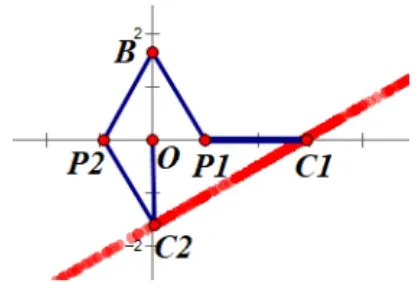
图11 特殊点定位图

由于初中学生的直观思维强但形象思维弱,因此,对运动点的问题教师运用归纳推理法,引导学生用特殊点的方法猜测结果,再解决问题.数学思想方法给学生几何学习插上思维的翅膀: 直观图(几何画板)——猜测——研究.虽然几何画板的图形生成带给了学生直观的依据,而初中生由于知识储备不够,也只能通过感知解决问题.但是,从理论上,这是不完全归纳法,还需理论支撑,此时,代数方法来助攻.

如图12,过点C作CH ⊥x轴于点H,设∠BPO=θ,则BP=∠CPH= 60° −θ, ∴化简得消元得∴点C的轨迹是一条直线.

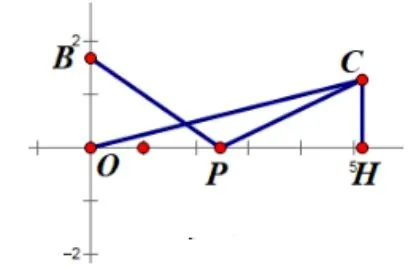
图12 代数法解决图

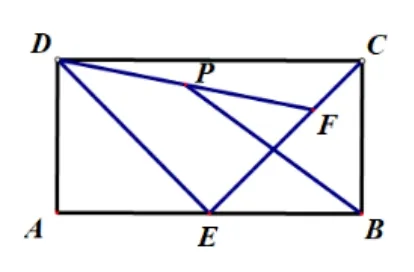
图13 案例5 图

3.2 案例5

如图13, 矩形ABCD中,AB= 4,AD= 2,E为AB的中点,F为EC上一动点,P为DF中点,连接BP,则BP的最小值是____.

在几何教学中应重视数学阅读的训练,教师在学生深读题目条件的基础上引导学生分析, 由于F是动点,DF,P,BP也是变化的,这是一个动态图形求最值的问题,执果索因,由于B点是固定,所以BP的最值要看P点的变化情况,即寻找P点的轨迹.

方法一: 几何法

探究1: 点P的运动有什么规律?

对初中学生来说直观想象比较擅长,所以教师从特殊点的角度引导学生发现点P的轨迹.

(1)当点F与C重合时,如图14 所示,P在P1处,此时P1是线段DC中点.

(2)当点F与E重合时,如图14 所示,P在P2处,此时P2是线段DE中点.

从图形可猜测,点P是在线段P1P2上运动,教师打开几何画板生成点P的轨迹,如图15 所示,验证学生的猜想.

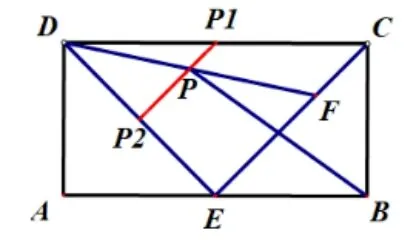
图14 特殊点定位图

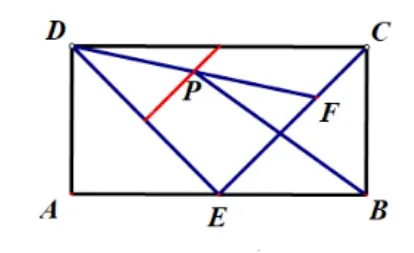
图15 点P 轨迹图

探究2: 为什么点P的轨迹是线段P1P2?

教师启发学生研究题目条件,最显眼的是“中点”,由此你想到了什么呢? 在此基础上,学生互相补充,在∆DCF中,点P,P1分别是DC,DF中点,∴PP1//CE,在∆DEF中,点P,P2分别是DF,DE中点,∴PP2//CE,由平行公理可得P,P1,P2三点共线,所以点P在线段P1P2上运动.

探究3: 如何解决问题?

∵AD= 2,AB= 4,E是AB中 点, ∴AE=BE= 2, 即∆ADE,∆BCE都是等腰直角三角形, ∴∠CEB= ∠DCE= 45°.∵P1,P2分别为DC,DE中点, ∴P1P2//EC, ∴ ∠DP1P2= 45°.∵P1是DC中点, ∴∆BCP1也是等腰直角三角形, ∴∠CP1B= 45°,∴∠BP1P2= 90°.即BP1⊥P1P2,∴BP1是BP的最小值,为

在解决问题时,教师启发学生从点F的运动情况,探究P点的轨迹,从特殊情况定点,猜测轨迹,再用几何画板直观验证猜测,最后从理论上证明猜测的正确性.教师带着学生经历“特殊情况——猜测——直观感知——推理论证”的几何研究过程,发展学生的思维,教会学生几何研究的方法,教会学生解决几何问题的策略.在问题解决后,教师再引导学生从代数的角度研究解决问题的方法.

方法二: 代数法

以点A为原点,AD所在直线为y轴,AB所在直线为x轴,建立平面直角坐标系,则D(0,2),B(4,0),设F(2+a,a)(0 ≤a≤2),则

方法1：由点P坐标可知点P在直线y=x上运动,∵DE:y=−x+2,∴DE ⊥P1P2,∴BP1⊥P1P2,故BP1的长是BP的最小值.

方 法 2:BP2=, ∴当a= 2 时BP取得最小值

4 基础知识应储备

几何基础知识是指几何的基本定义、基本定理法则、基本图形等.几何教学中,条理清晰、层次分明的规范推理表述,有赖于几何基础知识的储备;解决问题、分析思路有赖于基础知识的应用;深度掌握概念定理,甄别法则的区别与联系,有赖于基础知识、基本经验的经历和迁移.但是,在实际教学中,学生却不重视几何基础知识的积累,对概念、定理等觉得会背就可以.但是由于不理解,在应用时往往出现: 该用时想不起,用到时记不全,定理张冠李戴是常态.因此,教师要重视几何基础知识的教学、重视学生几何基础知识的储备,狠抓基础,为学生几何学习、研究提供理论支撑,让培养学生数学能力更好地落实在几何教学中,真正提升学生的数学素养.

比如,在菱形判定的教学中,学生经常觉得特殊四边形判定中最难的就是菱形,有的学生甚至用了三四次全等去证明,最后自己陷入逻辑“死循环”,耗时废力.

4.1 案例6

如图16, 在∆ABC中,AC=BC= 6, ∠ACB ＞90°, ∠ABC的平分线交AC于点D,E是AB上一点, 且BE=BC,CF//ED交BD于点F,连接EF.

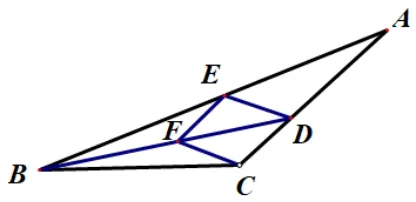
图16 案例6 图

(1)求证: 四边形CDEF是菱形;(2)略.

这是课堂上学生的自我检测题目,学生们都是用全等的方法,展示出来的成果如下:

∵BD平分∠ABC,∴∠ABD=∠CBD

在∆EBF和∆CBF中

∴∆EBF∽= ∆CBF(SAS)

∴∠EFB=∠CFB,EF=CF,∴∠EFD=∠CFD

在∆EFD和∆CFD中

∴∆EFD∽= ∆CFD(SAS)

∴DE=DC.

到这一步,因为有CF//ED,很多学生都想通过对边平行且相等的思路解决问题,但解决不了DE=CF,甚至有学生想作辅助线等,企图通过对角线关系来解决问题.其实题目至此,在平行的条件下,利用内错角相等及等腰三角形的性质,即可得到ED=EF,顺利解决问题.但是由于学生对基础知识储备不够,运用时不能流畅地接上,或者思维定势,从而错失了解决问题的机会.因此,在几何教学中,教师要注重几何基础知识的教学,舍得花功夫,舍得花时间,精心创设情景,让学生亲历知识产生的过程,“细嚼慢咽”,巧设探究,让学生丰富直观经验,厘清知识形成的来龙去脉,帮助学生建构知识框架,发展学生的思维.

“流水不腐,户枢不蠹”,几何教学是难教、难学,因为这不仅是教师教的问题,也是学生学习的问题.但是,教师们的不懈探究,同行们的思维碰撞,不停地给几何教学注入了源源不断的活水,带来几何教学有效性的提升.