基于核心素养“数学运算”的公式教学探究
——以“点到直线的距离”的教学为例
扬州大学附属中学(225002) 张 顺
《普通高中数学课程标准(2017 版)》中明确界定了数学学科的六大核心素养的内涵和水平划分.其中“数学运算”素养是指“在明确运算对象的基础上,依据运算法则解决数学问题的素养”,并从理解运算对象、掌握运算法则、探究运算思路和求得运算结果等方面给出了三个不同水平的划分.
基于数学核心素养之一“数学运算”的培养要求,近日,笔者在所教班级上了一节“点到直线的距离”的课.下面笔者就以此为例谈谈如何在数学课堂中的落实“数学运算”的培养.
1 教学内容和目标
1.1 教材分析
“点到直线的距离”是苏教版必修二第二章第6 节的内容,旨在解决“直线l:Ax+By+C=0 外一点P(x0,y0)到直线l的距离”.教材通过上节课已经证明的一道例题四边形ABCD为平行四边形,接着追问如何求平行四边形ABCD的面积,自然引到求点到直线的距离.教材对于该例题给出了两种解法“交点法”、“三角形面积法”,接着指出“交点法”计算量较大,“三角形面积法”计算简洁,再通过该方法求证出一般情形下“点到直线的距离公式”.
1.2 学情分析
高一第二学期学生在此之前已经学习了两条直线平行与垂直的判定、两点间距离公式和中点坐标公式等内容,已经具备了一定的利用代数方法解决几何问题的能力.“点到直线距离”小学、初中时就也就有所涉及例如求三角形面积时作出一边上的高,这个概念学生并不陌生,但学生由用尺规量出点到直线距离,上升到利用公式计算得到距离是思维层次的一大步提高.根据我所教班级学生特点学生素质较高,综合能力较强,同时由于是文科班女生占了绝大多数,学生代数运算,尤其是多字母的代数运算的能力还是不足的特点,本节课立足于提升学生的运算素养,尝试解释运算背后的算理,让学生能有所得.
1.3 教学目标
(1)通过点到直线距离公式的推导,渗透化归思想.
(2)通过点到直线距离公式推导的几种证法,使学生能理解算法选择的优劣,探究优化求解的思路,提升数学运算素养.
1.4 教学重难点
重点: 点到直线距离公式的推导;
难度: 对点到直线距离公式推导过程的优化.
2 教学过程
问题1:“点到直线距离”如何定义?
预设1: 过一点作已知直线的垂线,相交于垂足,点到垂足的距离为点到直线距离.
预设2: 已知点到直线上一点的最短距离为点到直线距离.
设计意图: 该问题一是让学生明白我们这节课所要研究的问题,二来通过该问题的两个预设为接下来推导点到直线距离公式的两种方法作铺垫.
问题2: 已知直线l:Ax+By+C= 0(A2+B2̸= 0)外一点P(x0,y0),求点P到直线l的距离?
预设1: 先求过点P垂直l的直线,再求两直线交点,最后用两点间距离公式.该方法可能遇到的问题: 学生不会求过点P与l垂直的直线;求不出交点;求不出两点间距离.
预设1: 先求过点P垂直l的直线,再求两直线交点,最后用两点间距离公式.该方法可能遇到的问题: 学生不会求过点P与l垂直的直线;求不出交点;求不出两点间距离.
设过点P与l垂直的直线为l′:Bx−Ay+D=0,由于过点P(x0,y0)故有Bx0−Ay0+D=0,将D=Ay0−Bx0代入l′得到l′:Bx −Ay+Ay0−Bx0=0 从而突破第一个难点.
最后再求两点距离:
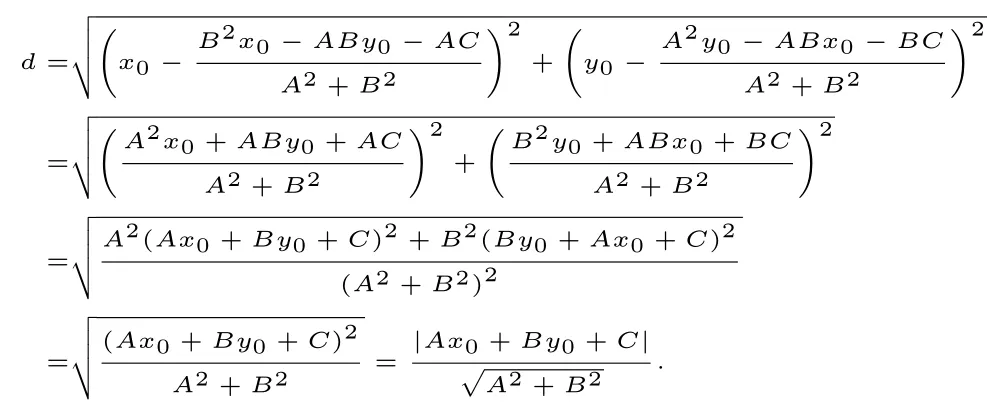
合理的进行通分合并同类项,学生运算中常见的问题是不考虑代数式得结构特征,“暴力”分解多项式从而破坏式子结构,而由于运能能力的不足,对于拆分后的式子往往没有办法更进一步的化简,使得计算难以进行下去.
追问1: 上面解法较为繁琐,计算容易出错,那么有没有更好的解法呢?
教师在黑板上板书如图(1) 所示图形, 提示学生要求PQ还能有什么方法.学生在图形提示下会联想到利用三角形面积求出PQ,于是有下面的解法.
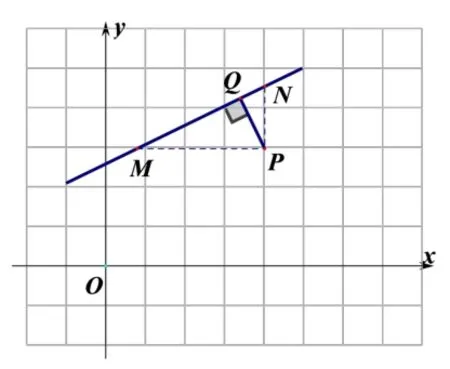
图(1)
设P(x0,y0), 则M(xM,y0),N(xN,y0) 代入直线方程解得同理NP=;因为所以
追问2: 为什么通过三角形等面积法转化后计算量会减少?
设计意图: 学生能看懂该解法,但是如果没有老师作图提示能主动联想通过三角形面积算两次得到斜高的学生应该不会很多.再者利用该方法为什么能起到简化运算的效果,是什么原因使然,对于这个问题学生想不到去追问,但这恰恰是比较重要的.通过转化与化归将求斜高转化为求两条平行于坐标轴的直角边长度,这种转化能简化运算的原因就在于其问题研究的坐标系是直角坐标系, 在直角坐标系中, 平行于坐标轴的两点距离是容易得到的|x1−x2|或者|y1−y2|,而在其它情况下会用到两点距离公式增加计算.
预设2: 学生会想到利用直线上一点与已知点求两者距离最小值来表示距离.
通过数学建模, 学生能建立直线上一点与已知点的函数关系式.设直线l上一点为Q(x,y), 定点P(x0,y0),于是PQ=由 于Q在 直 线l上,PQ最小时P,Q在与l垂直的直线上, 由预设(1)中解得的方程有计算时需要有目标意识, 需要我们求得的表达式结构中有(x −x0),(y −y0) 这两个量, 于是对上面方程组可以变形为又观察目标结构中有(x −x0)2+(y −y0)2,所以想到将方程组两式平方再相加,得到(A2+B2)[(x −x0)2+(y −y0)2] =(Ax0+By0+C)2, 最后得到
设计意图: 对于多字母运算学生在公式变形式往往像无头苍蝇到处乱撞,展开到哪里就到哪里.公式变形前没能对多要求的目标式的结构有所思考,另一方还需要学生公式变形时有一定的整体意识.这种方法学生不会那么容易想到,教学时需要教师一步步去引导,指导学生如何算,怎么想.
问题3: 前面探讨过通过构造三角形, 利用三角形面积来求高, 是否还有其他构造图形的方式?
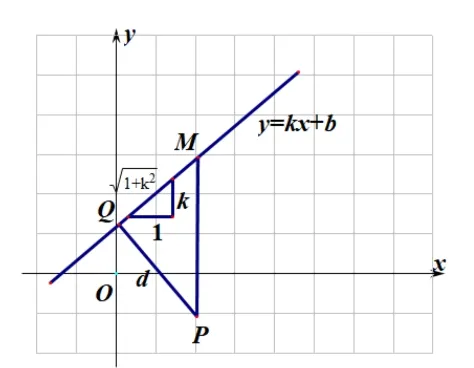
图(2)
教师板书如图(2) 所示图形,为了突出重点,这里只研究直线k存在且大于零情况.教师提示学生利用相似三角形知识.在老师的提示下学生能够得到大三角形MPQ与小直角三角形相似, 因为MP=|kx0+b −y0|,即, 最后再化为直线一般式下情形即可得证.
设计意图: 这种创造性的思维,教师预想的学生不可能构造出这种图形,所以需要板书出来直接给学生,学生通过这样的构造能体会到数形结合的思想,觉得数学美丽有趣就是成功!
3 小结
本节课用4 种方法证明了点到直线的距离: 交点法,面积法,构造函数法,构造相似图形法.交点法难算,但是解析几何证明题中少不了计算,当我们没有什么巧妙解法时,计算也许是唯一的路径,教学中也要让学生能有面对复杂计算能算下去的信心.面积法大大减少了计算,同学们也要对其背后原因有所了解,因为直角坐标系下平行于坐标轴的线段长度容易表示.构造函数的方法是本节课重点强调的一种方法,该方法首先要能准确建模构造出函数,列出目标表达式和约束条件,而求解最值化简过程中需要有整体思想和目标意识,时刻联想到所要求的的目标结构.最后为了提升学生学习数学兴趣,介绍了一种巧妙的构造相似三角形方法,讲解这种方法主要是让学生体会数学的美妙.

