面向飞腾处理器的高精度求和与点乘算法实现和优化*

黄 春，姜 浩，谷同祥，齐 进，刘文超

(1.国防科技大学计算机学院，湖南 长沙 410073；2.北京应用物理与计算数学研究所，北京 100088)

1 引言

近些年来，随着高性能计算机的不断发展，数值计算对于科学研究和社会应用越来越重要。规模巨大和运算能力强劲的计算机系统，被广泛应用于生物医疗、航空航天、人工智能、信息安全和气象预报等领域。高性能计算作为关键领域的核心技术，已经成为代表国家综合实力的科技要素之一。高性能计算技术的发展包括2个主要方面：硬件与软件。当前，计算机体系结构不断演进，新的计算硬件不断出现和优化。近年来国产处理器迅猛发展，在一定程度上实现了自主可控。飞腾处理器在自主研发微内核的基础上，实现了对 ARMv8 架构的兼容，其在较低的功耗下获得了较好的性能。

当前软件的发展和应用相对于国产硬件的发展还有很多需要提升的方面。高精度数学库的设计和实现，是解决大规模数值计算的可靠性和提升处理器性能的有效途径之一。线性代数数学库是高性能计算系统中最为基础的软件组件，因此研究线性代数数学库的高精度实现对发展高性能计算技术具有重要意义。经过近几十年的发展，目前比较广泛地用于科学计算的开源BLAS(Basic Linear Algebra Subroutine)库有GotoBLAS[1]、OpenBLAS[2]和ATLAS[3]等。其中，OpenBLAS是以GotoBLAS为基础，由中国科学院计算技术研究所张云泉和中国科学院软件研究所张先秩等人开发、维护的。OpenBLAS在多个平台上生成的代码性能比较优秀，因此本文选用OpenBLAS作为软件平台，实现高精度算法。

求和与点乘运算是数值计算中特别基础的组成部分，在大规模的线性代数计算中被频繁调用[4]。在现代科学计算中，需要处理的数据规模很庞大，而递归求和的舍入误差会随着数据规模n的增大而逐渐增加[5]，这就使得误差控制变得尤为重要。2005年，基于Knuth[6]、 Dekker[7]提出的补偿加法和乘法，日本早稻田大学的Oishi、Ogita和德国汉堡大学的Rump[8]提出了无误差变换(Error-Free Transformation)的概念，并设计了高精度的浮点数求和[8,9]及点乘[8]运算。2008 年，Yamanaka 等[10]设计了简单的高精度点乘运算的并行算法。2010年，香港科技大学的Lu 等[11]在GPU硬件加速平台上基于QD(Quad-Double library)设计了GQD(GPU-based Quad-Double library)高精度函数库。同年，日本筑波大学的Mukunoki等[12]在GPU上实现了BLAS 函数库4倍精度版本。日本理化研究所的Maho[13]基于QD library[14]及其它高精度软件库开发了高精度计算软件库Mpack，其针对BLAS 和LAPACK(Linear Algebra PACKage)实现了高精度的MBLAS(Modular Basic Linear Algebra Subroutine)和MLAPACK(Multiple precision Linear Algebra PACKage)。国防科技大学的Su等[15 - 17]在数学库的性能和精度方面做了大量工作。

本文利用无误差变换技术，结合飞腾处理器的硬件特点，实现并优化了高精度求和算法与点乘算法。应用本文设计的高精度算法，科研工作者可以进行更高精度的数值计算和模拟，对数值计算的舍入误差进行有效控制，从而使得计算结果的可靠性和稳定性得到进一步的保障。

2 理论背景简介

2.1 无误差变换

2005 年，Oishi等[8]提出了无误差变换的概念。设∘∈{+,-,×}，2个浮点数(a,b)∈F且有x=fl(a∘b)∈F，F为浮点数集合，在没有上下溢出，舍入模式为就近舍入时，存在:

(a∘b)=x+y

(1)

其中，x表示计算结果最好的浮点数近似，y∈F表示精确的舍入误差结果。满足上述表达式的过程即为一对浮点数加、减和乘法运算的无误差变换。无误差变换的基本原理是：在每次浮点操作的过程中，通过给定的计算方法计算出该次浮点操作产生的舍入误差，然后记录舍入误差，最终将累积的舍入误差补偿到浮点计算的结果中，属于误差补偿算法。

2个浮点数加法的无误差变换[6]如算法1所示。

算法1TwoSum

输入：a,b。

输出：x,y。

步骤1x=a+b；

步骤2z=x-a；

步骤3y=(a-(x-z))+(b-z)。

对于2个浮点数乘法的无误差变换，最为常用的是TwoProduct算法[7]，考虑到TwoProduct算法涉及浮点数分割操作，导致运算量比较大。并且，由于飞腾处理器的硬件可以直接支持混合乘加指令，结合硬件特点，本文使用基于混合乘加的乘法无误差变换TwoProductFMA算法[18]。TwoProductFMA算法如算法2所示。

算法2TwoProductFMA

输入：a,b。

输出：x,y。

步骤1x=a×b；

步骤2y=FMA(a,b,-x)。

2.2 基于无误差变换的高精度算法

基于无误差加法变换的高精度求和AccurateSum算法[8]如算法3所示。其中，步骤1是基于TwoSum算法循环对向量a的元素进行无误差求和变换；步骤2是对步骤1求和产生的舍入误差进行累加；步骤3将舍入误差补偿到最终结果。i和j表示向量a的下标索引。

算法3AccurateSum

输入：a。

输出：res。

步骤1 fori=2:n

[ai,ai-1]=TwoSum(ai,ai-1)；

步骤2 forj=1:n-1

temp=sum(aj)；

步骤3res=temp+an。

AccurateSum的相对误差界[8]为：

(2)

其中，eps=2-t，s为计算机中计算的结果，本文实验平台对应的t=64，γn=n·eps/(1-n·eps)，cond项表示求和向量中元素pi对应的条件数。

基于无误差加法变换和无误差乘法FMA变换的高精度点乘AccurateDot算法[8]如算法4所示。其中，步骤1使用了向量r存放舍入误差和计算结果，其长度2n是向量a长度的2倍；步骤2的循环中，第1个操作是使用TwoProductFMA算法计算向量元素相乘的结果和舍入误差，第2个操作是使用TwoSum算法将相乘得到的结果进行求和，得到求和的计算结果和舍入误差，结合循环计算，实现向量点乘的计算。步骤3和步骤4将点乘的计算结果和每次计算过程中产生的舍入误差相加，通过补偿的方式实现高精度算法。

算法4AccurateDot

输入：a,b。

输出：res。

步骤1[p,r1]=TwoProductFMA(a1,b1)；

步骤2 fori=2:n{

[h,ri]=TwoProductFMA(ai,bi)

[p,rn+i-1]=TwoSum(p,h)}；

步骤3r2n=p；

步骤4res=Sum(r)。

计算向量x,y的点乘时，AccurateDot的相对误差界[8]为：

(3)

其中，eps=2-t，t=64，γn=n·eps/(1-n·eps)，cond项表示点乘对应的条件数。

3 高精度算法的实现和性能优化

3.1 高精度算法的实现

由于高精度点乘和求和算法实现的思想类似，限于篇幅，以高精度求和算法的实现为例进行描述。高精度求和算法以加法的无误差变换为基础，对求和过程产生的浮点舍入误差进行循环补偿，从而实现精度的提高。AccurateSum算法的主要实现过程如图1所示。

Figure 1 Realization process of high precision summation图1 高精度求和实现的过程

图1中的ai表示求和输入的向量元素，ei表示每次求和产生的舍入误差，使用Sum_i对求和结果进行记录，最终将误差值与Sum_n相加，实现求和舍入误差的补偿。可以看到，AccurateSum算法以TwoSum算法作为核心，计算求和的值和舍入误差值。最终实现高精度求和的核心代码如下所示：

ld {v2.2d,v3.2d,v4.2d.v5.2d,[X]}

add X,X,#64

PRFM FLDL1KEEP,[X,#1024]

fadd v6.2d,v2.2d,v3.2d

fsub v14.2d,v6.2d,v2.2d

fsub v15.2d,v6.2d,v14.2d

fsub v16.2d,v2.2d,v15.2d

fsub v17.2d,v3.2d,v14.2d

fsub v10.2d,v16.2d,v17.2d

本文基于OpenBLAS软件实现高精度算法，通过新增函数接口的方式将实现的算法嵌入到库中，包含相应头文件即可直接调用。对于C语言和汇编实现的高精度算法分别添加了新增函数接口，如表1所示。

Table 1 New function interface表1 新增函数接口

表1中，函数接口名称中的“A”代表高精度实现，“C”和“S”分别表示使用C语言和汇编语言实现的算法。

3.2 性能优化

本文主要从寄存器分配、预取操作和循环优化等角度进行优化，采用手写汇编的方式实现核心部分，获得了较高的程序执行效率和较好的系统性能。飞腾处理器是基于ARM架构设计的，是load-store型的体系结构处理器,访问寄存器数据的速度要比访问存储器数据的快得多。为提高效率通常一次性进行多个字节的加载或存储，但同时也需要考虑寄存器数量的限制。为了尽可能地有效使用寄存器，对高精度算法进行了如下分析：高精度求和的核心为TwoSum算法，高精度点乘的核心为TwoSum算法和TwoProductFMA算法。TwoProductFMA算法和TwoSum算法的有向图如图2所示，其中变量a,b,x,y,z均为浮点数。

Figure 2 Directed graph of TwoProductFMA algorithm and TwoSum algorithm图2 TwoProductFMA算法和TwoSum算法的有向图

从图2可以看到，在不考虑寄存器复用的情况下，运行1次TwoProductFMA 算法需要4个寄存器，运行1次TwoSum算法需要8个寄存器。设Fn表示计算核的分块大小，对于计算核的4,8和16分块设计，不考虑寄存器复用时，所需要的寄存器数目N可以使用以下公式估计：对于高精度求和，N=Fn/4×8+Fn/4×6+2，而对于高精度点乘，N=2Fn/4×4+2Fn/4×6+3。具体结果如表2所示。

由表2可以知道，对于高精度求和，在不考虑寄存器复用的情况下，4分块设计会导致每次循环中有大量寄存器空闲；而16分块的设计则明显超出寄存器限制数目太多，即使考虑存放中间变量的寄存器进行复用，还是会有较大的寄存器资源竞争。8分块的设计，在理论上则较为合适，不会导致寄存器过多闲置，也能尽量避免寄存器资源限制导致的竞争。

Table 2 Number of registers required表2 寄存器需求数量

对于高精度点乘，在不考虑寄存器复用的情况下，16分块的设计明显会导致剧烈的寄存器资源竞争；4分块设计对寄存器利用不足；而8分块设计则超过限制数目，但考虑到实际计算过程中，串行计算部分的存在，存放中间变量的寄存器可以适当复用。因此，4分块的设计和8分块的设计都需要考虑，最终以实际测试效果作为选择依据。

将计算核做了分块后，程序设计的流程图如图3所示。

Figure 3 Flow chart of calculation kernel after partitioning图3 计算核分块设计后的流程图

考虑到每次循环中做了展开之后，循环计数值不是展开次数的倍数的情况，设计了F1计算核，每次取1个字数据进行计算，用于对小于展开次数的剩余数据进行计算。F8表示每次取8个字数据进行计算。

为了提高程序的性能，需要有效地命中Cache。对于核心数据，插入预取指令。在高精度算法的汇编实现中，使用PRFM预取指令对计算核心部分要用到的数据进行预取。对不同预取参数进行测试，得到的结果如表3所示。

Table 3 Test of time overhead to prefetch parameters表3 预取参数的时间开销测试

从表3可以看到，使用KEEP和STRM的效果没有明显差异，这是因为计算过程中取用的数据只用到1次，保持或者用完释放的效果没有明显差异。预取到L1中显然要比预取到L2中的效果好。出于一般性考虑，最终预取参数为：“PRFM PLDL1KEEP,[X,#1024]”。

4 数值实验与分析

本节所有的数值实验都是在 IEEE-754 标准[19]双精度下进行，计算使用的数据都是浮点数的形式。测试平台的配置如表4所示。

Table 4 Configuration of test platform表4 测试平台配置表

4.1 高精度求和算法的可靠性实验

进行求和数值实验的测试数据来自参考文献[8]，测试得到的结果如图4所示。图4中CommonSum表示普通的递归求和测试结果，AccurateSum表示高精度求和结果。

Figure 4 Relative error of summation with different condition numbers图4 不同条件数下求和的相对误差

从图4的测试结果可以看到，对病态数据求和时，高精度算法AccurateSum的精度比普通求和算法的精度要高。普通递归求和在测试数据的条件数增大到1015时，结果已经完全不可靠，而AccurateSum的结果仍较为良好，直到条件数增大到1030时才完全失效。测试结果表明，相较于普通求和算法，本文实现的高精度求和算法，有效地提高了求和计算精度。

4.2 高精度点乘算法的可靠性实验

在点乘测试的数值实验中，计算使用的测试数据来源于文献[8]。图5中的CommonDot表示普通的点乘结果，AccurateDot表示高精度点乘结果。

Figure 5 Relative error of dot product with different condition numbers图5 不同条件数下点乘的相对误差

从图5的测试结果可以看到，高精度算法AccurateDot的精度比普通的点乘算法的精度要高。普通的点乘在测试数据的条件数增大到1015时，结果已经完全不可靠。相较于普通的点乘结果，AccurateDot有更为良好的表现。测试结果表明，相较于普通的点乘算法，本文实现的高精度点乘算法有效地提高了点乘计算精度。

4.3 性能比较与分析

为了方便描述，使用不同的描述符号表示不同的算法实现方式，算法和描述符号的对照如表5所示。

(1)对普通求和算法和高精度求和算法的浮点运算量进行了分析，结果如表6所示。

Table 5 Comparison table of algorithm and description symbol表5 算法和描述符号对照表

Table 6 Analysis of floating-point operations in summation algorithms表6 求和算法浮点运算量分析表

从表6可以看到，进行普通求和的浮点运算量为1，而进行一次高精度求和的浮点运算量为7，从浮点运算量来看，高精度求和算法大致为普通求和算法的7倍。

(2)对高精度求和算法的不同实现进行了计算速度的测试，在不同数据规模下，以普通求和的汇编实现作为基准计算时间开销的比值，结果如图6所示。

Figure 6 Calculation time ratio of summation algorithms with different data scales图6 不同数据规模下求和算法的计算时间比

从图6可以看出，在不同数据规模下，SUM-A1的计算速度比SUM-A2和SUM-A3都快。进行统计平均之后，SUM-A1、SUM-A2和SUM-A3除以SUM-COM的平均时间比分别为1.76，3.32和7.35。这表明在使用3.3节所述的一系列性能优化策略之后，SUM-A1的计算速度得到了有效提升。结合处理器的硬件特点，对精度提高和计算速度实现了有效平衡。

(3)对普通点乘算法和高精度点乘算法的浮点运算量进行了分析，结果如表7所示。

Table 7 Analysis of floating-point operations in dot product algorithms表7 点乘算法运算量分析表

从表7可以看出，在使用FMA指令之后，进行一次普通点乘的浮点运算量为1，而高精度点乘算法的浮点运算量为11，从浮点运算量来看，高精度点乘算法大致为普通点乘算法的11倍。

(4)对高精度点乘算法的不同实现进行了计算速度的测试，在不同数据规模下，以普通点乘的汇编实现作为基准计算时间开销的比值，结果如图7所示。

Figure 7 Calculation time ratio of dot product algorithms with different data scales图7 不同数据规模下点乘算法的计算时间比

从图7可以看出，在不同数据规模下，DOT-A1的计算速度优于DOT-A2和DOT-A3的。进行统计平均之后，DOT-A1、DOT-A2和DOT-A3除以DOT-COM的平均时间比分别为1.57，4.65和7.70。这表明在使用3.3节所述的性能优化策略之后，DOT-A1的计算速度得到了有效提升。在精度提高和计算速度之间实现了有效的平衡。

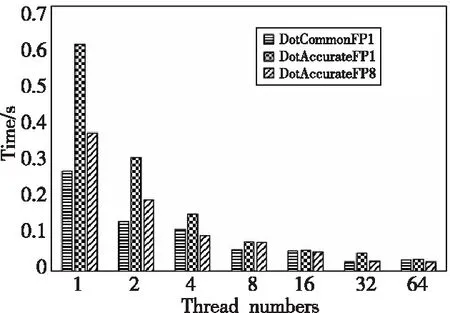
Figure 8 The change of calculation time of dot product algorithm with the number of threads图8 点乘算法计算时间随线程数目的变化

(5)对点乘的并行版本进行了测试，测试结果如图8所示。其中DotCommonPF1对应的是普通点乘的并行情况，实现内核为F1设计；DotAccuratePF1为高精度点乘并行计算的情况，使用的内核为F1设计；DotAccuratePF8为高精度点乘并行计算的情况，使用的内核为F8设计。

从图8可以看到，DotAccuratePF1为了提高精度，增加了计算量，总体计算速度比DotCommonPF1都要慢。在进行F8内核设计并进行优化之后，DotAccuratePF8的计算速度有了改善，甚至在某些线程并行情况下，计算速度比DotCommonPF1略快。从并行测试的情况来看，也再次表明优化策略是有效的。但是，由于此类带宽受限的算法在多线程并行实现过程中涉及归约操作，往往带来不可避免的Cache 缺失情况，因此多线程的扩展性不是很优秀。

综上所述，数值实验表明这类非计算密集型算法的瓶颈主要在带宽，因为高精度计算增加的额外计算量对于算法整体性能影响相对较小。

5 结束语

随着科学工程计算规模的增加、计算时程的增长，数值结果的精度可靠性越来越受到研究者的重视。对于国防安全等需求，如何在国产处理器上实现自主可控的软件至关重要。本文基于国产飞腾处理器，面向开源软件平台OpenBLAS，实现并优化了高精度求和算法与点乘算法。数值实验结果表明，虽然高精度算法增加了一定的浮点运算量，但计算结果的可靠性得到了进一步的保证，有效控制了浮点运算在大规模计算中舍入误差的累积。与此同时，结合国产飞腾处理器上的硬件特点，使用一系列性能优化策略，对计算精度和计算速度实现了有效的平衡。本文的工作可以用于提升大规模科学工程计算的稳定性和可靠性，以及为在国产自主可控处理器上实现自主可控软件提供了支持。对于算法实现的程序性能，可以在性能平衡上作进一步研究，以及以此为基础，对更上层的计算进行研究，为数学库的发展提供更多支持。