遗传算法在催化体系的全局结构优化中的应用

石向成，赵志坚，巩金龙

（1天津大学化工学院，绿色合成与转化教育部重点实验室，天津300072；2天津化学化工协同创新中心，天津300072；3天津大学-新加坡国立大学福州联合学院，福建福州350207）

引 言

物质通常以能量最低的状态存在，即基态结构(global minimum structure)，其能量处于势能面上的全局最小值点。对于催化体系而言，了解基态结构对于预测催化剂结构(如金属团簇体系)[1]、分析吸附特性(如吸附位点[2]、吸附结构[3]及表面生长过程[4])、研究多相催化反应机理[5-7]、认识反应物与催化剂的相互作用关系[8]、构建反应路径[9]、解释实验现象[10]等研究至关重要，并为催化剂的理性设计提供基础。基态结构是反应中最可能生成的结构[10]，但由于表征技术受限，通过实验观测基态结构的代价非常昂贵，所以理论模拟方法常被用以预测催化体系的基态结构。势能面具有高度复杂性和多维度性，并且随着原子数的增加，势能面上极小值点的数量以指数方式增加[11]。在现有计算条件下，通过遍历势能面上的所有结构来搜索基态结构，几乎不可能。所以，需要借助全局优化方法，实现在合理的计算时间内高效地搜寻催化体系势能面上的基态结构。

遗传算法(genetic algorithm)是一种基于自然选择机制的全局优化算法。它通过交叉、变异和选择等操作，模拟了自然淘汰进化过程，来搜索势能面上的基态结构。与其他基于单一的初始结构进行演化的算法(如盆地跳跃法、模拟退火法等)相比，遗传算法作为无偏(unbiased)优化算法，其优化效率及结果不受初始结构的影响[12]，具有很强的全局搜索能力。遗传算法尤其适合对体系的基态结构没有先验认知的优化问题。早在1993年，遗传算法就被成功用于Si4团簇的全局结构优化[13]。随后，Deaven等[14]引入了几何剪贴法(cut-and-splice pairing)，将交叉和变异等结构操作在实空间中得到了实现，并找到了C60团簇的基态结构，而模拟退火法并不能解决这一问题。在催化领域中，遗传算法已被应用于各种复杂的全局结构优化问题中，例如团簇体系[1,10,15]、表面吸附模型[16]、过渡态结构[17]、反应路径构建[6,18]等。近年来，通过引入并行计算、联用多种优化技术等方法而提出的改进遗传算法框架，降低了寻找基态结构所需要的计算成本，并提高了优化效果。如Hartke[19]引入“小生态环境”(niches)改进的遗传算法，就可以找到标准遗传算法所不能找到的LJ75团簇的基态结构。而在不断发展过程中，一批成熟的、针对特定问题而开发的遗传算法程序也被提出、改进和应用，例如晶体结构预测程序USPEX[20]、团簇体系优化程序BPGA[21]等。

在大数据时代下，遗传算法可以无偏地生成个体结构[17]，为机器学习提供训练数据，以此来构建结构与能量的构效关系，帮助设计高效催化剂材料[22-23]。而在遗传算法优化过程中，昂贵的能量计算可以被机器学习模型所取代，在保证计算精度的前提下，近百倍地提高优化性能[24]。未来，遗传算法将继续向并行化(充分利用计算资源)、智能化(使用机器学习方法降低不必要的高精度计算次数)、通用化(能处理各类复杂的体系)的方向发展，加快优化速度，以较少的计算代价获得基态结构。

本文主要针对遗传算法在催化体系中的全局结构优化技术进行了讨论，首先介绍了用于全局结构优化的遗传算法的基本程序框架，并综述了近年来为提高结构优化效率而发展出的改进框架，结合了相关应用实例进行说明，为遗传算法的进一步改进以及更广泛的应用提供理论指导。但由于篇幅有限，且不同优化问题的程序框架差别较大，涉及催化体系中的参数优化问题，如反应器设计、反应条件优化等，非本文讨论重点。

1 遗传算法的基本框架

目前在实空间中对催化体系进行全局结构优化的遗传算法，基本沿用Deaven 等[14]设计的框架。除了基于原子坐标，基因编码亦可以作为遗传算子[25]，即完全模拟基因遗传的过程，将待优化的信息(如原子坐标)进行编码(如二进制编码)，然后在编码层面上进行交叉、变异，生成子代。但在基因编码过程中，能量较低的结构特征很容易遭到遗失，并难以在生成子代时得以保留。并且，编码方式的选择也会对优化效率造成影响[26]，选择不恰当的编码方式可能会降低优化效率[27]。而Deaven 等设计的遗传算法框架是基于原子坐标进行交叉和变异等结构操作，所以能很好地保留低能量的结构特征，并将其从父代传递到子代[10]。即便由于体系过于复杂而难以得到基态结构时，也可以通过分析优化过程中出现的低能量结构特征，得到部分结论[2]。本文主要介绍在实空间中进行结构优化的遗传算法框架。

1.1 结构初始化

遗传算法在优化中不依赖于输入结构，其初始种群通常是随机产生。最简单的方式是在一定空间区域内随机位置放置原子来生成初始种群。为了保证结构合理性、减少不必要的计算负担，需要对原子间距进行限制，防止出现原子分布过于零散或过于紧密的情况。一般以两原子间的共价键长为标尺，设定原子间的最短距离及最长距离。不符合距离要求的结构将会被拒绝。初始种群的个体数量并没有严格的限制，但初始种群的数量越多，结构多样性越丰富，则越有利于提高遗传算法的优化效率。而每代的个体数量对优化性能同样有所影响[28]。

基于对基态结构的先验认知，在初始种群生成时引入限制条件，使个体尽可能生成在最优解可能存在的范围内，可以提高初始种群的质量。例如，对于晶体结构而言，除了原子坐标，晶格参数也可以用来描述其结构特征。通过结合空间群特征，将生成的原子随机放置在Wyckoff 位置上，并进行对称性操作，生成带有对称性的初始种群，能提高初始种群中能量较低结构的比例，减少搜索空间和优化参数，提高优化效率。如图1 所示，Lv 等[29]分别以38 和100 个原子Lennard-Jones 团簇(LJ38和LJ100)为例进行了测试。结果表明，在引入对称性限制以后，结构整体的能量分布明显地向能量较低的区域进行了移动。相似的结果也在Lyakhov 等[30]和Wang等[31]的工作中得到报道。除了对对称性进行限制，Zhai 等[32]则从键长入手，发现基态结构的键长基本服从一个均值接近共价键长的正态分布。当种群初始化时，可以要求个体的键长服从正态分布，使生成的结构更加合理。

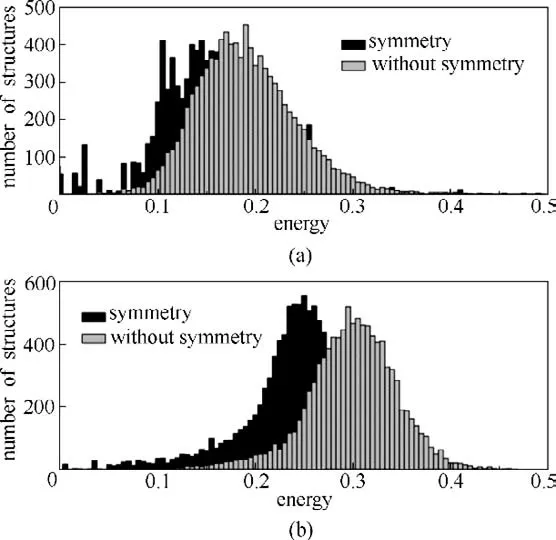
图1 包含和不包含对称性时随机产生的LJ38(a)和LJ100(b)团簇的能量分布（能量值是相对基态结构的相对值）[29]Fig.1 Energetic distributions of randomly generated structures for LJ38(a)and LJ100(b)clusters with and without symmetry（energies are shown relative to the global minimum）[29]

所有新生成的结构都需要进行局部优化[30]。根据优化问题的不同，可以使用经验势函数、密度泛函或量子Monte Carlo 等方法进行优化。但作为群体搜索方法，遗传算法需要迭代多次，对大量候选结构进行能量评估[33]，才能发现基态结构，计算量较大。所以对于原子数较多的复杂体系，很难使用精度较高的密度泛函方法进行，通常使用经验势函数进行[34]，如Lennard-Jones势函数、Gupta势函数等。

1.2 适应度及自然选择

个体的适应度(fitness)与优化问题中的目标函数值相关。不同优化问题所选取的目标函数值也不同。如果以找到势能面上的基态结构为优化目标，通常取热力学数值作为目标函数值。

对于一个优化问题而言，如果其目标函数值的范围已知，可以将目标函数值作为绝对适应度(absolute fitness)进行衡量。但对大多数结构优化问题而言，热力学数值的范围并不可知，所以应采取动态适应度方法，即个体的适应度值取决于其所在种群中最优个体和最差个体的目标函数值，并仅在同一代中衡量不同个体结构的适应度[1]。根据优化问题的不同，适应度的计算公式有所不同，一个基于能量的常用公式如式(1)所示[35]：

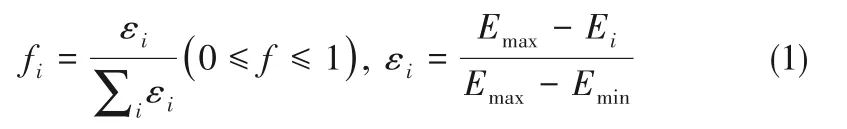
其中，fi和Ei分别为每代中每个个体的适应度和能量，Emax和Emin分别为此代中所有结构的最高能量和最低能量。

优化问题也可以有多个目标函数值，例如Maldonis 等[36]基于遗传算法，开发了用于构建与实验数据相吻合的复杂纳米体系的多目标全局优化算法，在优化过程中，不仅要求结构的能量趋于稳定，亦要求结构的模拟电镜谱图与实验数据吻合良好。但是，这类多目标优化问题通常需要在多目标下选取折中方案。正如帕累托最优理论表明，提升一个目标函数值，必然损害另一个目标的达成[25]。可以使用多目标遗传算法对这类问题进行优化，如非支配排序遗传算法Ⅱ(NSGA-Ⅱ)[37]和强度帕累托进化算法2(SPEA2)[26]。

自然选择模拟了生物进化中的“适者生存”，按照适应度选择父代，进行交叉生成子代。常见的选择方法[38]有轮盘赌选择法(roulette wheel selection)和锦标赛选择法(tournament selection)，其核心思路均是根据每代个体的适应度，按概率选出父代，适应度越高，则被选中的概率也越大。如果直接选择适应度靠前的若干个体作为下一代，会损害优化过程中的结构多样性，最终导致“早熟”现象，即优化过程过早陷入局部极值[39]。

1.3 交叉及变异

交叉(crossover)是根据父代的结构信息来构造新的子代结构的过程。交叉使优良基因得以从父代遗传至子代，是遗传算法中最重要的一步[16]。目前使用的交叉方法思路基本沿用Deaven 等的几何剪贴法，并在不同优化问题中有不同的形式。其基本思路如图2(a)所示，通过划定一个空间面，将父代的结构分为两部分，然后分别取两个父代的部分结构，并确保前后原子数目、化学计量比保持一致且原子间距合理，组成一个新的子代。另外，切割面也可以为非平面，图2(b)的例子展示了使用环切面进行交叉，形成新子代的过程[33]。

一般选取两个父代进行交叉，但也有使用单个或多个父代进行交叉的报道。2000 年，Rata 等[40]提出了单母体遗传算法，并用于带不同电荷的Si13到Si23团簇的全局结构优化，成功得到比之前报道能量更低的团簇结构。单母体遗传算法只需剪切和组合运算，不需要考虑团簇中原子的个数与比例。Jäger 等[41]则在几何剪贴法的基础上，发展出了三母体的交叉算子，用以进一步增加种群中的结构多样性。

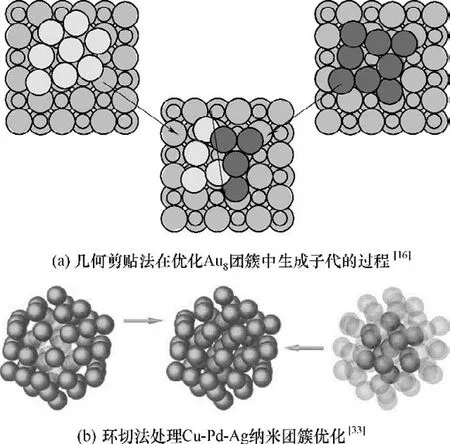
图2 父代通过几何剪贴法交叉形成新子代的过程Fig.2 The cut-and-splice pairing used on the crossover process for the generation of new structure

但交叉仅是将已有的基因材料混合，并未产生新的基因材料。单纯依赖交叉生成新结构，不利于结构多样性。所以，需要引入变异(mutation)机制，对现有结构进行调整，产生新结构，引入新的基因材料。一般按比例选取部分交叉后的结构进行变异。常见的变异操作有移动(rattle，选取部分原子发生随机位移)、置换(permutation，选取部分不同类型的原子交换位置)、对映(mirror，划定一个过质心的空间面，选取某一边的所有原子旋转180度)等[16]。

另外，为保证结构多样性，需要对新生成的结构进行相似性检测，避免生成与现有个体相似的结构[42]。通常是通过基于原子间距离的办法来判断结构的相似性[16]。Wang 等[31]通过构建成键特征矩阵，涵括了键长、键角和成键种类，能够更全面反映结构的所有成键信息，避免相似结构的生成。

遗传算法的收敛标准依照实际优化问题以及所使用的遗传算法框架的不同而各有不同。常见的收敛标准有[43]：(1)设定执行优化的代数，迭代达到指定代数后停止优化；(2)设定最优结构的期待能量值，当出现某一结构的能量达到预值时，停止优化；(3)当最优结构的能量在多次迭代后基本不变或变化不大，停止优化。

2 遗传算法程序的改进设计

在Deaven 等[14]所设计的遗传算法框架的基础上，为了提升优化效率，近年来亦有许多改进的遗传算法框架的报道。主要方式包括引入并行计算、机器学习等技术，充分利用计算资源，降低不必要的高精度计算次数，在更短的时间以更高的效率找到基态结构。

2.1 并行式遗传算法

遗传算法通常是基于逐代演化。每代生成数个结构后，再进入下一代。但由于不同结构的生成、计算时间不同，每代的运算时间总受限于其中运算速度最慢的结构。所以，有必要引入并行计算，充分利用计算资源，加快运行速度。目前在遗传算法中，主要的并行方式有两种[43]：(1)并行生成子代结构及进行能量计算；(2)并行运行多个相互独立的遗传算法优化。

一个典型的并行式遗传算法的例子是Shayeghi等[21]提出的基于池的遗传算法(Pool-GA)框架。它淡化了“代”的概念。如图3(a)所示，该框架设计了一个公用的结构池，并利用灵活的并行计算，同时运行多个遗传算法优化，并将得到的子代结构实时共享在池内，实现了更高的运算效率。如图3(b)所示，基于池的遗传算法比基于代的遗传算法能更充分地利用多核处理器资源，在相同时间内能处理更多的结构。该框架后来被进一步发展成了伯明翰并行遗传算法(Birmingham parallel genetic algorithm)，并被应用于不同大小及不同计量比的Ir团簇[44]、Au-Pd 纳米合金[45]、Ru-Pt 团簇[46]、MgO(100)表面吸附的Au-Ir[3]以及Au-Pd团簇[47]的全局优化。

2003年时，Habershon 等[48]提出了用于全局结构优化的多种群遗传算法框架，并用于复杂体系的结构优化。种群即代表一个独立运行的遗传算法优化。与标准框架相比，多种群框架除了并行执行多个优化任务，同时也需要考虑如何在种群间交换结构。常用的交换方式为移民(migrate)，即将某个种群的结构移至其他种群。Hajinazar 等[33]将多种群遗传算法用于优化Cu-Pd-Ag 团簇，不同大小的团簇独立运行一个遗传算法。在迭代一定次数后，选择种群内适应度高的团簇结构，通过添加/删除表面原子改变团簇大小，并移民至其他并行运行的遗传算法优化中。交换到大小不同的其他种群中。这样的策略提高了优化过程中的多样性，避免过早收敛至局部极值。相似的多种群策略也被Fan 等[49]用以优化Fe 团簇和Cr 团簇的结构。此处并行运行的遗传算法不仅相互独立，而且采取不同的变异策略，大大增加了优化过程中的结构多样性。

2.2 与机器学习技术联用的遗传算法框架

图3 基于池的遗传算法框架及其性能测试[21]Fig.3 The framework of pool-GA and its performance test results

2.2.1 使用机器学习加速遗传算法 在遗传算法进行全局结构优化的过程中，所有生成的结构都需要进行局部优化[30]，以此来描述势能面。但全局结构优化往往需要对大量候选结构进行局部优化[33]，计算量巨大。对于原子数较多的复杂体系，很难使用精度较高的密度泛函方法进行，通常需要使用经验势函数。而机器学习(machine learning)作为一种非线性的拟合工具，可以被足够多的结构-能量数据训练，构建高维势能面[50]，并用作计算上较为便宜但精度较高的能量计算器[51]，加快遗传算法的收敛。Hajinazar 等[33]的工作表明，使用基于密度泛函方法级别下的计算数据，训练得到的机器学习模型，其精度比经验势函数更高。

比较常用的用以构建势能面的机器学习方法有神经网络[52]、高斯过程回归[53]、核岭回归[54]等。Chen 等[55]提出了一种没有经验参数的简化结构描述符“k-Bags”，用以将结构描述成具有置换不变性、可用以机器学习训练的编码。然后使用已有的数据集(QM7[56]、GDB-9[57]等)对使用卷积神经网络进行训练，所得到的模型的能量预测误差在1.0 kcal/mol以内。Chen 等将该模型用以遗传算法的全局优化中，对比使用密度泛函方法的遗传算法，使用机器学习模型的遗传算法无论在小分子、团簇、表面吸附模型的全局结构优化中，都显示出明显的加速。

机器学习的训练高度依赖于训练集的大小及质量。除了使用公开的数据集，也可以使用第一性原理计算一批相似结构，作为训练集。Hajinazar等[33]使用密度泛函方法，得到一批用以机器学习的训练集，使用神经网络进行训练后得到机器学习模型，并将该模型与遗传算法联用，成功获得了不同尺寸下的二元Cu-Ag 团簇、Pd-Ag 团簇以及三元Cu-Pd-Ag 团簇的基态结构。关于使用机器学习构建势能面的讨论已超出本文的范围，如有兴趣可参考文献[58]。

遗传算法亦可以实现个体结构的无偏生成[17]。对缺少数据集的体系，可以使用遗传算法生成数据，由一个不完整的小型训练集出发，训练机器学习模型，同时使用该模型加速遗传算法搜索。在遗传算法迭代的过程中，再将新生成的数据用以更新模型，逐步增加模型的精度。这样的思想在机器学习中被称为主动学习(active learning)[59]。一个典型的工作来自Jennings 等[34]用以优化纳米合金的遗传算法框架。如图4(a)所示，遗传算法生成的初始种群被用以训练机器学习模型，模型被用于高通量筛选遗传算法生成的个体结构数据，仅选部分适应度高的结构在密度泛函级别下计算能量，并用以更新机器学习模型。与标准遗传算法相比，该框架所需高精度计算的次数减少至1/50，大大加速了优化效率。Bisbo等[24]使用高斯过程回归，开发出了GOFEE的机器学习框架，用以研究Ir(111)上石墨烯的基态结构。图4(b)表明，在研究表面重构的过程中，引入主动学习框架的遗传算法，其性能要比仅基于第一性原理的遗传算法高2 个数量级。Kolsbjerg 等[60]将主动学习技术与遗传算法结合，用以对MgO 负载上的Pt13团簇进行全局优化，更快地得到了比之前报道更稳定的基态结构。

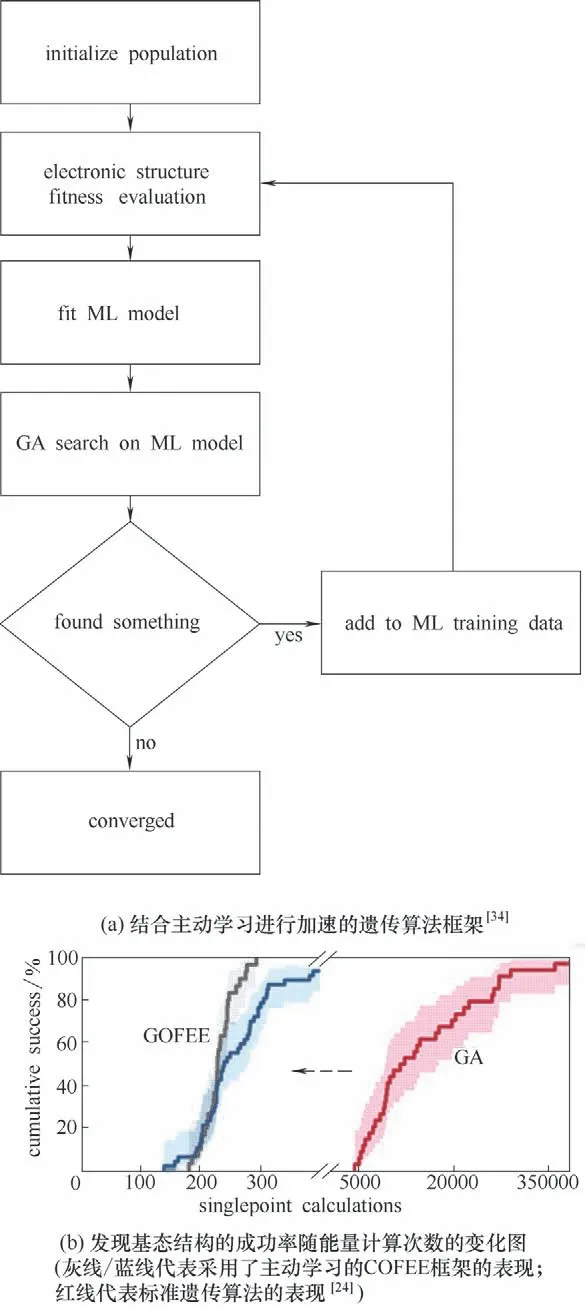
图4 结合主动学习进行加速的遗传算法框架及性能表现Fig.4 Flowchart for the active learning-accelerated genetic algorithm method and its performance test results

2.2.2 与聚类算法结合 大多数遗传算法根据适应度随机选择父代，适应度越高，则被选择的概率也越大。但单纯依赖此规则，可能造成少数适应度值较大的个体反复被选中，数次迭代后在种群中占很大的比例，导致优化收敛至局部极值。聚类算法(clustering)是把相似的对象通过静态分类的方法分成不同的组别或者更多的子集的非监督式机器学习算法。在全局结构优化中，可用于分析个体间结构上的相似性，并将相似个体聚成类簇，并做进一步 筛 选。 Jørgensen 等[42]使 用 层 次 聚 类 法(agglomerative hierarchical clustering)，在每代运行后对现有种群进行聚类分析，按照相似度分成不同类簇，并基于聚类结果，对不同个体的适应度进行调整。若某个体的结构单独形成类簇，则在生成子代时将被始终选为父代。同时，若某个体所在的类簇较大，则说明与该个体相似的结构在种群中占的比例较大，其适应度将会受到惩罚。这样，独特的结构(即便能量未必最低)将更高概率地得到保存。比起仅根据适应度随机选择父代，引入聚类算法后的遗传算法结构效率更高，能够更快找到全局最小值点。聚类算法也同样被Curtis等[35]采用，用在分子晶体结构预测程序GAtor 中，抑制相似结构的适应度。而Lyakhov等[30]在聚类后，仅将每类中最好的结构传递到下一代，抛弃其他相似结构，最大限度地保证了结构多样性。

除了用于抑制相似结构，聚类算法亦可用于结构的大数据分析，提炼基态结构的特征。Sørensen等[61]使用聚类算法对TiO2表面结构特征进行聚类，发现基态结构的键长特征，并发展为生成子代的新方法：采用梯度下降法，将父代的键长指向基态结构的键长特征进行优化，生成子代。测试结果表明，新方法能更快发现基态结构，同时证明聚类算法提炼的特征有很好的普适性，在不同大小的TiO2结构优化中均提升了优化效果。

2.2.3 与贝叶斯优化结合 作为无偏优化算法，遗传算法在势能面上的优化方向有一定的随机性。而引入贝叶斯优化(Bayesian optimization)的思想，可以指引优化的方向，加快效率。贝叶斯优化可根据势能面上的现有信息，将未知点分为“开发”(exploitation)和“探索”(exploration)：“开发”代表着势能面上未探索的陌生区域(也许存在基态结构)，“探索”则代表已知具有低能量结构的区域。何时“开发”，何时“探索”的权衡由固定的权重值控制。贝叶斯优化依赖先验知识，来推测势能面的后验分布。Jørgensen 等[62]将贝叶斯优化引入遗传算法框架中，由遗传算法生成的数据提供先验分布，探究了“开发”和“探索”的权重值与优化结果的关系，并用于C10H6O2体系的结构优化中，得到了比标准遗传算法更快的优化效率。该框架也被后续开发为全局结构优化的遗传算法工具包GOFEE[24]。

2.3 与其他优化算法结合

在一些优化问题中，将多种全局优化方法联用，取长补短，能收获更好的效果[63]。例如，遗传算法的优势在于其强大的全局搜索能力，但其局部搜索能力受限，即难以在某一限定区域内优化目标函数[64]。相反，模拟退火等算法则具有很强的集中性搜索能力，但多样化能力很弱。Zacharias 等[65]将模拟退火和遗传算法结合，用以优化硅团簇。在优化前期使用遗传算法，快速搜索解空间，而后期使用模拟退火，在局部进行集中搜索。结果表明，两者结合的混合方法比单一算法更高效地收敛。Liu 等[4]在优化不同大小及化学计量比的硫醇盐保护的金团簇时，使用由盆地跳跃得到的局域极小值作为初始个体，再使用遗传算法进行优化，亦避免了使用单一优化方法容易陷入局域极小值的缺点。Cai 等[66]将模拟退火算法和遗传算法相结合，开发出了团簇全局结构优化的程序包PFAEA，成功优化了包含了数百个原子Lennard-Jones 团簇，证明了混合算法在解决原子数较多的复杂体系的潜力。

3 遗传算法在催化领域的应用实例

3.1 金属团簇催化剂的结构优化

金属团簇作为化工生产中最重要的催化剂之一，其催化性能与结构有紧密的关系。只有找到了团簇的基态结构，才能在此基础上研究其电子催化活性等各种性质。但团簇的结构多变，可呈现链状、管状、平面、核壳等多种结构形式，使其具有更加复杂的势能面。并且，改变团簇中任一原子的位置，都可能造成催化性质的巨大差异。而由于团簇结构的复杂性，实验上很难系统地观测团簇的基态结构，需要结合理论计算来确定基态结构。并且随着原子数增加，团簇可能的构型数目急剧增加，通过穷举找到基态结构是极其困难的。

由于其在各领域中的广泛应用和相应优化问题的困难性，金属团簇的全局结构优化问题一直是遗传算法的应用热点。早在20世纪末，遗传算法就被成功用于Si4[13]和C60[14]团簇的结构优化中，并可能实现比其他技术更高的优化效率[67]。针对团簇结构优化问题，一系列成熟的遗传算法框架也被提出和应用，例如Alexandrova 等[68]开发的嵌入式梯度遗传算法(gradient embedded genetic algorithm)、Dieterich等[69]开发的OGOLEM 框架、Davis 等[3]开发的伯明翰并行遗传算法以及Vargas 等[70]开发的墨西哥增强遗传算法(Mexican enhanced genetic algorithm)等。

3.1.1 单金属团簇 Au 团簇的结构可以在分子水平进行调控，因此被认为是团簇研究中良好的模型系统[71]。对Au 团簇体系进行全局结构优化研究，有助于理解团簇的结构与性能之间的关系。如图5(a)所示，Assadollahzadeh 等[72]通过遗传算法，对中性Au2-20团簇的基态结构进行了研究，计算结果表明中性Aun团簇由二维向三维的转变发生在Au13与Au15之间，且Au20团簇呈现高对称四面体形状。Au20团簇的结构形貌图也在近年通过簇束沉积和低温扫描隧道显微镜等表征手段而获得[23]，验证了遗传算法的可靠性。Li 等[73]对Au38-55团簇的全局优化结果则表明，随着尺寸的增加，Au 团簇的基态结构将从紧密堆积结构转变为核壳结构，并由于短程作用力的存在，能量最低的基态结构倾向于无序结构。

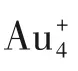
3.1.2 合金团簇 由于可以充分利用多种金属间的协同效应，合金团簇通过调控，可以实现多功能性和高反应性，在催化领域具有较大的应用潜力[77]。Xie 等[78]报道了Pd 掺杂后的Au25团簇，对苯甲醇的催化转化率从22%显着提高到74%。Liu 等[79]报道了Ag 原子的引入可以缩小Au23-xAgx团簇的禁带宽度并增强反应稳定性，提高光催化性能。而合金团簇的基态结构是研究其催化活性、设计合金团簇催化剂的重要基础。由于存在等位(homotopic)同分异构体，即原子成分和几何结构相同，但原子排布不同的结构，合金团簇的结构优化难度更高，需要使用全局优化等方法进行解决。

Heiles 等[80]使用伯明翰簇并行遗传算法，研究了中性八聚体Au-Ag 团簇的计量比与结构的关系，并预测基态结构由二维向三维的转变发生在Au6Ag2和Au5Ag3之间。Demiroglu 等[46]对Pt-Ru 团簇的全局结构优化则表明，在基态结构下，铂原子更喜欢外围位置，而钌原子则倾向处于中心位点，并生成更强的Ru-Ru 键。而对PdnIrN-n(N=8～10)团簇的全局结构优化则表明，当Ir含量较多时，团簇为立方体结构，而当Pd量较多时，则为紧密堆积结构，且偏析效应严重[81]。另外，对于常见的合金催化剂，如Au-Pd团簇[45]、Au-Cu 团簇[82]等，亦有全局结构优化的工作报道。

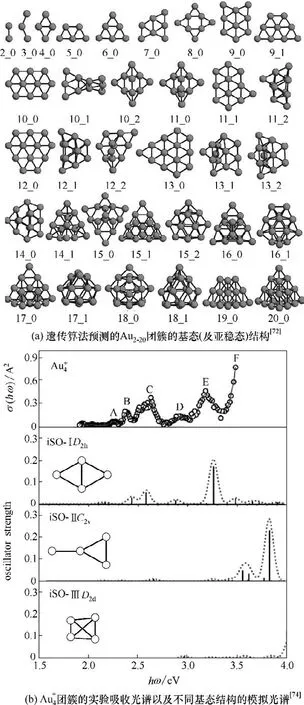
图5 不同尺寸和电荷下的Au团簇的基态结构Fig.5 The global minimum structure of Au cluster with different size

3.1.3 团簇生长过程 对催化剂材料生长过程的精确理解，对实现催化剂的按需设计具有重要意义。实验上，团簇催化剂的表面成长过程可通过电喷雾电离-质谱等方法[83]鉴定，但仅从实验出发，缺少在分子尺度上，对团簇生长机理的尺寸效应的理解。而从理论计算上，结合遗传算法，可通过对不同尺寸的团簇进行全局优化，构建其成核、成长过程，帮助理解团簇的结构随尺寸变化的过程。Liu 等[4]将遗传算法与盆地跳跃法联用，计算了不同大小及计量比的硫醇配体保护的Au 团簇的基态结构，成功分析了Au 团簇的逐步成核与生长规律，如图6(a)所示。Hussein 等[84]使用伯明翰遗传算法，阐明了中性Pb16-18为类球形的笼状结构，其生长过程呈现出fcc 的特征。而对Ni-Al 合金的全局结构优化则表明[85]，往Ni28Al10团簇添加1 个Ni 原子生成Ni29Al10团簇的过程，基态结构将从截角八面体变为二十面体。而继续添加原子，基态结构仍然维持二十面体构型，直到形成双层二十面体的Ni41Al14结构。

除了全局最小值结构，遗传算法在搜索过程中产生的亚稳态结构亦可以用于构建反应路径，揭示反应中团簇催化剂结构的动态演化过程。如图6(b)所示，Liu等[4]在研究Au团簇的逐步成核与生长规律时，同时选择了一批与基态结构相似的亚稳态结构，作为Au 团簇生长过程中的中间体，更动态地了解团簇成核及生长过程。

3.2 负载型催化剂的结构优化

由于产物易分离，耐高温等特性，负载型催化剂有着较好的催化性能[86]。对于负载型催化剂而言，载体的影响时常是不可忽视的。载体能够影响催化剂在其表面的分散情况、粒径大小等，导致催化剂的结构与气相中有很大不同[87]。通过调变载体与催化剂之间的相互作用，亦可以调控催化性能。对负载型催化剂进行全局结构优化，有助于了解载体对催化剂结构影响，理解表面催化过程，帮助理性设计新型、高效催化剂[3]。针对负载型金属催化剂的全局结构优化，常用使用周期性平板模型，相关的遗传算法框架有Vilhelmsen 等[16]开发的内置于原子模拟环境（atomic simulation environment，ASE)[88]的遗传算法模块以及Sierka[12]开发的混合从头算遗传算法(hybrid ab initio genetic algorithm)等。

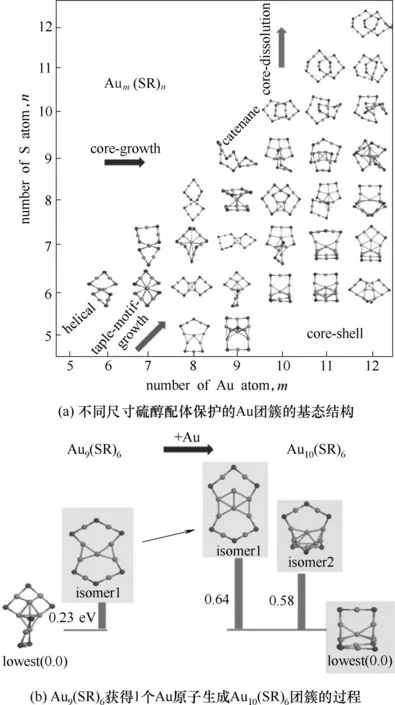
图6 不同尺寸硫醇配体保护的Au团簇及其成核、成长过程[4]Fig.6 Schematic illustrations of the size-evolution of Aum(SR)n clusters

3.2.1 催化剂结构 Zhang等[86]使用遗传算法，分别对气相及不同载体负载的Au8团簇进行了全局结构优化，结果显示，气相中Au8团簇倾向于片状结构，而在氧化石墨烯上，则锚定在环氧位点上，生成三维结构。Au8团簇吸附在金红石TiO2(110)时形成了牢固的Ti-Au 键，基态结构同样也三维结构。Davis等[3]使用伯明翰并行遗传算法，分别对气相下和MgO(100)吸附时的Au-Ir 团簇进行全局结构优化。如图7(a)、(b)所示，MgO(100)负载的Au-Ir 团簇倾向于最大程度增加Ir-O 键的数量，并形成低自旋结构，与气相下的结构有着显著差异。Vilhelmsen等[89]则研究了金属有机框架(metal-organic framework,MOF)吸附的Au8、Pd8和Au4Pd4团簇的基态结构，结果表明Pd 比Au 对MOF 的结合力更强，Au 和Pd 并不倾向于形成合金团簇。同时，MOF 上的金属位点对金属催化剂的吸附未有明显作用。该结果可以帮助了解和预测MOF 上的局部环境如何影响对催化剂的结构。

在使用遗传算法优化负载型催化剂的结构时，亚稳态结构同样也可以用于构建结构的演化过程。但在使用亚稳态结构作为中间体，分析反应路径时，一个无法避免的问题是如何对遗传算法产生的大量亚稳态结构进行匹配。对亚稳态结构匹配不合理时，所构建的反应路径也将不合理。Zhai等[9]使用图论中的匈牙利算法，利用两个结构间的相似度等信息，对大量亚稳态进行两两配对，并使用微动弹性带(nudged elastic band,NEB)方法搜寻它们间的过渡态结构，构建了Pt7团簇在α-Al2O3表面上的各个结构形态间相对能量关系以及变化过程，结果如图8所示。另外，值得一提的是，遗传算法也被用于寻找复杂的过渡态结构(势能面反应路径上的极大值点)。Yang 等[17]使用遗传算法，搜索含非共价相互作用的催化反应体系的过渡态，并成功应用于不对称斯特雷克反应和不对称醇解反应的过渡态搜索中。

3.2.2 反应物对结构的影响 亚纳米尺度的金属催化剂(包括单个原子和团簇)由于其结构的灵活性，在与反应物相互作用时会呈现动态的结构演化，导致真实的活性结构与其初期吸附结构有所差异，从而难以确定催化活性结构。He 等[90]通过环境电子透射显微镜，观察到在反应气氛下，CeO2(111)上单层Au 团簇会从面心立方密堆积转变为无定形状态。通过理论计算，确定催化剂在反应物参与下的真实活性结构，对从分子水平了解反应机理和设计更有效的催化剂至关重要。

Sierka 等[87]使用遗传算法，研究了Mo(112)表面吸附的SiO2基态结构随硅覆盖率以及氧气压力的变化，并绘制相图。计算结果成功预测了在高氧气压力下形成的未被报道的二维SiO2薄膜结构：除了形成角共享[SiO4]四面体外，部分氧原子还直接吸附在Mo (112)表面上。该结构亦被红外反射吸收光谱(IRAS)和X 射线光电子能谱(XPS)所确认。Sun 等[91]使用遗传算法，研究了α-Al2O3(0001)和γ-Al2O3(100)表面上不同氢原子吸附下形成的Pt8团簇的基态结构。如图9 所示，不同的载体并不影响氢原子的最佳吸附数量，但对团簇的结构影响很大。在较少氢原子吸附时，α-Al2O3(0001)表面的Pt8Hx团簇呈现拟二层状，而γ-Al2O3(100)的则为单层；而在较多氢原子吸附时，α-Al2O3(0001)表面的Pt8Hx团簇呈现完全平整状，而γ-Al2O3(100)的则为三维球状结构。

Vilhelmsen 等[92]使用遗传算法研究了MgO(100)负载的Au8团簇吸附O2的过程。在确定O2能量最低的吸附位点后，通过遗传算法对Au8团簇的结构进行优化，揭示了O2吸附后Au8团簇的结构变化过程，结果如图10 所示。Fang 等[6]使用遗传算法，研究了Au(100)表面的CO 氧化过程，结果表明氧化过程中，Au(100)表面将重构为六角形相，并生成O-Au-O 物种。由于O-Au-O物种能直接与吸附的CO反应，重构后的Au(100)表面对CO 有更好的催化性能。而Fang 等[6]同样将遗传算法优化过程中产生的亚稳态结构作为中间体，用以构建重构过程的势能面，阐明了表面重构过程的反应路径。

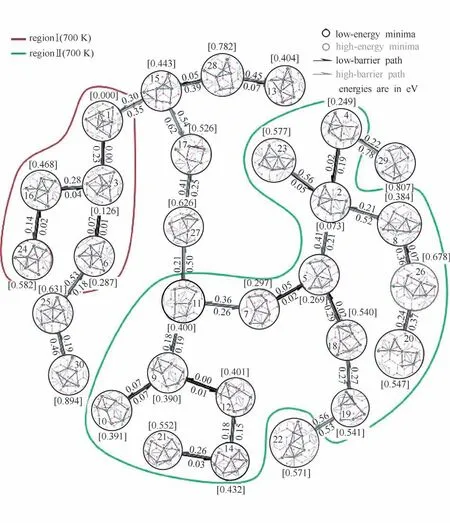
图8 Pt7团簇在α-Al2O3表面上的演化过程[9]Fig.8 The evolutionary process of Pt7 cluster on α-Al2O3 surface[9]

图9 α-Al2O3(0001)吸附的Pt8H4团簇(a)，γ-Al2O3(100)吸附的Pt8H5团簇(b)，α-Al2O3(0001)吸附的Pt8H24团簇(c)和γ-Al2O3(100)吸附的Pt8H24团簇(d)的基态结构[91]Fig.9 Global minimum structure of Pt8H4 on α-Al2O3(0001)(a),Pt8H5 on γ-Al2O3(100)(b),Pt8H24 on α-Al2O3(0001)(c),and Pt8H24 on γ-Al2O3(100)(d)[91]

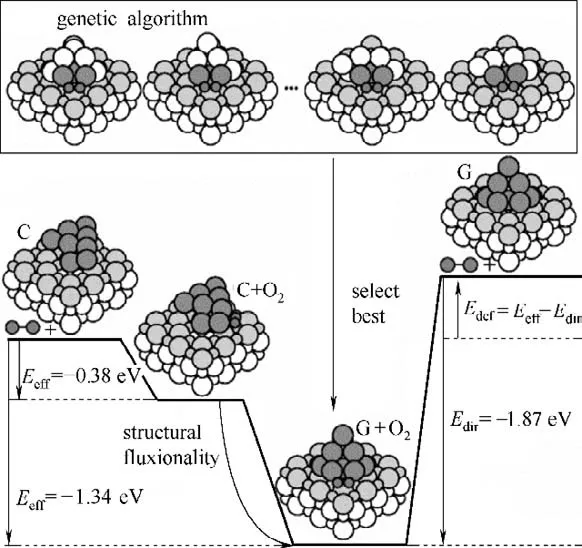
图10 O2在MgO(100)负载的Au12团簇的吸附过程[92]Fig.10 The adsorption process of O2 on the MgO(100)-supported Au12clusters[92]

4 结论与展望

遗传算法作为一种无偏优化算法，在优化中不依赖于已有的结构，具有很强的全局搜索能力。将遗传算法应用于催化体系中各种复杂的优化问题中，为催化研究提供了新的视角。然而，该领域的研究仍旧存在一些亟待解决的问题：(1)现有遗传算法难以用于原子数较多的复杂体系中，势能面的复杂程度随着体系原子数目的增加而增加，极小值点个数也以指数形式增长，而现有优化策略在处理复杂体系势能面时，面临着取样效率不足的缺陷，同时，越复杂的体系，优化过程往往需要对大量候选结构进行能量评估，对计算资源的要求也随之增加；(2)现有遗传算法仍具有很大的随机性，由于缺少对基态结构的普遍性先验认知，无法对遗传算法的搜索方向进行引导，只能依赖结构能量作为唯一标准，导致遗传算法效率较低，需要进行多次迭代、计算大量的候选结构才能发现基态结构。

未来遗传算法将继续向并行化(充分利用计算资源)、智能化(使用机器学习方法降低不必要的高精度计算次数)、通用化(能处理各类复杂的体系)的方向发展，加快优化速度，以较少的计算代价获得基态结构。同时，亦有必要继续加深对基态结构的理解，以实现对优势构象的增强采样，减少在势能面的盲目探索，进一步提高遗传算法的搜索效率。相信遗传算法在面对催化体系中各种复杂的结构优化问题中能发挥更重要的作用。