一类函数型复微分方程的整函数解

卫玉明，刘 凯，高迎春

(南昌大学理学院数学系，江西 南昌 330031)

1 引言与主要结果

本文中，我们假设读者熟悉Nevanlinna理论[1-2]的基本概念和符号，且f(z)为复平面上的亚纯函数。对于非线性函数方程而言，利用Nevanlinna理论可以得到其亚纯函数解的存在性、增长性和零点极点等方面的性质，然而求其所有的亚纯函数解的形式往往是很困难的事情。在文献Yang和Li[3]，Heittokangas,Korhonen和Laine[4]中，作者通过观察三角公式sin3z=3sinz-4sin3z,研究了一类重要的的非线性微分方程

4f(z)3+3f″(z)=-sin3z

(1.1)

的亚纯函数解的性质，并得到了下列结果:

定理A[3]方程(1.1)只有3个亚纯函数解且都是整函数,分别是

f(z)n+P(f)=p1eα1z+p2eα2z

(1.2)

这里的P(f)是f(z)的微分多项式，p1,p2,α1,α2是非零常数,n(≥3)是正整数。这方面的结果可见文[5-6]，后来大家也研究了P(f)是差分或者微分差分或者q-差分形式的函数方程的亚纯函数解[7]。

基于常用的三角函数公式sin(z1+z2)=sinz1cosz2+cosz1sinz2。如果sinz被函数f(z)代替，cosz被f′(z)代替，便得到了下列的微分方程:

f(z1+z2)=f(z1)f′(z2)+f(z2)f′(z1)

(1.3)

Zhang和Yi[8，定理1.2]得到了下列结果:

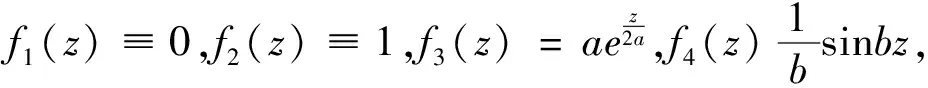
注1在证明定理B的过程中，Zhang和Yi利用了正规族的一些理论，特别是Zalcman引理起到了重要作用，得到了方程(1.3)的亚纯函数解的增长级为不超过1的结论。事实上此结论可以利用引理2.2得到。

本文我们基于另外一个重要的三角函数公式，cos(z1+z2)=cosz1cosz2-sinz1sinz2,类似的，我们用f(z)替换cosz,用-f′(z)替换sinz,得到了下述微分方程:

f(z1+z2)=f(z1)f(z2)-f′(z1)f′(z2)

(1.4)

显然f(z)=cosz为上述方程的一个亚纯函数解，我们首先给出关于方程(1.4)亚纯函数增长性和存在性结果。

定理1.1方程(1.4)不存在非整函数的亚纯函数解，方程(1.4)的整函数解的增长级ρ(f)≤1。

下面的定理刻画了方程(1.4)的整函数解的形式。

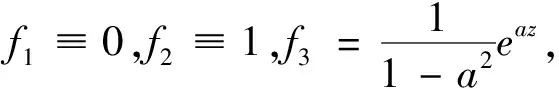
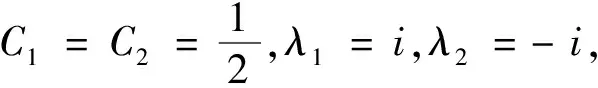
2 引理

引理2.1[9]对于任意的亚纯函数f和任意非零常数q，下面的等式成立

T(r,f(qz))=T(|q|r,f)+O(1).

引理2.2[10]令Φ:(1,+∞)→(0,+∞)是一个在复平面上的单调递增的函数，f是非常数亚纯函数，如果对于一些实常数α∈(0,1),存在实常数K1>0和K2≥1使得

T(r,f)≤K1Φ(αr)+K2T(αr,f)+S(αr,f),

则f的增长级满足

注3通过文献[10]中涉及的关于引理2.2的证明过程，上述引理对于去掉Φ(r)的有关项后，结论也是成立的。

3 定理的证明

定理1.1的证明假设方程(1.4)存在有极点的亚纯函数解f(z)，那么当z1=z2=z时，方程(1.4)可以转化为

f(2z)=f(z)2-f′(z)2

(3.1)

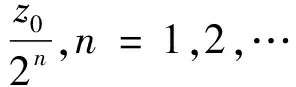
下面我们证明所有的整函数的增长级满足ρ(f)≤1。由引理2.1可以得到

T(r,f(2z))=T(2r,f(z))+O(1)

(3.2)

因为f(z)为整函数，利用对数导数引理可以得到

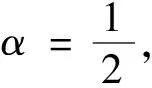
定理1.2的证明首先假设f(z)是次数为n(n≥1)的多项式。对于方程(3.1)，我们得到f(2z)的次数为n，f(z)2-f′(z)2的次数为2n，矛盾。所以f(z)必为常数。令f(z)≡c,c是一个常数,则有c=c2,则有c=0或c=1。因此f1≡0,f2≡1。

下面假设f(z)是超越整函数。首先令z1=0,z2=z,我们得到

f(z)=f(0)f(z)-f′(0)f′(z)

(3.3)

现在我们分下列两种情况讨论。

情形1当f′(0)≠0.我们得到

令a是非零常数，则有

f(z)=ceaz

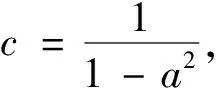
情形2当f′(0)=0,通过方程(3.3)得到f(0)=1。在方程(1.4)中，对z2求导得到

f′(z1+z2)=f(z1)f′(z2)-f′(z1)f″(z2)

(3.4)

对于(3.4)式，分别对z1,z2求导，得到

(3.5)

对于(3.5)式，令z1=z2=z,得

f′(z)(f′(z)+f‴(z))=f″(z)(f(z)+f″(z))

(3.6)

显然f′(z)和f″(z)不可能恒等于0。当f(z)+f″(z)≡0时。得

f(z)=Aeiz+Be-iz,

这里的A,B是非零常数。将f(z)代入(1.4)得

A(1-A-A)ei(z1+z2)+B(1-B-B)e-i(z1+z2)=0,

所以

因此A=B=1/2,因此我们有f(z)=cosz。

当f(z)+f″(z)不恒等于零时。由(3.6)得到

对上式两边积分得

f(z)+f″(z)=Cf′(z),