基于粗糙集自适应粒度的MR脑肿瘤图像分割

姚传文,黄道斌,叶明全

(1.皖南医学院医学信息学院,安徽 芜湖 241002; 2.皖南医学院健康大数据挖掘与应用研究中心,安徽 芜湖 241002)

0 引 言

磁共振(MR)脑肿瘤图像分割是利用计算机技术将肿瘤区和正常组织区进行分割标注，对于脑肿瘤辅助诊断具有重要作用[1-2]。但是，由于脑组织和脑肿瘤的复杂性，以及MR图像模糊、灰度不均匀等问题[3]，使得脑肿瘤图像分割成为医学图像处理和智能医学领域研究的热点和难点[4-8]。通常，图像分割依赖于对图像目标、背景和边缘的识别和分类，图像边缘具有一定的不确定性，导致图像目标分割精度直接依赖于边缘阈值的选取。

近年来，一些研究者将粗糙集应用于图像分割，并取得系列研究成果[9-13]。Pal等[14]于2005年发表论文，认为图像边缘具有不确定性和模糊性的问题，可通过目标或背景的粗糙集上下近似描述。然而，粗糙集分割方法需要人工指定粒度大小，限制了其在实际中应用。2014年，吴涛[15]提出图像阈值化的自适应粗糙熵方法，利用局部灰度标准差选取最优分割粒度，确定图像分割的阈值。

本文利用粗糙集自适应粒度方法选取最优分割粒度，并用粗糙集模拟目标和背景区域的上下近似，通过优化上下近似的粗糙度，获得MR脑肿瘤图像分割的最佳阈值。实验结果表明，该方法优于传统粗糙集分割法，且具有一定实用性和灵活性。

1 图像分割粗糙集理论

1.1 粗糙集理论

粗糙集理论是1982年被波兰科学家Pawlak[16]提出。利用数据间存在不确定性关系，通过集合运算的方式定义上近似和下近似，得到数据相似性和粗糙性的关系。假设数据为S=(U,A,V,f)，X⊆U，R⊆A，其中论域U为非空有限对象集，A为描述对象的非空有限属性集，V为所有属性值集，f为U×A→V上的一个信息函数，等价类数值属性集R为Ri=[x]R，则对象X通过粗糙集的等价类关系定义上近似与下近似：

R*(X)=∪{Ri|Ri∈U/R∧Ri⊆X}

(1)

R*(X)=∪{Ri|Ri∈U/R∧Ri∩X≠∅}

(2)

根据数值属性的数据，上近似和下近似的关系还可分别定义为：

R*(X)=∪{[x]R|[x]R⊆X}

(3)

R*(X)=∪{[x]R|[x]R∩X≠∅}

(4)

上近似、下近似和边界域3者之间的关系，如图1所示。

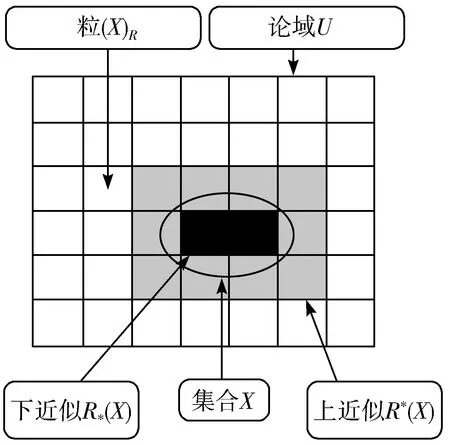
图1 粗糙集近似关系

1.2 图像分割粗糙集定义

图像中所有像素构成的像素集称为论域U。如果将该图像划分为k个粒度大小为m×n且互不相交的像素子集，则每个子集可被看成是等价划分后的粒度G。显然，图像中目标可以用粗糙集理论来描述，即目标上下近似可以分别表示目标内含有的最大粒簇和目标外含有的最小粒簇。因此，通过粒度大小变化调节，对边界域的近似刻画能有效逼近目标。

MR脑肿瘤图像处理过程中，可将图像分割成感兴趣的区域即目标O和背景B这2个部分。设图像灰度值在{0,1,…,L}之间，图像所有像素构成论域U，U上的映射g：U→{0,1,…,L}为任意像素P处的灰度值用g(P)表示。为便于描述，假定分割边缘区域阈值为T，目标灰度值大于背景灰度值，则将图像划分为灰度值在{0,1,…,T}范围的背景BT和灰度值在{T+1,T+2,…,L}范围的目标OT。根据粗糙集理论可得到目标和背景的上、下近似集分别为OT、OT和BT、BT:

(5)

(6)

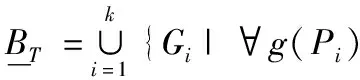
(7)

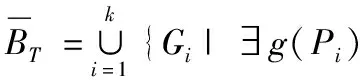
(8)

根据式(5)～式(8)中上、下近似集中图像目标和背景的关系，可得到对应目标和背景的边界域：

(9)

(10)

1.3 自适应粗糙粒度准则

基于粗糙集自适应粒度的MR脑肿瘤图像分割，关键是根据已知上、下近似集得到图像目标和背景，如何确定分割边界区域的阈值。同时，在给定条件下选取不同m×n的粒度G，对边界域阈值的确定会产生什么影响。

假设图像I给定的粒度为Gi，Gi大小为m×n，图像像素变化程度可通过图像粒度的局部灰度标准差(Local Gray Standard Deviation，LGSD)来计算，即：

(11)

(12)

(13)

显然，当图像的LGSD达到最大值时，可将此时粒度大小作为粗糙集图像分割算法的最优粒度。

1.4 粗糙集自适应粒度分割方法

根据粗糙集不确定性的定义，图像目标和背景的粗糙度分别为：

(14)

(15)

根据目标和背景的粗糙度，可得到图像粗糙熵：

(16)

根据式(16)，粗糙度越小，则粗糙熵越大[11]。当粗糙熵达到最大时，则可获得最优的图像分割阈值T*，T*可定义为：

T*=arg max RET

(17)

本文方法流程图如图2所示。

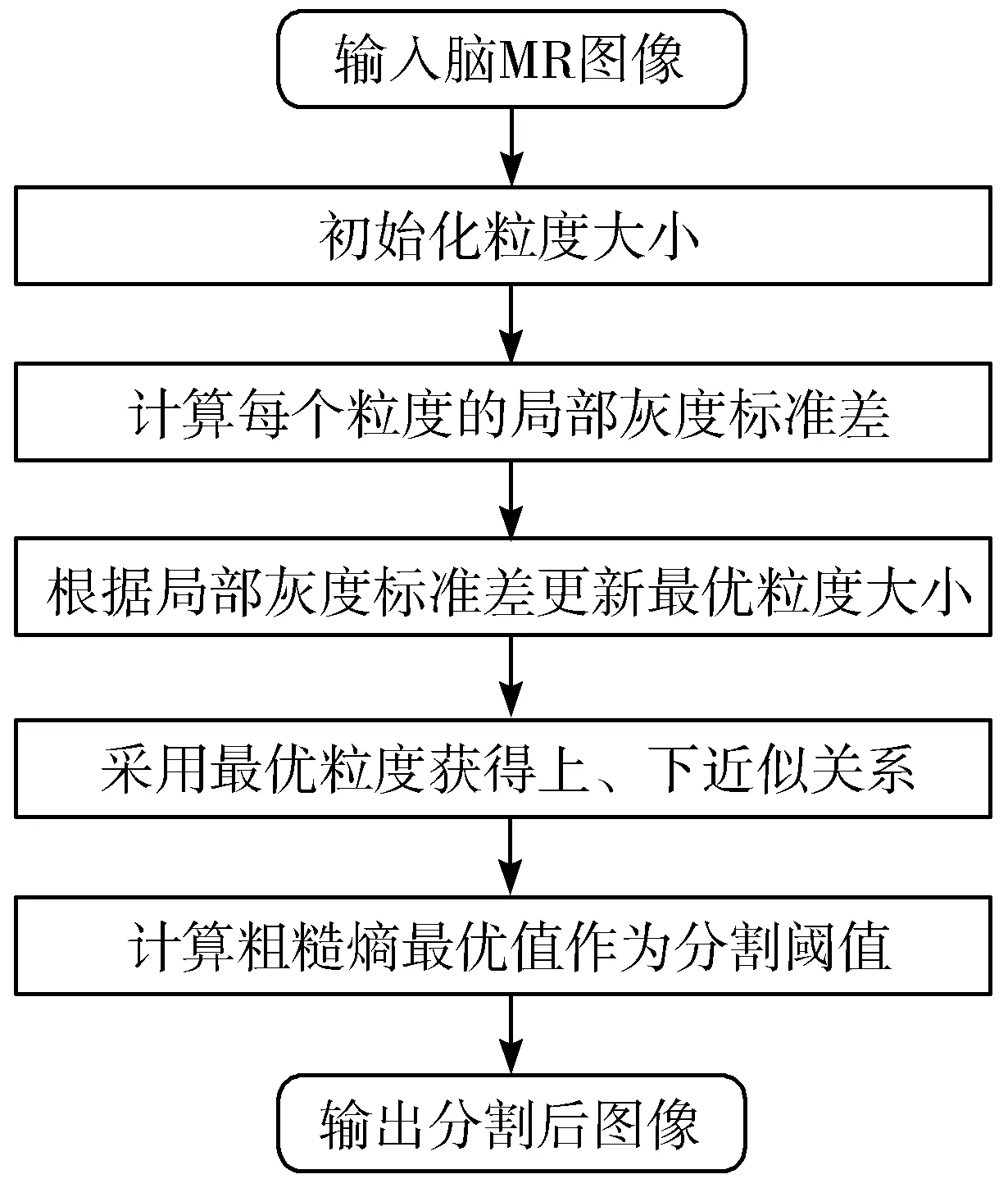
图2 粗糙集自适应粒度方法流程图

2 MR脑肿瘤图像分割实验

为验证本文方法的有效性和实用性，实验选用公开的BRATS2017数据库[17]中MR脑肿瘤图像作为测试数据。实验在Matlab2012a环境下Inter G3250 CPU、4 GB RAM、Windows7中进行，且对某位患者MR脑肿瘤图像序列中第80个～第90个层面进行图像分割。以第85幅图像为例，图3所示为传统粗糙集人工指定40×40粒度大小和粗糙集自适应粒度方法自动选定35×35粒度大小的分割结果。显然，粗糙集自适应粒度方法对肿瘤分割有明显改善。

(a)MR脑肿瘤图像 (b)传统粗糙集分割方法 (c)粗糙集自适应粒度分割方法

通过经验丰富的影像科医生手动标注和勾画病灶区可得到“金标准”图像，能够指导学者对医学图像分割方法进行完善。本文采用Dice系数(Dice Coifficient，DC)和Jaccard系数(Jaccard Index, JI)2个评价标准对分割结果进行比较，DC和JI分别定义为：

(18)

(19)

其中，X、Y分别表示分割算法提取的目标和“金标准”目标。DC∈[0,1]，其中DC=0时分割结果和“金标准”完全不一致；DC=1时分割结果和“金标准”完全一致。因此，DC越接近1，表明分割质量越好。JI∈[0,1]，其中JI=1表示分割结果与“金标准”完全一致。因此，JI越接近1，表示分割精度越高。

表1为传统粗糙集人工指定不同粒度大小情况下针对第80幅图像分割时Dice系数和Jaccard系数结果。表2为传统粗糙集人工指定20×20和40×40粒度大小和粗糙集自适应粒度方法自动选定35×35粒度大小情况下针对第80幅、第85幅、第90幅图像分割时Dice系数和Jaccard系数结果。

表3为传统粗糙集人工指定20×20、40×40粒度大小和粗糙集自适应粒度方法自动选定粒度大小情况下针对第80～第90个层面的统计学表示。

从表1～表3可以看出，在不同大小粒度的影响下，指定粒度大小对分割性能影响比较大，自适应粒度方法对粒度的选取具有较好的稳定性，充分反映出本文方法具有更优的分割性能。

表1 不同粒度下分割结果对比(以第80幅图像为例)

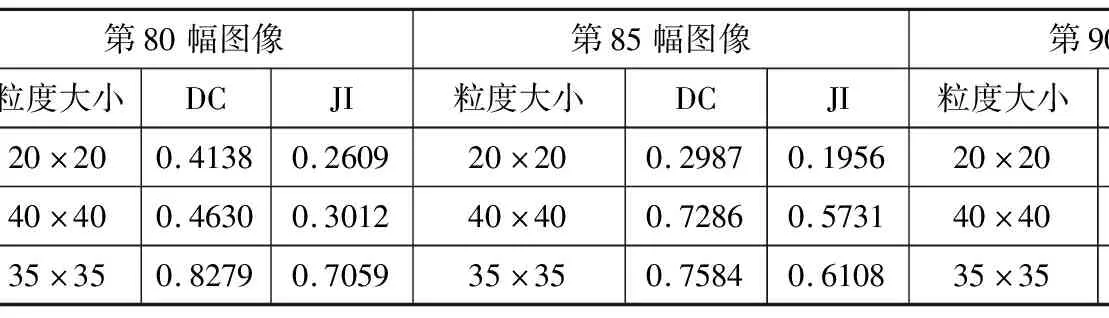
表2 指定粒度与自适应粒度分割结果对比

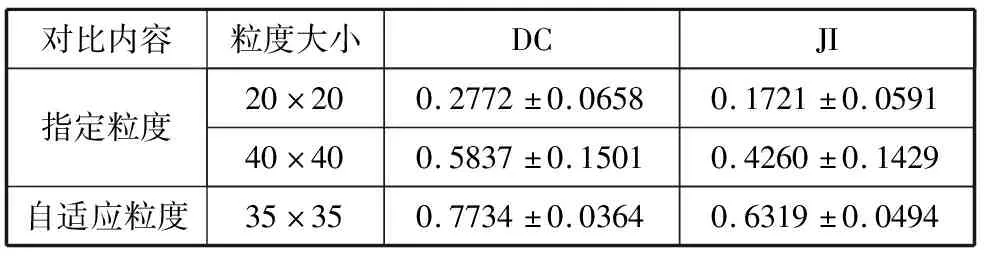
表3 分割结果统计对比

3 结束语

基于粗糙集自适应粒度的MR脑肿瘤图像分割方法充分利用粒度大小对粗糙集影响的差异性，通过最大粗糙熵自动获取最优粒度，提高脑肿瘤分割的准确性，且具有一定实用性和灵活性。

在现代医学中，医学影像技术己成为医生诊断疾病的重要依据，为临床医学提供更加可靠的信息是未来医学影像诊断技术发展的趋势。因此，下一步工作是提高肿瘤区域分割精度和鲁棒性的研究，结合聚类方法提供更准确的分割信息[18-23]。