对流层散射信道中5G-NR LDPC码性能
王博远,张 涛,王 伟
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引 言
对流层散射通信是利用对流层中的不均匀介质对电磁波产生的前向散射进行通信[1]。由于散射信道中,信号的衰落十分明显,需要采用高效的编码方式来抑制衰落。低密度奇偶校验码(Low Density Parity Code, LDPC)是一种线性分组码,由于其校验矩阵的稀疏性而得名。大容量传输是目前散射通信的发展方向[2],而LDPC码可以实现高速并行低延迟译码,是一种很好的编码选择。目前在5G NR标准中采用的LDPC码(Fifth Generation New Radio LDPC,5G-NR LDPC)支持多种码率(1/5~8/9)以及多种码长(信息长度40 bit~8448 bit),使其能够很好地支持速率自适应和大容量传输应用[3-5]。5G-NR LDPC是一种复杂度低、易于硬件实现、抗干扰能力强和编码增益较大的编码选择,这些特点使LDPC码适合作为散射通信中的编码方案。本文主要利用分集接收技术,提出一种改进的分层归一化最小和译码算法(Modified Layered-Normalized Minimum Sum Decoding Algorithm,ML-NMSA),使用分层译码的方式来减少迭代次数,降低复杂度。然后在译码算法中引入增益因子λ,矫正被缩放因子α抑制过度的节点,来提高整个算法的译码性能。最后找出不同码率下最佳缩放因子α,以适应散射信道。
1 散射信道模型
在散射信道中,一般的接收信号大部分属于“典型散射信号”,接收信号幅度以瑞利分布为主,偶有莱斯分布和大气波导,相位服从均匀分布[6-7]。假设发射信号表示为:
s(t)=Acos(2πf(t)+θ(t))
(1)
本文选择接收信号幅度服从瑞利衰落:
(2)
那么接收端的信号表示为:
r(t)=c(t,z)·Acos(2πf(t)+θ(t))+n(t)
(3)
其中,θ(t)服从0~2π均匀分布,n(t)表示噪声。
散射信号在小尺度衰落方面主要表现为快衰落特性,它具有空间选择性,相距几十个波长的不同接收点衰落特性不相关,同时具有频率选择性,相差几兆或十几兆赫兹的2个工作频率统计独立[8]。故需要采用多重分集的方式对发射信号进行发送,在接收端进行分集接收合并。
接收合并的大部分方式属于线性合并,它是不同衰落支路的加权和[9-10],如图1所示。合并后的信号是原始发送的信号乘以一个随机的复系数。合并输出的信噪比,也是一个随机变量,其概率分布取决于分集个数及合并方式,本文采用8重和16重分集,合并方式采用最大比合并。在最大比合并中,输出是各个支路的加权和。
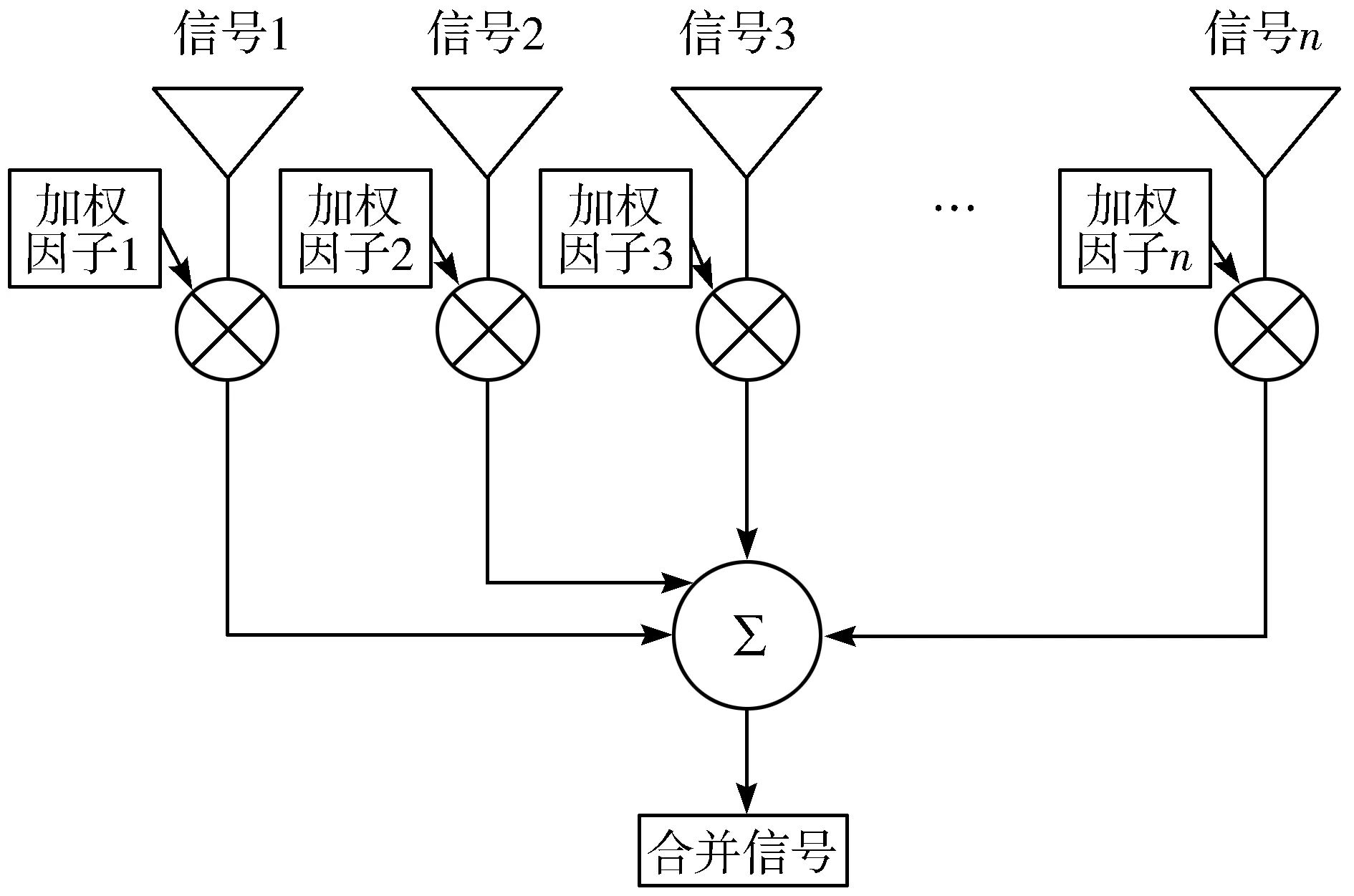
图1 分集合并原理图
2 5G-NR LDPC码的基本介绍
5G-NR LDPC码是一种准循环LDPC码[11-13],具有QC-LDPC码的全部优良性能,并在其上进行改进。5G-NR LDPC校验矩阵的构造通过基矩阵来完成。图2是5G中的基矩阵bgn2,矩阵中的每一个元素都对应着一个Z×Z的单位矩阵或者0矩阵。灰色部分代表非负元素hb(i,j),白色部分代表-1。

图2 基矩阵bgn2示意图
5G中的基矩阵需要根据扩展因子[14-15]对选定的基本矩阵Hb进行更新,计算公式如式(4),其中hb(i,j)为Hb中的元素。
(4)
为了保证5G-NR LDPC码任意码长的实现,基矩阵的前2列作为打孔比特[16]。表1给出了5G和802.16e标准下的LDPC码在基矩阵信息位和码率、码长方面的不同[17]。
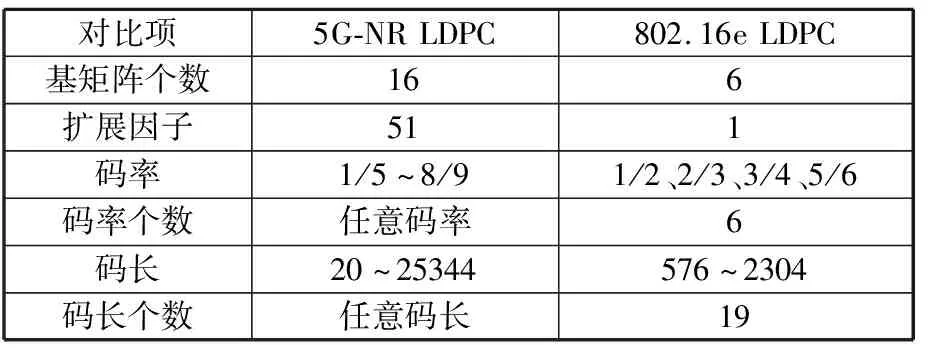
表1 5G与802.16e标准下的LDPC码对比
从表1中可以看出,5G-NR LDPC在码率和码长的选取上有着更明显的优势,均为任意码长,范围比802.16e更广,在码率和码长上有更多的选择。
3 5G-NR LDPC编译码
3.1 5G-NR LDPC码的编码
在进行基矩阵的更新扩展后即可进行编码,将源信息序列输入到编码器中进行编码得到编码序列,并将编码后的结果表示为c=[SP]。其中S=(s1,s2,…,sk)表示长度为k的信息比特序列,P=(p1,p2,…,pm)表示长度为m的校验比特序列,它们之间服从n=m+k,n是码字长度,基矩阵Hb是一个mb×nb的矩阵,核心矩阵是一个mc×nc的矩阵[18-19]。
对信息比特序列S按照每Z个比特分为一组,总共可以分为kb=nb-mb组,将分组后的比特序列记为s=[s(0),s(1),…,s(kb-1)];同理,对校验比特序列P进行同样的操作,总共可分为mb组,记为p=[p(0),p(1),…,p(mb-1)],将校验比特分为2部分P=[P1P2],其中P1=[p(0)T,p(1)T,…,p(mc-1)T],记为mc组,P2=[p(mc)T,p(mc+1)T,…,p(mb-1)T],记为mb-mc组。
通过基矩阵扩展得到的校验矩阵为H,利用HcT=0,展开得到式(5):
(5)
其中,Hi(i=A,D,O,E,F,I)表示校验矩阵的子矩阵,HA和HD组成核心矩阵,其中HD是准双对角矩阵,HO表示全0矩阵,HI是单位矩阵,那么可得到:
(6)
(7)
要得到校验比特,需要分为以下2步进行。
1)通过使用准双对角矩阵HD的特殊结构,迭代计算出P1;
2)通过P1和单位矩阵HI算出P2。
P1求解的过程也可以分为如下2步:
1)初始化。将式(6)展开后进行累加,得到:
(8)
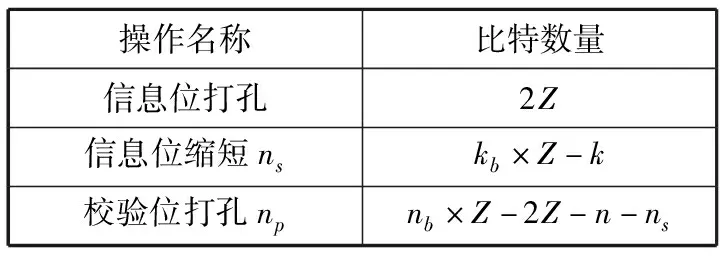
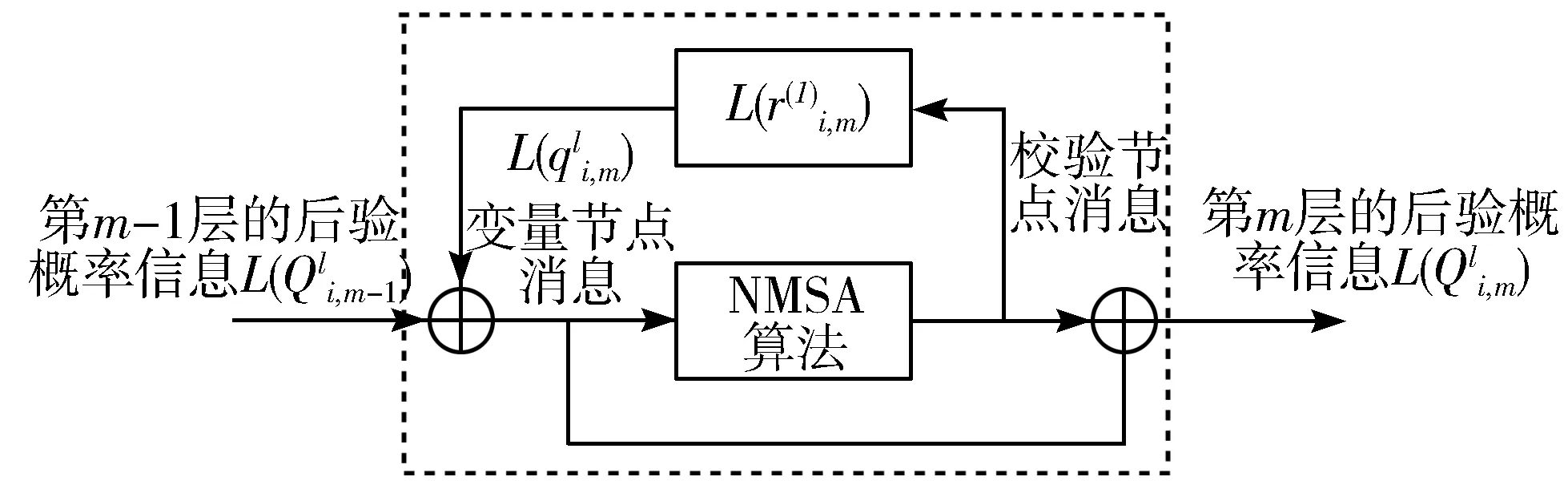
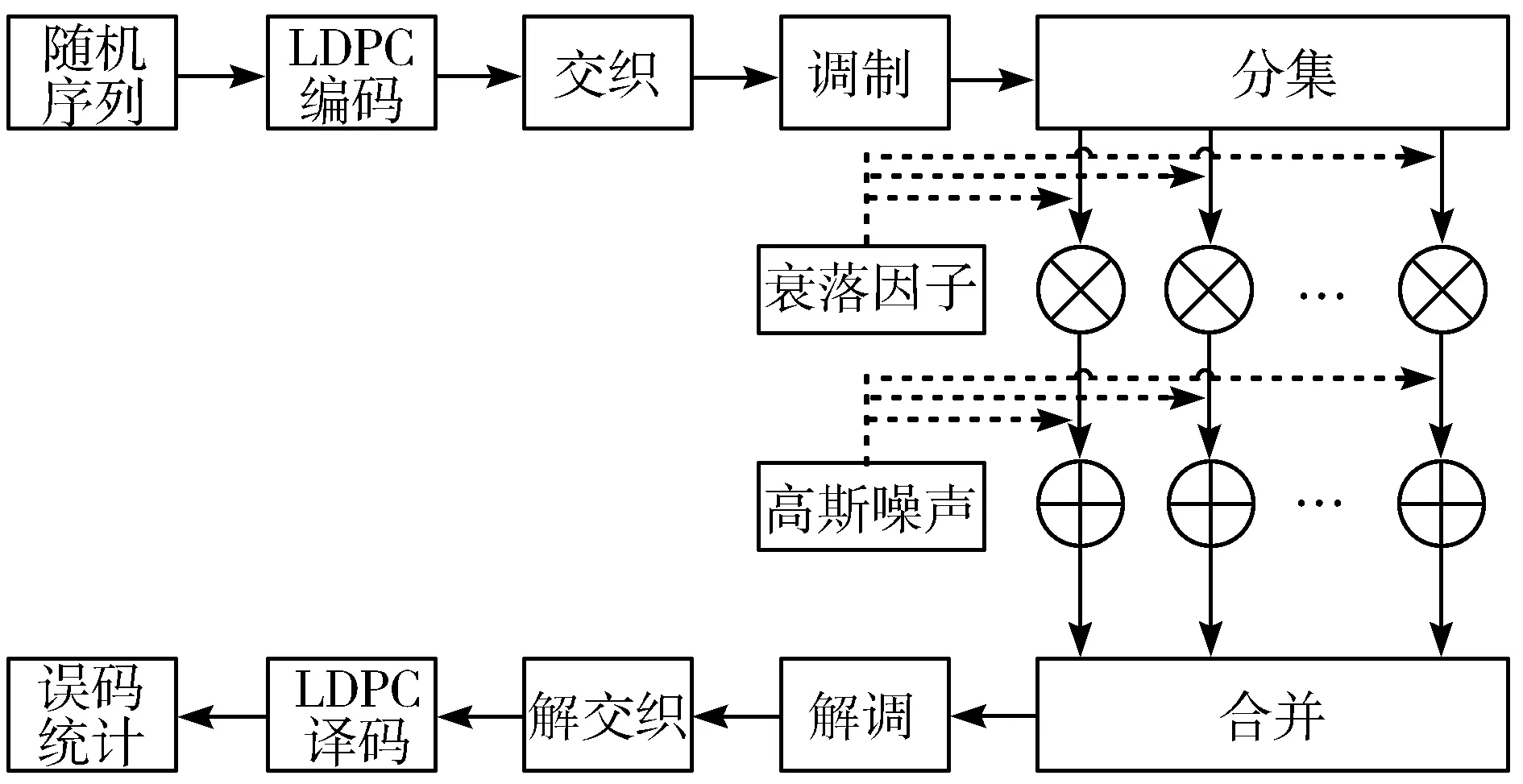
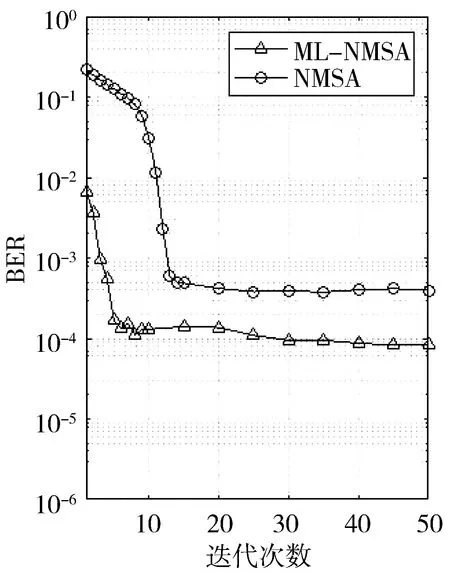
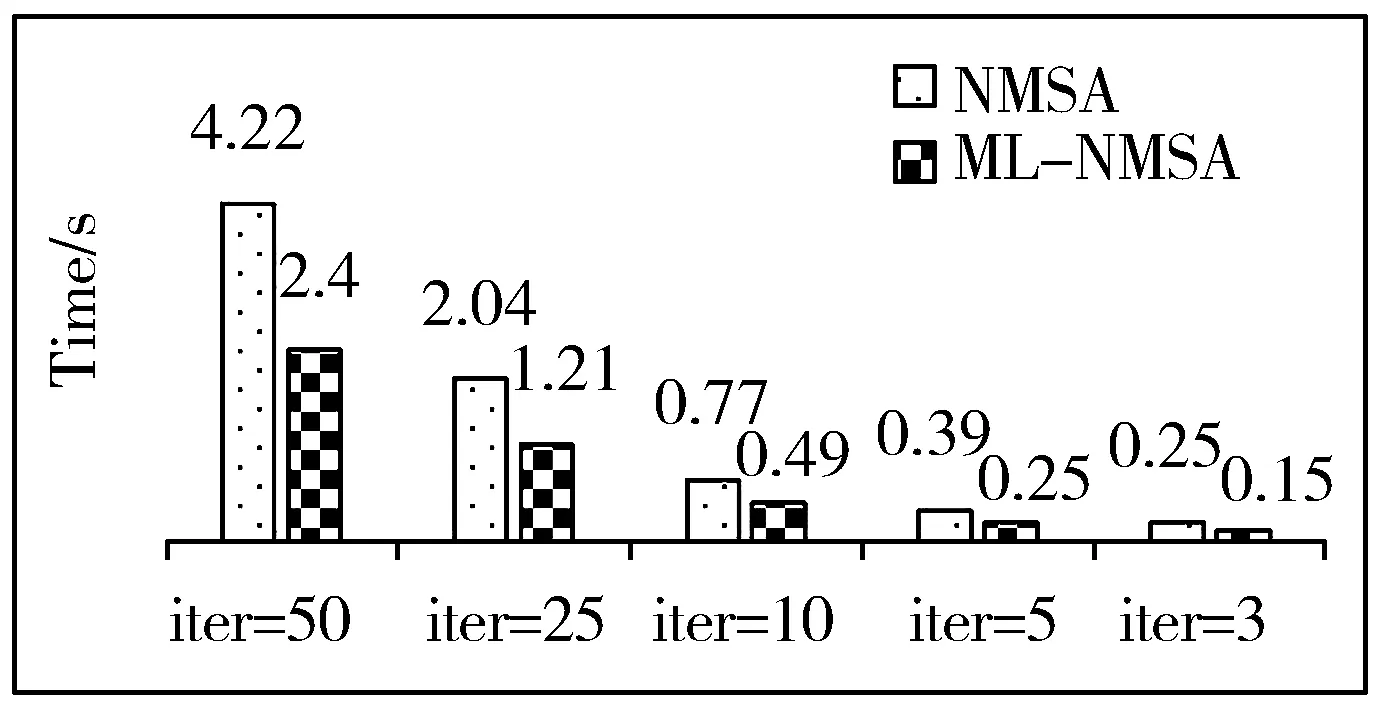
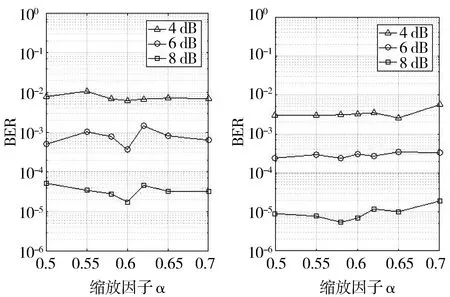
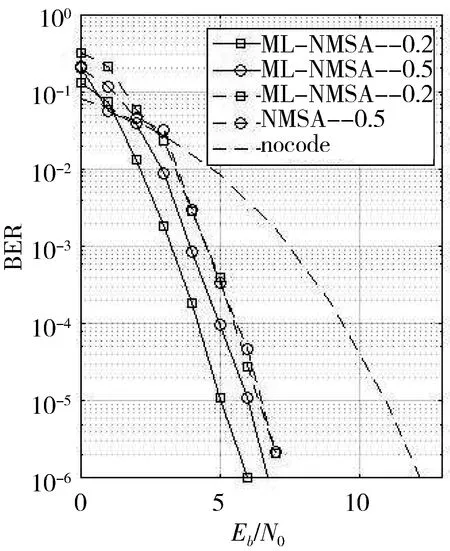
idx(0 (9) 2)迭代。根据HD结构可得到以下表达式: (10) (11) 得到P1后,展开式(7)可得: (12) 求出校验比特序列P=[P1P2],将其与信息比特合并,得到c=[SP]。为了保证任意码长和码率的实现,5G-NR LDPC码采用信息位打孔、信息位缩短和校验位打孔技术[20]。图3给出了5G-NR LDPC码的打孔、缩短和扩展示意图。 图3 5G-NR LDPC码打孔、缩短和扩展示意图 当得到码字c后,对其进行打孔和缩短,打孔和缩短的比特个数如表2所示。 表2 打孔和缩短比特的数量 5G-NR LDPC码采用了打孔和缩短技术,在进行译码前需要通过预处理来补全打孔和缩短的信息位和校验位的最大似然比信息。预处理的步骤如下: 1)前2Z位的被打孔信息位补全为全0值; 2)缩短信息位ns补全为全0值对应的LLR值; 3)被打孔的校验信息位np补全为全0值。 LDPC码的译码算法中[21]最常用的有和积算法(SPA)、最小和算法(MSA)和归一化最小和算法(NMSA)。本文采用归一化最小和算法,NMSA算法相比SPA对于信道估计要求低,译码复杂度更低,相比于MSA算法有更好的误码性能。 分层译码算法属于一种部分并行译码算法,它的基本思想是将一个LDPC码分为多个子码来进行迭代译码,一般将校验矩阵H的行分成若干组,每组看成一层,每组之间采用串行迭代策略,而组内采用常规的全并行迭代策略,组内迭代译码采用上述的NMSA译码[22]。图4为LDPC码的分层译码算法操作框图。 图4 分层译码算法的第m层译码流程图 在分层译码算法中,每完成一个子码的所有校验节点更新后就进行以此变量节点的更新,这样加快了译码的收敛速度。 LDPC码在散射信道下的初始信息比AWGN信道下的初始信息对最终的译码结果有更大的影响[23-24]。初始信息的LLR值的含义是某个变量节点判决为1或0的概率大小,故概率越大,说明某个节点正确判决的概率越大。在传统的NMSA算法中,校验节点的更新如下: (13) 但是,这样会使得缩放因子α对于某些校验节点抑制过度,故引入增益因子λ,来矫正某些抑制过度的节点。 Step1初始化。迭代次数l=1,译码层数m=1,输入的信息为yi。 (14) Step2迭代。按照校验矩阵的行序号进行校验节点和变量节点的更新。 Step2.1对于第m层的每个变量节点,更新先验信息: (15) (16) Step2.3将计算出的校验节点信息进行修正,其中λ=2-α: (17) Step2.4更新变量节点的信息,在每个子层的校验节点更新完成后立即进行变量节点的更新,并将这层的变量节点更新的后验概率输入下一层进行迭代译码。 (18) Step4如果m>T,则l=l+1,m=1,并转至Step2。 图5是本文的散射信道模型的整体设计思路。首先在发射端生成一组随机序列,然后进行LDPC编码,随后将编码后的码元序列传送到交织器中进行交织,调制完成后经过多重分集进入散射衰落信道,接收端接收后送入解调器中解调并合并,然后进行解交织和译码,最后将译码得到的序列和发射端生成的随机序列进行误码统计,之后得到LDPC码在衰落信道中的性能。 图5 散射信道模型的整体设计图 图6给出了在散射信道下Eb/N0=7 dB时,使用8重分集技术,ML-NMSA算法和NMSA算法的收敛性。信息位k为960,码率为1/4,调制方式为BPSK。由图6可以看出,ML-NMSA算法在误码率稳定时的迭代次数为7次,而NMSA算法在误码率稳定时的迭代次数为14次,ML-NMSA算法的迭代次数为NMSA的一半。 图6 ML-NMSA算法和NMSA算法的收敛性 图7给出了完成ML-NMSA算法译码和NMSA算法译码的时间。使用5G-NR LDPC编码,码长k=960,码率r=1/4,缩放因子α=0.8,最大迭代次数(iter)分别为50、25、10、5、3。在同一最大迭代次数下,ML-NMSA算法要比NMSA算法速度提高1.5倍左右,结合图6结论,NMSA算法的迭代次数是ML-NMSA算法的2倍时误码率稳定,ML-NMSA算法完成一次译码的时间是NMSA算法的1/3。 图7 不同迭代次数下,ML-NMSA和NMSA所用时间 对不同的缩放因子α的5G-NR LDPC码的译码性能进行仿真,α的取值与译码后的误码率关系如图8所示。码长k=960,码率r=1/5和1/2,调制方式为BPSK,分集方式为8重分集,取Eb/N0=8 dB,此时误码率达到10-4以下,可以看出码率为1/5,缩放因子α=0.58时,ML-NMSA译码算法性能达到最佳;码率为1/2,缩放因子α=0.60时,ML-NMSA译码算法性能达到最佳。在不同的码率下,缩放因子α的最佳取值存在一定的变化,在进行ML-NMSA算法译码时,需要首先确定缩放因子的值,表3给出BER=10-5时,部分码率下的最佳缩放因子取值。 (a)r=1/2,α与译码性能关系 (b)r=1/5,α与译码性能关系 表3 码率与缩放因子关系表 图9分别给出了16重分集下,5G-NR LDPC码在散射信道中的误码性能。k=960时,选择码率r=1/5和1/2;k=8448时,选择码率r=1/3和2/3。译码采用本文提出的ML-NMSA算法,α的取值为表3中各码率下确定的最佳值,最大迭代次数为25次。 (a)k=960时,不同码率下的误码性能 从图9可以看出,k=960,误码达到10-5,码率为1/5时,ML-NMSA算法误码性能比NMSA算法提升1.4 dB;码率为1/2时,ML-NMSA算法误码性能比NMSA算法提升0.6 dB;k=8448,误码达到10-5,码率为1/3时,ML-NMSA算法误码性能比NMSA算法提升1.2 dB;码率为2/3时,ML-NMSA算法误码性能比NMSA算法提升0.6 dB。 本文研究了散射信道下的5G-NR LDPC码误码性能,提出了一种适用于散射信道的改进分层归一化最小和译码算法,并研究了缩放因子在不同码率下的最佳取值。此外,本文使用的ML-NMSA译码算法,提升了性能,提高了译码速度,降低了译码复杂度,更利于工程应用。
3.2 5G-NR LDPC码的改进译码
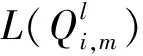
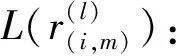
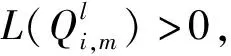
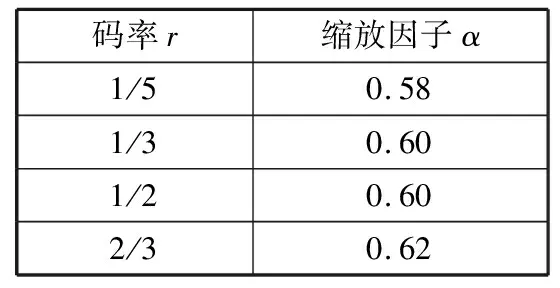
4 仿真结果
5 结束语

