参数微扰法中基态能量与近似级数的关系

吴 锋，孟丽娟

(盐城工学院物理系，江苏 盐城 224051)

参数微扰法通过引入参数重构量子体系哈密顿量中的无微扰项和微扰项，削弱了微扰项的影响，提高了本征能量的准确性，扩大了微扰法的适用范围[1-8].目前，参数微扰法已经成功用于研究三体类氦原子、四体类锂原子和五体铍原子体系[1-6]，这些工作促进了对电子对核屏蔽效应的认识，加深了对电子间相互作用、泡利不相容原理和全同粒子交换对称性的理解.

用参数微扰法精确计算体系能量，有时需要计算到二级甚至多级近似，那么就会遇到和利用微扰法一样存在的困难，即计算包含着无穷项求和的能量修正项.鉴于此，文献[3]利用类氢原子s态波函数构造氦原子的近似波函数，巧妙实现了对氦原子四级近似基态能量的精确计算，理论值与实验值的绝对误差为0.0049 Hartree.但不足的是，该文在构造波函数时牺牲了电子的空间交换对称性，而且计算的氦原子基态能量与采用的近似级数间的关系尚不清晰.为此，本文在构造满足空间交换对称性的近似波函数的基础上，对参数微扰法算出的氦原子基态能量与近似级数间的关系进行了探究，以期为利用参数微扰法精确计算量子体系本征能量提供借鉴.

1 理论和方法

氦原子的非相对论哈密顿算符(原子单位):

(1)

其中

(2)

(3)

式中r1和r2为原子中两个电子到核的距离，r12是两个电子间的距离，Z为核电荷数，σ为反映电子对核屏蔽效应的微扰参数.

根据微扰论，氦原子的零级近似基态能量:

E(0)=-σ2

(4)

基态能量的第i(i=1,2,3,)级修正[1,9]:

E(i)=〈ψ(0)|H′|ψ(i-1)〉

(5)

其中，ψ(0)为零级近似波函数，ψ(i)为第i级修正波函数，与ψ(0)正交.根据式(2)结合氦原子特征，选取类氢原子的ns (n=1,2,3,)态归一化波函数:

(6)

(1F1为合流超几何函数)构造ψ(0)和ψ(i)：

ψ(0)=ψ1s(r1)ψ1s(r2)

(7)

(8)

氦原子的多级近似基态能量和波函数分别为:

E=E(0)+E(1)+E(2)+E(3)+…

(9)

ψ=ψ(0)+ψ(1)+ψ(2)+…

(10)

由式(7)和式(8)可知，ψ自动满足空间交换对称性.E和ψ中参数σ由基态能量取最小值确定.

2 计算结果和讨论

利用Mathematica软件的符号计算功能，得到氦原子各级近似基态能量E的解析表达式(限于篇幅未列出)，它们是参数σ的函数.在讨论近似级数对E值的影响时，既可以通过对各级近似基态能量分别取最小值确定σ，也可以通过由某级近似基态能量取最小值确定σ，然后在各级近似计算中保持不变.下面分别进行讨论.

2.1 σ分别由各级近似能量取最小值确定

表1列出了2级至12级近似基态能量E，参数σ，以及E与实验值[10](-2.903386 Hartree)的绝对误差|ΔE|.可以看出，E随着近似级次i的增加而减小.图1进一步给出了各级近似基态能量E相对前一级基态能量的改变量.可见，E的改变量随着i的增加越来越小，逼近于零.

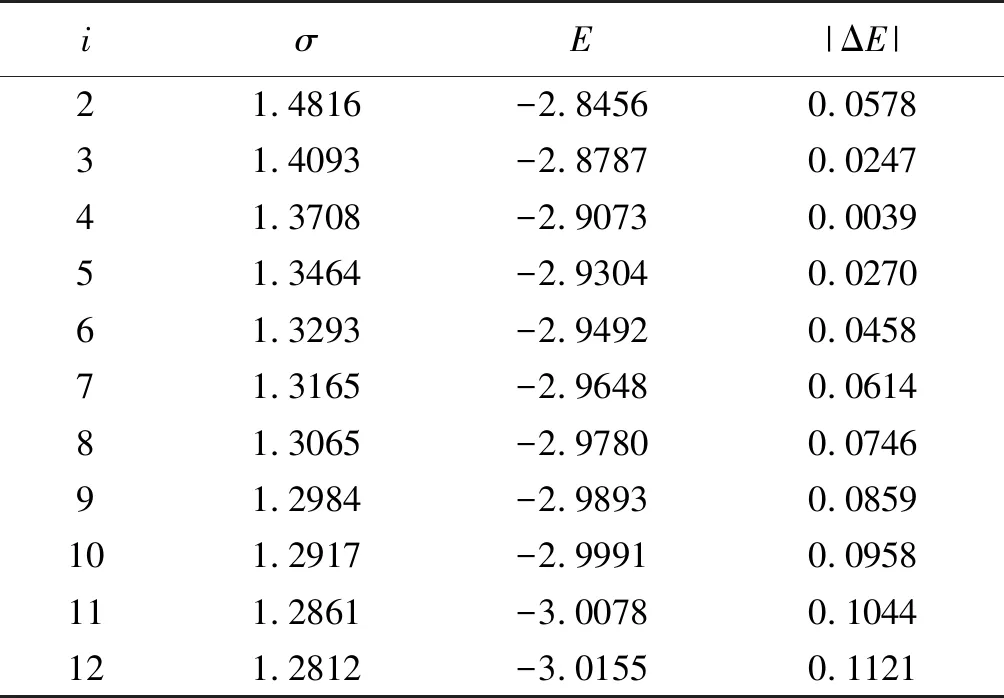
表1 氦原子i级近似基态能量E及其与实验值的绝对误差|ΔE|(原子单位)

其次，从表1末列数据，可以看出，|ΔE|随着i的增加先是减小，i=4时达到最小，然后又逐渐增大.这表明，氦原子基态能量与实验值的绝对误差随着i的增加存在一定起落.这与文献[3]提出的|ΔE|随着i的增加越来越小的论断不同.因为|ΔE|存在起落，所以需要合理选择近似级数，提高氦原子基态能量计算值的精确性.例如，表1中4级近似的|ΔE|仅为0.0039 Hartree.

图1 i级近似基态能量相对前一级基态能量的变化

2.2 σ由某级近似基态能量取最小值确定，并在各级近似计算中保持σ相同

将表1中各级近似得到的σ数值作为固定值，分别同时代入氦原子2级至12级近似基态能量表达式，所得数值结果按从左到右顺序分别列于表2.分析E的每一列数据可知，E随着i的增加仍有与2.1节相同的变化规律，即逐渐减小，改变量越来越小(如图2)，与实验值间的绝对误差|ΔE|有起落.另外，σ的变化对|ΔE|的起落产生影响.所以，除了选取合适的近似级数计算基态能量，还需选取合适的近似级数确定σ，才能得到更为精确的氦原子基态能量.例如在σ=1.3165时，4级近似基态能量-2.9027 Hartree，与实验值的绝对误差小至0.0007 Hartree，结果相当精确.

表2 σ恒定时的i级近似基态能量(原子单位)

图2 在σ=1.3165时，i级近似基态能量相对前一级基态能量的变化

3 结束语

在构建满足空间交换对称性波函数的基础上，利用参数微扰法对氦原子基态能量进行了计算，并根据微扰参数的两种确定方式，分别对基态能量与近似级数的关系进行了分析.研究发现，氦原子基态能量随着近似级数的增加，逐渐降低，改变量越来越小，基态能量与实验值的绝对误差存在一定起落.选择合适的近似级数确定微扰参数及基态能量，对提高氦原子基态能量计算值的精确性具有重要作用.