受迫振动非线性特性的教学拓展

丁红胜，王佳曦，张师平，董军军

(1. 北京科技大学 数理学院应用物理系，北京 100083；2. 北京科技大学 自然科学基础实验中心，北京 100083)

振动是一种普遍存在于客观世界的物质运动形式，系统在周期性外力的持续作用下的振动即为受迫振动[1]．波耳共振仪是高校物理实验教学中研究受迫振动运动规律较为普遍的仪器，也是学者探讨较多的实验项目[2-4]．实验测量中，仪器的轴承摩擦和弹簧非线性效应的影响是造成实验数据偏离预期的主要因素．如果在受迫振动的分析中考虑这两种因素的影响，则非常有助于学生理解实验原理和结果偏差．本文基于受迫振动常规实验，延伸探讨其非线性特性，通过Matlab数值分析的方法来研究杜芬方程的混沌特性，以此提高学生对受迫振动的认知，并加深对其非线性特性的理解．

1 受迫振动

1.1 受迫振动方程

波耳共振仪[5](如图1所示)的摆轮可在弹性力矩作用下自由摆动，若同时加上阻尼力矩和驱动力矩，摆轮可做受迫振动．

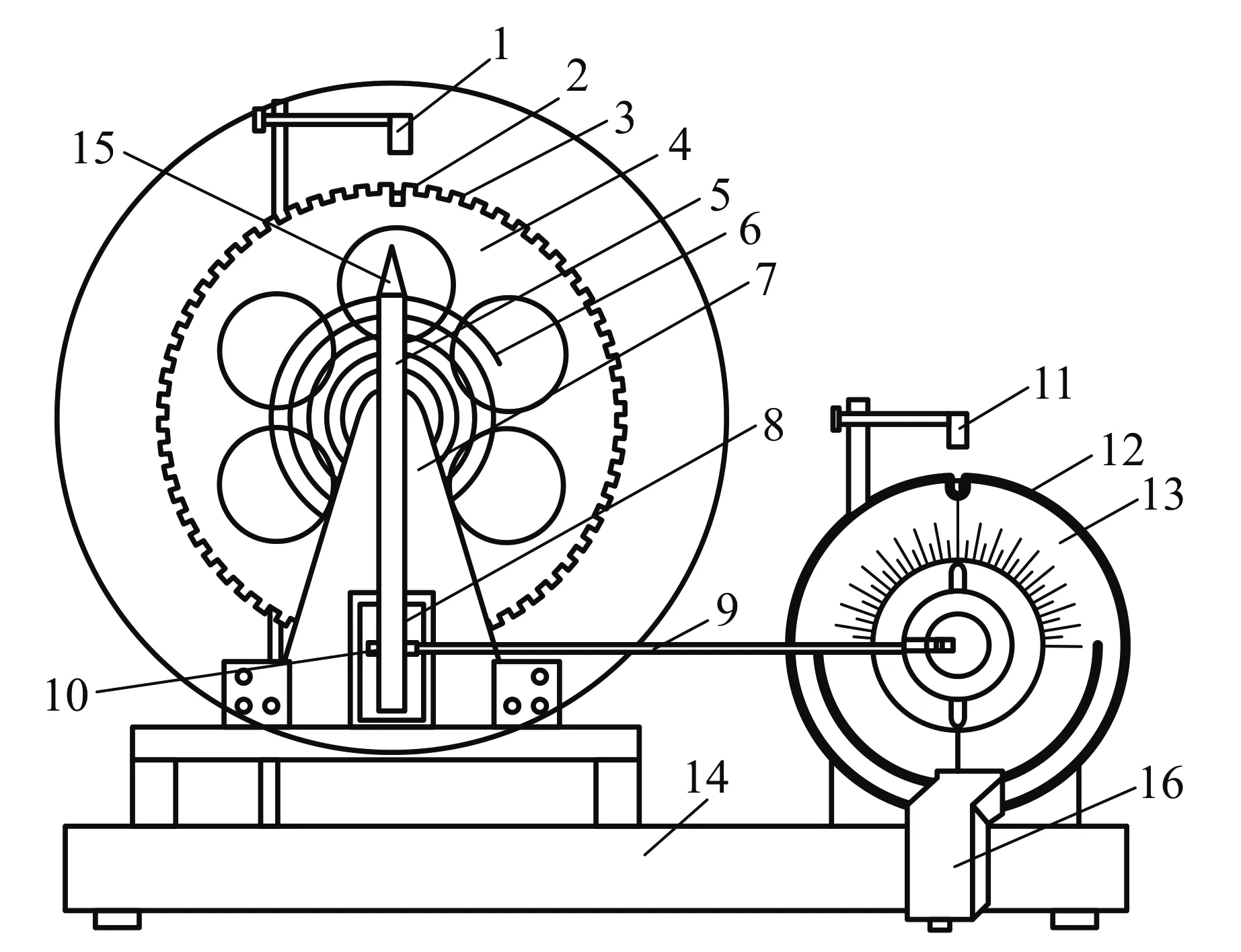
1. 光电门A；2. 长凹槽；3. 短凹槽；4. 铜制摆轮；5. 摇杆； 6. 蜗卷弹簧；7. 机架；8. 阻尼线圈；9. 连杆；10. 摇杆调节螺丝； 11. 光电门B；12. 角度盘；13. 有机玻璃转盘；14. 底座； 15. 弹簧夹持螺丝；16闪光灯图1 波耳共振仪的结构示意图[5]

(1)

式中，J为摆轮的转动惯量，-kθ为弹性力矩，k为弹簧的劲度系数，M0为驱动力矩的幅值，ω为驱动力的角频率．

(2)

当mcosωt=0时，即在无周期性外力矩作用时，式(2)为阻尼振动方程；当阻尼系数为零，即无阻尼时，式(2)为简谐振动方程，ω0即为振动系统的固有频率．

方程(2)的通解为

θ=θ1e-βtcos(ω1t+α)+θ2cos(ωt+φ)

(3)

通解含有两个部分：θ1e-βtcos(ω1t+α)表示阻尼振动，随着时间的演化，振动会逐渐衰减，直至忽略不计；θ2cos(ωt+φ)表示简谐振动，驱动力矩持续对摆轮做功，振动系统接收驱动力所传送的能量，使振动系统最终达到一个稳定的状态．

振幅为定值，

(4)

系统相位差为

(5)

由式(4)和式(5)可看出，稳定振动时，驱动力的幅值M0、阻尼系数β、驱动力的频率ω(或驱动力周期T)和系统固有频率ω0(或固有周期T0)4个参量共同决定系统振幅和相位差的大小，与振动的起始状态无关．

(6)

可以看出，阻尼系数越小，驱动力的角频率越接近系统的固有角频率，振动幅值也越大．

1.2 阻尼系数、固有周期、固有频率的测量

实验中通常选择阻尼开关位置为2，将波耳共振仪有机玻璃盘上零度标志线对准0°，用手将摆轮转动至140°～150°之间，放手后控制箱会自动连续记录摆轮完成阻尼振动10次的振幅θ0～θ9．数据如表1所示．

表1 阻尼系数测量数据

选择“自由振荡”进行测量，将有机玻璃盘上零度标志线保持在0°，用手将摆轮转动至140°～150°之间，放手后记录每次振动振幅值及其相应周期，并计算相应频率值．数据如表2所示．

表2 振幅、周期、频率关系数据

2 受迫振动方程非线性修正

2.1 弹簧非线性效应

一般情况下，可以认为弹簧的劲度系数k为常数，但是在上述弹簧自由振动的实验中，通常随着振幅的减小，振动系统固有周期会逐渐增大，这意味着振动系统的弹性回复力随着振幅的减小而减弱[2]．因此不妨假设弹簧的劲度系数为振幅的函数k=k(θ)，则回复力矩为

Fk=k(θ)θ

(7)

将Fk=k(θ)θ进行泰勒展开至一阶项，

(8)

(9)

2.2 轴承摩擦效应

轴承摩擦效应普遍存在于定轴转动的运动中，当轴承转动速度较小时轴承静摩擦力较大，而当转速达到一定临界值后，轴承摩擦力将保持稳定[6]．

实验发现，轴承摩擦力随轴承角速度的变化率较缓，因此可采用二次函数的形式来描述轴承摩擦力矩随角速度的关系

(10)

其中，固定系数B>0，C>0，在此情况下，即表明摩擦力矩随角速度的增加而缓慢降低．

2.3 阻尼振动方程非线性修正

综合弹簧的非线性效应与轴承摩擦效应对振动方程的修正，可以得到修正后的阻尼振动方程为

(11)

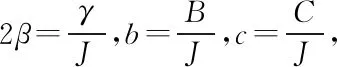
(12)

式(12)即为非线性项修正后的阻尼振动方程，是一个待定系数的二阶微分方程．

在此情况下，基于Matlab软件，用数值方法计算其数值解，通过多次给定a、b、c的数值进行模拟计算，拟合阻尼振动实验所测得的数据．

(13)

利用Matlab软件内置的ode45函数，根据四阶龙格-库塔法，多次变步长数值积分，可以得到，当待定系数满足a=0.014,b=0.002,c=0.005时，数值方法解得的阻尼振动方程与实验数据拟合的最为接近，特别是在振幅为90°～140°时，弹簧形变较大，弹簧非线性效应较为明显的区域．

图2中指数曲线为阻尼振动的振幅-时间实测数据的拟合曲线，周期性曲线为非线性微分方程的数值解．

图2 阻尼振动数值积分与拟合曲线

2.4 受迫振动方程非线性修正

在修正后的阻尼振动方程(12)的右边加上一个周期性力矩，即为受迫振动方程，

(14)

该方程中m为未知参量，需要通过实验仪器进行数据测量加以确定．

选取“阻尼2”档位，打开电机，设定在某一转速，当观察到摆轮的受迫振动周期与电机的周期趋于一致时，即受迫振动达到稳定时，开始测量．读出每次摆轮受迫振动的幅值θ和驱动力矩每10次振动周期10T，利用频闪法测量摆轮受迫振动的位移与驱动力之间的相位差φ，并记录此时电动机的转速值，结果如表3所示.

表3 幅频特性与相频特性测量数据

至此获得了在一定情况下，受迫振动动力学方程的全部参量：ω0=3.775 rad·s-1，β=0.081，m=1.02，a=0.014，b=-0.002，c=0.005．

(15)

把上述一阶微分方程组输入程序，利用数值积分求解其动力学特性，结果如图3所示．

图3 系统时间响应与相平面曲线

图3中左侧为受迫振动系统的时间响应曲线，右侧为系统的相平面曲线．受迫振动系统的时间响应曲线表示了振动振幅随时间变化的特性，可以看出，随着振动时间的增加，振动频率逐渐稳定，振幅逐渐增加直到最大值并且保持稳定．

受迫振动系统的相平面曲线图表示了速度随振幅变化的关系．可以看出随着时间的增加，速度与振幅也会趋近一个稳定状态．

如果改变其中的一个参量，例如将与弹簧非线性效应相关的参数a从0.014调整为10，采用同样的方法对系统进行数值分析，得到的结果如图4所示．原本稳定的受迫振动系统在振动后期开始出现一定的随机运动，即混沌现象．

图4 系统时间响应与相平面曲线

基于波耳共振仪的受迫振动，由于其振动方程中涉及的非线性项偏多，不利于定性和定量分析受迫振动系统中的混沌现象，因此可以选择典型的非线性受迫振动方程——杜芬方程进行探讨．

3 受迫振动方程的混沌

3.1 杜芬方程

振动问题中的很多数学模型都可以通过转化为杜芬方程来进行研究和分析，杜芬方程是研究和分析某些非线性动力学系统的基础．

杜芬方程[7]的标准形式为

(16)

其中，δ>0，g(x)是含x3项的函数，f(x,t)是周期性函数．

标准化后的杜芬方程称之为杜芬系统．杜芬系统是一类从简单受迫振动的物理模型中归纳出的非线性振动系统模型，形式简洁，具有代表性，其应用范围十分广泛．许多动力学过程都与杜芬系统的模型极其相似，比如化学键的断裂、建筑结构的震颤和轮船的横摇运动、电路周期振荡、电路信号检测、电路系统模拟分析和电路的故障检测等等．

3.2 硬弹簧型杜芬方程

杜芬方程一般可以分成四种基本类型，可以选取其中的硬弹簧型杜芬方程[8]进行探讨，

(17)

将式(17)转化成一阶微分方程组：

(18)

其中ω、f、a、β、c为可变参量．

给定不同的初始条件，利用数值计算的方法来分析硬弹簧型杜芬系统的受迫振动．

当振动时间为300 s时，结果如图5所示，从上至下依次是不同f取值下的系统时间响应图、系统相平面轨迹图、系统功率密度谱．

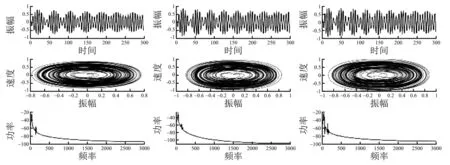
图5 系统时间响应、相平面轨迹、功率密度谱随f值的演化

由图5可以看出，随着系统参量f的变化，系统逐渐由周期性运动进入混沌状态．

3.3 杜芬方程的混沌

从图5的相平面轨迹图可以看出，系统从只有一个相对稳定的平衡位置(原点)，逐渐变为具有两个相对平衡的位置(焦点)，这体现了无序混沌状态中存在一定程度上的有序特性．相平面轨迹图中相对平衡位置发生改变的同时，相轨迹也从圆形逐渐转化为类似于莫比乌斯环的椭圆形状．进一步推测，系统会拥有两个相对平衡的焦点，相轨迹围绕这两个焦点运动，而且可将这两个焦点类比为三维非线性系统中奇异吸引子[9]，如图6所示．

图6 奇异吸引子

奇异吸引子是混沌系统中独有的一种吸引子，也被称之为混沌吸引子，它代表着混沌状态中的一种定态．具体表现在系统从任一初始状态开始，最终都会被奇异吸引子吸引到相空间中的某一特定区域．奇异吸引子与一般吸引子有所区别，当混沌状态的轨迹线进入奇异吸引子之后，轨迹线并不会像一般吸引子一样，吸引轨迹线继续围绕其运动，最终形成一个相对封闭的图形，而是会让两条接近的轨迹线发生指数分离．从系统外部看，奇异吸引子是在聚集轨迹线；从系统内部看，是轨迹线发散的过程．奇异吸引子常常成对出现，两个奇异吸引子同时对轨迹线的作用，共同构筑了混沌系统一定程度上的有序性．

图7 从左至右分别为f=1, f=3, f=5时的相空间轨迹线

从图7可以看出，杜芬方程中的两个焦点在含有时间项的坐标下，展开成了两条轴线，体现了其时间平移不变性，参量f的变化引起相空间轨迹明显改变，表明混沌系统对参量具有很强的敏感性，但在速度-振幅的相平面轨迹图中，两个焦点是稳定的，不随时间发生变化，这与奇异吸引子的性质非常类似．

4 结论

基于波耳共振仪受迫振动实验，探讨其中的非线性影响因素，对阻尼振动方程进行修正，考虑轴承摩擦和弹簧非线性效应，结合Matlab数值计算结果与波耳共振仪实测数据，确定波耳共振仪系统的非线性项参数，分析其非线性效应．通过引入非线性理论的思想和数值分析的计算方法，有助于学生准确认知实验现象，加深对实验原理的理解．

为了丰富实验教学内容，引入弹簧型杜芬方程，分析其非线性特性，利用数值计算方法探讨受迫振动模型进入混沌状态的条件及其运动特性．受迫振动是否会进入混沌状态，可以根据系统响应时间曲线(振幅-时间)、系统相平面曲线(速度-振幅)和功率密度谱曲线(功率-频率)综合判断．如果受迫振动做周期运动，其响应时间曲线会呈现规则的周期性，其相轨迹图具有极限环的特性，其功率图谱峰值呈现离散的状态；如果系统进入混沌状态，其时间曲线会具有无规则的、类似于噪声的特性，其相平面曲线在有限区域内是无周期性的，随着振动时间的延长，其轨迹线会逐渐铺满整个区域，功率图谱含有多个峰值；如果系统的响应时间曲线和相平面曲线在上述两种情况之间，则功率图谱呈现离散状态，系统做的是拟周期运动，如果改变它的系统参量或者初始条件，则有可能转变为周期运动或混沌运动．一般情况下，受迫振动受非线性效应影响越大，最终进入混沌状态的可能性越高．