关于一维量子散射中一些问题的简单说明

应文祥，彭凯玥，曹 龙

(中国科学技术大学 化学物理系，安徽 合肥 230026)

一维方势垒穿透是本科量子力学课程的一个重要内容.大多数教材采用求解定态薛定谔方程的方法[1-4].它本质是个一维定态散射问题(如无特殊说明，本文均指定态弹性散射)，我们也可以求解一维Lippmann-Schwinger方程——这是一种更普适的方法，理论上可以程序化解决任意形状势垒的一维散射问题.早在2001年，陆晓[5]就补充了这种思路，并通过迭代求出了反射、透射概率幅，但是其过程的数学存在瑕疵.王琴惠[6]在2004年给出的求解过程数学上没有问题，但透射、反射系数项中仍含有ψ(x)，须通过代入试探解来求解实际问题.

鉴于前人对一维散射问题处理方法的一些理解误区，本文给出了较为清晰的数学推导和说明.简单讨论了迭代法求解一维Lippmann-Schwinger方程的手续，指出前人的错误.

1 一维散射问题常见处理手法的简单讨论

一维散射问题的定态薛定谔方程为

(1)

最常规的思路就是直接求解一维定态薛定谔方程.参考文献[1]中列举了很多种一维可解势——对于这类势函数，可以解析求解.但局限性是，这不是一种通用的方法.对复杂的势函数V(x) 很难解析求解薛定谔方程.例如一维有限深方势阱[2]，薛定谔方程为超越方程，无法写出解的显示表达式.

第二种思路仍然是处理微分方程，但略有差异.对薛定谔方程做变量代换：

(2)

则薛定谔方程形式简化为

(3)

可以发现这是个二阶变系数齐次线性方程，并且属于下面这种类型：

y″+r(x)y=0

(4)

因此只要能够一般化处理 (4) 这种类型的二阶变系数齐次线性方程，写出通解并代入边界条件，则问题可以完全解决.基于这种思路的相关研究也有不少[7-10]，但是依旧存在困难和局限性，有时需数值求解[8].能够写出通解的仅是一些特殊情形[9,10].

第三种思路见参考文献[4].作者Franz Schwabl把任意形状势垒分成无穷多个窄的一维方势，并且认为总透射系数是这些小方势的透射系数之积.这是一种粗糙的数学处理，难以保证计算的可靠性.这里指出两点问题.其一，Franz使用如下近似公式 (5) 处理每小段的一维方势：

(5)

但是该近似是对于高且宽的势垒才成立的[2].其二，按照这种模型，可能存在粒子在势垒内部经过多次反射、透射后最终通过势垒的情况.

还有不少其他处理思路，例如相移分析[11,12]等，还有人开发了处理一维耗散问题(非弹性散射)的方法[13]，在此不一一列举和讨论了.

通过Lippmann-Schwinger方程来处理一维散射问题是一种很好的思路[5,6,14,15].方程可以基于式 (3) 通过格林函数方法导出[6,15,16]，这里不再花费篇幅介绍.一维的Lippmann-Schwinger方程形式如下

(6)

其中G(x,x′)为一维非齐次亥姆霍兹方程边值问题的格林函数解：

(7)

把代换的变量代回，式(6) 也可以写成如下形式：

(8)

此方程为积分方程，无法直接求解，一般要借助于迭代算法.记

(9)

并把积分写成分段式以去掉绝对值

(10)

ψ(x) 为全空间上的解.考察ψ(x) 的渐进行为,当x→ +∞ 时， 有

(11)

2 对参考文献 [5]误区的说明、拓展讨论

2.1 迭代法和代入试探解法

参考文献 [5] 给出波函数的渐进行为是正确的，对应一维散射问题的边界条件.但是，作者错在使用渐进解迭代，混用了迭代法和代入试探解法.作者首先使用迭代法，并认为经过多次迭代后的真实解就是

ψ(x)=sAeikx

(12)

(见参考文献 [5] 式 (19) ，其中s为透射概率幅)，这是错误的.这种做法就相当于代入试探解，但是这个解的形式又太简单，不能包括x轴上波函数的全部信息——式 (12) 形式的波函数仅仅能够描述无穷远处波函数的行为，而Lippmann-Schwinger方程中的ψ(x)为全空间的波函数，导致错误.例如可以检验，参考文献 [5] 给出的理论无法对一维方势散射给出正确结果.

一般来说，迭代法和代入试探解法都可以解方程，但是参考文献 [5] 的作者此处混淆了这两种方法.如果迭代，就不能随意舍去波函数的重要信息，要考虑全空间范围，从低阶到高阶一步步进行，最终会收敛于真实解；如果代入试探解，那么为得到正确结果，这个试探解必须包括该束缚定态下所有可能的物理态——即：全空间范围内的解，包括势垒内部、外部，进而确定试探解的前系数.如前文所述，如果仅仅代入无穷远处的渐进解，就会缺失大量信息，特别是如图1所示势垒内部的波函数的真实态——这是问题的难点.

图1 散射问题图示说明[17]

迭代法求解Lippmann-Schwinger方程时，迭代次数对应玻恩近似的阶数[18].并且，一维散射问题引入玻恩近似将不受“低能散射”条件[18]的束缚，因为根据弹性散射问题的边界条件，无穷远处入射波和透射波的波矢相等，因此不存在高维情形时由于波矢方向变化带来的额外的相位差.高阶玻恩近似能够较好地描述波函数的行为.后面我们给出的例子将说明这一情形，在高能段玻恩近似的结果更好.而低能段可能出现由于截断导致的红外发散.

2.2 S矩阵，反射、透射系数

一般在高维散射问题中，问题可化为求解时间相关的散射S矩阵.求解S一个很好的方法是微扰展开法，可以用戴森级数加以表示[19].基于此，本文一位作者曾提出由式 (11) 进行迭代，并引入相应正规乘积算符[19]——位置编序算符加以表示以统一积分上限

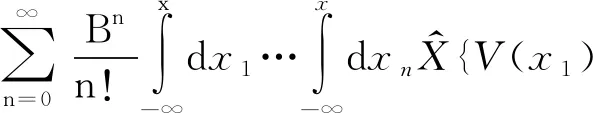
V(x2)…V(xn)}≡

(13)

定态问题不含时，位置算符两两对易，所以去掉编序算符.这种方式给出的s也是错误的，错在用近似了的积分方程迭代，因此只能给出极限形式的s，而真实的s可能会非常复杂.事实上式 (13) 就是一维情形的s的戴森级数表示，只是把时间序列改为空间序列(无本质差别，但时间编序不能直接去掉编序算符).

继续考察一维散射的反射、透射系数.假设粒子从一个方向入射

(14)

其中s为透射概率幅，r为反射概率幅.对于给定的定态势函数，r、s均为复常数.参考文献 [5] 在原文式 (13) 处给了两者之间存在关系式s= 1 +r.这也是错误的.r、s之间的关系由波函数的边界条件确定.例如一维δ势、一维阶梯势等，x= 0 的左侧和右侧分别对应波函数的两个渐进解，在此处根据连续性条件令x= 0，即可直接得出s= 1 +r.但是对于复杂一些的情形例如一维方势散射，此关系式不再成立，由更复杂的边界条件给出r、s之间的关系.笔者猜测，作者此处是想寻找r、s与更高维量子散射中R、S矩阵之间的联系.量子散射的S矩阵是描述无穷远处散射态的厄米算符，反应矩阵R是人为引入的，定义两者关系R+ 1 =S，是为了更方便地导出跃迁几率[17,20].但是退化为一维情形时，R、S并不对应着反射、透射概率幅r、s.一维的S作用在入射初始态上，仍然将给出所有的散射态——包括反射波和透射波，而不仅仅是透射概率幅s所描述的透射波.而一维情形中弹性散射的粒子数守恒关系T+R= 1是根据概率守恒得证的[21].

2.3 势函数积分的敛散性

由于代入的是渐进解，式(13) 只是正确的s的表达式的一部分，其中含有对势函数V(x) 的多重积分.为使得对应的s有意义，我们不得不考虑该积分的敛散性问题.例如对于一维幂函数势：

(15)

当幂指数ν在 (0 ,1 ] 内时积分发散，迭代发散，无法给出透射概率幅.我们在构造势函数时，要构造正规势函数，例如尽量避免涉及无穷奇点等.总之使得s是有意义的.另外，对于这类因为有无穷间断点导致积分发散的情形，张永德给出了很好的观点[22]：这种情形是人为的定义造成的，物理实际上并不存在，我们不必过于纠结由于这类非正规势函数性质带来的不必要的困惑.

推广到更一般的情形，如果使用微扰展开来求S矩阵，在把全哈密顿量分为自由粒子部分哈密顿量H0和相互作用部分V时，就涉及H0选取的问题[19].散射理论中H0并非通常微扰意义下的，选取的H0及其本征态要求包含所有可能存在的物理态，例如平面波、势垒中的束缚态等.正如S.Weinberg在其《量子场论》第一卷中指出[19]，需要使得H0和全哈密顿量H有相同的频谱，H中的任何相关束缚态都应该像一个基本粒子一样被引入H0.由此H0的谱中也可能包含一些束缚态(非平面波)成分；由此也要求了势函数满足相关条件,例如一定的渐进行为等等.

3 应用：一维δ势散射的迭代法求解

一维δ势散射问题，代入试探解的方法可见参考文献 [6]，此处对迭代法举例说明.势函数：

V(x)=λδ(x)

(16)

λ为参数.把式 (16) 代入式 (10) ，并根据δ函数的积分性质得

(17)

下面使用迭代法求解，迭代关系为

(18)

0 阶近似为自由平面波：ψ(0)(x)=Aeikx.此时0 阶透射概率幅：s(0)=1.

把自由平面波ψ(0)(x)=Aeikx代入式 (18) 右边即得一阶玻恩近似结果：

(19)

s(1)=λB+1

进一步迭代可以给出

(20)

s(2)=λB(λB+1)+1

等等.可以注意到透射概率幅有递推关系：

s(n)=λBs(n-1)+1

(21)

当n取无穷大时s已经收敛.把B代换回去，可以反解出一维δ势散射的透射概率幅为

(22)

从而透射系数为

(23)

与文献中代入试探解得到的结果[6,14]完全一致.

下图2 给出了透射系数的前几阶玻恩近似结果，并与解析解进行比较.

图2 δ势散射问题的前7阶玻恩近似下透射系数随入射能量变化情况，以及与解析解的比较.Bn表示第n阶玻恩近似的结果，加粗线条为解析解.这里相关参数取自然单位制：λ= 1,m=1,ћ=1

对于更为复杂的势函数例如一维幂函数势[5]、一维高斯型势垒[8]可借助计算机通过上述固定步骤数值求解.

4 总结

解决一维定态势散射问题，几种方法各有优劣.对于势函数简单的情形，例如一维方势、一维阶跃势等，我们容易给出正确的试探解的形式，此时直接代入试探解求解定态薛定谔方程更方便；对于势函数复杂而无法解析求解的情况，考虑迭代法，数值求解 Lippmann-Schwinger方程.