自行车系统的计算机模拟

姜星宇

(同济大学 电子与信息工程学院，上海 200092)

从自行车发明以来，其稳定的原理一直是人们关注的内容.R.S.Hand在其著作中对自行车稳定性做出了定义:若自行车能够经过垂直其运动方向的扰动后，倾斜角θ与操纵转角β渐进地趋于竖直平衡运动，就是稳定的[1,2].David E. H. Jones在1970年发表的The Stability of the Bicycle[3]中通过制作无法骑行的自行车过程中指出，在自行车的稳定性上，陀螺的稳定效应并不是影响自行车平衡的主要因素，至少不是全部因素. 而前轮的几何因素对中心高低的影响对于稳定性也是十分重要的. 由于两个非完整约束使自由度从无穷小时间内的三个变成有限时间内的七个，加之前轮与车架之间具有十分复杂的的非线性几何关系，因此解出严格的解几乎是不可能的. 许多研究便对于模型进行了线性的简化或者是只考虑其中某些广义坐标，或者半定量地讨论. 例如通过只考虑平衡位置附近的微小扰动将约束方程与拉格朗日函数简化，最后得到线性微分方程[2]. 亦有将前叉设置为与轮心连线垂直的简化方法[4].

对于自行车稳定性的分析也具有一定的实际意义. 关于自行车的自动化也就是无人操控保持平衡有不少研究[4,5]，这也是未来将交通工具智能化的趋势. 而要做到这一点，首先就要分析其平衡的条件与原理.

在不能将其力学原理完全精确地计算出，直接实验又限于成本与时间时，近似求解数值解对于研究自行车的稳定性显得十分重要.本文以拉格朗日方程为基本原理，从分析力学的角度对自行车系统近似计算与分析.

1 基本原理

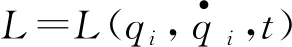
(1)

将第一项展开也就是

(2)

其中cαi为坐标的函数，λα为约束力变量. 为使约束方程中出现二阶导，将约束方程求导:

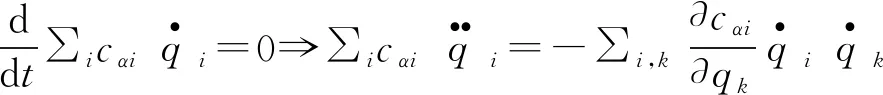
(3)

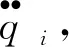
要注意的是，初始条件一定要满足约束，如果不满足，那么约束方程右端就会是一个由初始条件决定的非零常数，而这往往不是我们所需要的.

2 方法验证

根据上述讨论，我们将近似计算方法运用到任意存在约束的力学系统当中，求解拉格朗日方程. 对于不同的系统，计算过程唯一的区别就是函数的形式，因此很方便利用计算机求解. 而对于参数，根据力学相似性可以进行归一化，因此下面的讨论均不考虑系数与单位的问题. 先以傅科摆验证方法的可行性.

在旋转非惯性系下的球面摆是一个完整约束. 以x轴为东，y轴为北，惯性系中速度vabs=v+Ω×R0+Ω×r，那么拉格朗日函数为

图1 北极处傅科摆x-y图及周期(Δt=0.01 s)

表1 傅科摆周期随纬度的变化

3 自行车系统的分析

3.1 轮的约束与动能

为了研究自行车系统的运动，我们先来分析一下轮的纯滚动. 轮的纯滚动通常是一个非完整约束，它满足接触点速度为零，即drC+dφ×r=0. 其中rC为圆心位矢，φ为轮的角速度，r为轮上一点相对于圆心的位矢.

现将轮简化为厚度远小于半径，对称的平面刚体. 它可以用质心坐标(x,y,z)与轮主轴欧拉角(θ,φ,ψ)来描述.
图2显示，θ对应的是轮与水平面的夹角，φ对应的是轮平面与水平面交线与x轴的夹角，而ψ为自转角. 根据垂直轴定理，I3=2I1=I. 对应的动能为

(4)

轮的约束为vC+Ω×r0=0 (vC为质心速度，r0为接触点相对圆心的位矢) ，3个分量为：

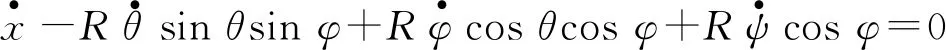
也就是说无穷小运动自由度共有3个.

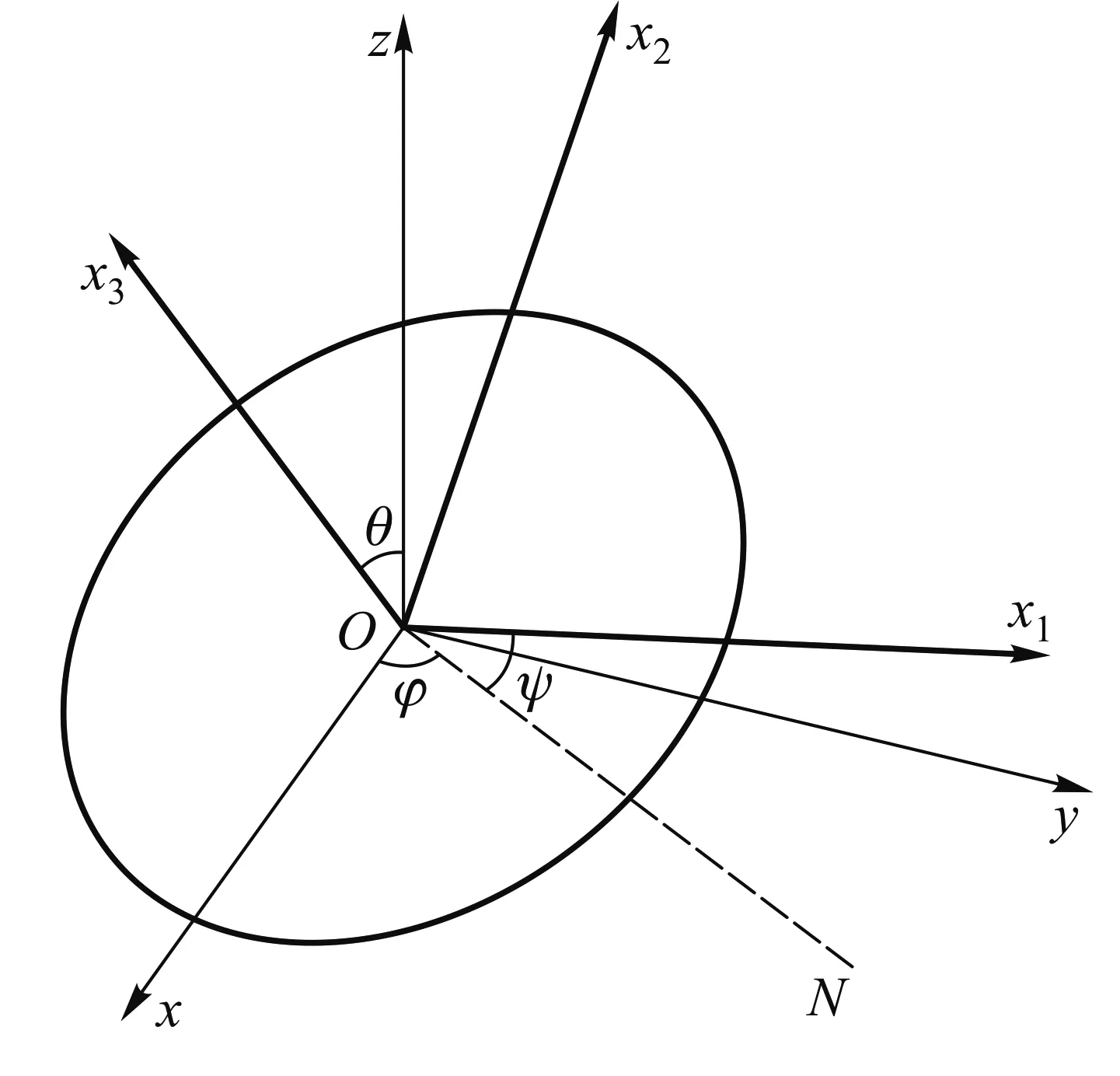
图2 轮的位置

3.2 自行车模型

对于自行车的研究主要是基于用最少的广义坐标描述系统的状态，将完整约束尽可能体现在计算时自由度的减少上. 这样最少需要7个广义坐标(这里模拟时为简单起见并没有将z=Rsinθ两个完整约束直接代换因此使用了9个广义坐标). 而对于动能与势能的表示，需要用这些坐标表示出前后轮的坐标与欧拉角，也就是R.S.Hand在研究自行车系统运动时提到的“auxiliary variables”辅助坐标[2].

图3是一个简化过后的自行车的模型. 后轮的轮心为C1，前轮的轮心为C2. 前轮的转轴在图中以虚线表示，前后轮在同一平面上时(即前轮未转向)转轴与C1C2的交点为C3，夹角为α. 于是C1C3作为X轴与后轮法向量作为Z轴构成车架参考系.

图3 自行车的位形

一个自行车系统具有两个纯滚动的轮，也就是说两个轮在接触处共有6个约束. 而在两轮之间仍有约束，它们都是完整约束. 为了确定自行车的位形，在不考虑纯滚约束的情况下可以使用后轮质心位置C1(x1,y1,z1)，车架的欧拉角θ、φ、ψ，前后轮的自转角ψ1,ψ2，前轮相对于轴转过的角度β共9个广义坐标描述. 参数为轮的半径R，质量m，绕轴转动惯量I，前轮转轴角度α，车架的长度C1C3=d与C3C2=δ.

为求出系统的力学函数与约束，还需要用这9个坐标和完整约束对应的几何关系表示出前后轮坐标与欧拉角共12个坐标. 后轮在笛卡尔坐标系下的位置为

r1=(x1,y1,z1);θ1=θ;φ1=φ;ψ1=ψ1

(5)

而前轮的位置要通过车架参考系变换来求解. 现需要将OXYZ车架参考系绕Z旋转-ψ，再绕X旋转-θ，最后绕Z轴旋转-φ得到Oxyz地面系. 定义旋转矩阵：

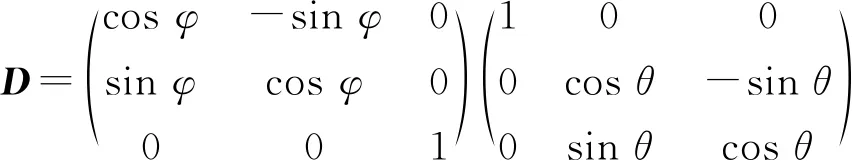
(6)

对应上述旋转，3个矩阵自右向左变换就可以通过乘上矩阵D将OXYZ系中的坐标变换为Oxyz系中的坐标. 而在车架参考系中的前轮中心C2坐标为

(7)

那么前轮在地面参考系中的位矢便为r2=r1+DR2. 前轮法向量n=D(-sinαsinβ,-cosαsinβ,cosβ)，那么欧拉角：

于是我们可以得到两组坐标的变换：

Q=(x1,y1,z1,θ1,φ1,ψ1,x2,y2,z2,θ2,φ2,ψ2)T，

q=(x1,y1,z1,θ,φ,ψ,ψ1,ψ2,β)T

4 模拟结果

在这里我们可以使用第3节中提供的约束矩阵C=C′J与拉格朗日函数：

直接利用非完整约束下的拉格朗日方程近似求解.函数中T1与T2对应前轮与后轮的动能，可用3.1中的动能表达式得到.U为势能函数，即mgz1+mgz2.

而参数我们可以用国际单位制表示现实生活中较为接近的自行车参数. 如下表.

表2 模拟参数(国际单位制)

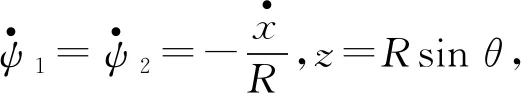
4.1 速度对稳定性的影响

图4是不同初始速度下在满足能量守恒的时间范围内θ与φ随时间的变化. Δt代表近似计算所取的间隔，T为模拟的总时间.θ反映车身的倾角，而φ反映车的转角. 可以看见，速度太小时系统会迅速失去稳定性.

对于可以稳定运行的运动，考虑其坐标变化的总体趋势. 速度大意味着轮的角动量大，也就是说提供同样的力矩情况下，速度大的φ转角变化越慢. 从图中也可以很明显地看出. 定性地来讲，就是角动量越大，越难以改变其运动状态，同时也更加稳定. 考虑一种极限情况，就是速度足够大，相当于重力足够小. 这样的话自行车可以保持其初始状态不变，φ与θ都是恒定值. 这样就可以合理地推测速度越大，θ与φ状态改变地越慢.

图4 θ、φ与t关系图(Δt=0.01 s,T=10 s,δ=0)

4.2 “前轮尾迹”对稳定性的影响

Jones在著作中提及“前轮尾迹”对自行车平衡的重要性. “前轮尾迹”描述转轴-地面交点与前轮接触点的相对位置. 如果转轴交点在车轮交点之前，那么当前轮偏离中央的位置时，地面的摩擦力与车架对前轮的力形成的力矩将与偏转方向相反，反之则相同. 这与脚轮(比如超市中的购物车)的运动具有相似的特征[6]. 现设置不同的δ=C3C2来验证一下“前轮尾迹”对平衡的影响.

由图5可得，转轴与地面的交点位于前轮接触点前的两个运动δ=0,-0.4 m还是相当稳定的，并且距离越大振荡平缓得越快. 而另一个就不是那么稳定了. 不过也并非前轮设置的越靠后越好，由于那样的车过于稳定从而转弯等操作显得并不灵活. 可以看出，模拟结果和Jones在其著作中的论断是一致的，前轮过于靠前是无法骑行的.

图5 θ与t关系图(Δt=0.01 s，T=10 s,v=4 m/s)

4.3 陀螺效应以及前轮的自由度对稳定性的影响

模拟如图6，这两种情况下轮都向一个方向倒下，并且θ的变化情况相同. 这是由于在这两种情况下，都不会由于轮的旋转产生x方向的力矩，θ坐标对应的广义力只由重力产生，最后只能向一个方向倾斜.

再来重点讨论一下陀螺效应的影响. Jones认为陀螺效应的影响是十分小的，但是此处的仿真和简单的推理却显示没有角动量的自行车是无法运行的. 再次回顾Jones的实验，可以发现他是将前轮的角动量抵消，而后轮的角动量仍然是存在的. 于是经过模拟只改变前轮或者后轮某一个轮的动能函数，我们得到如图7的结果.

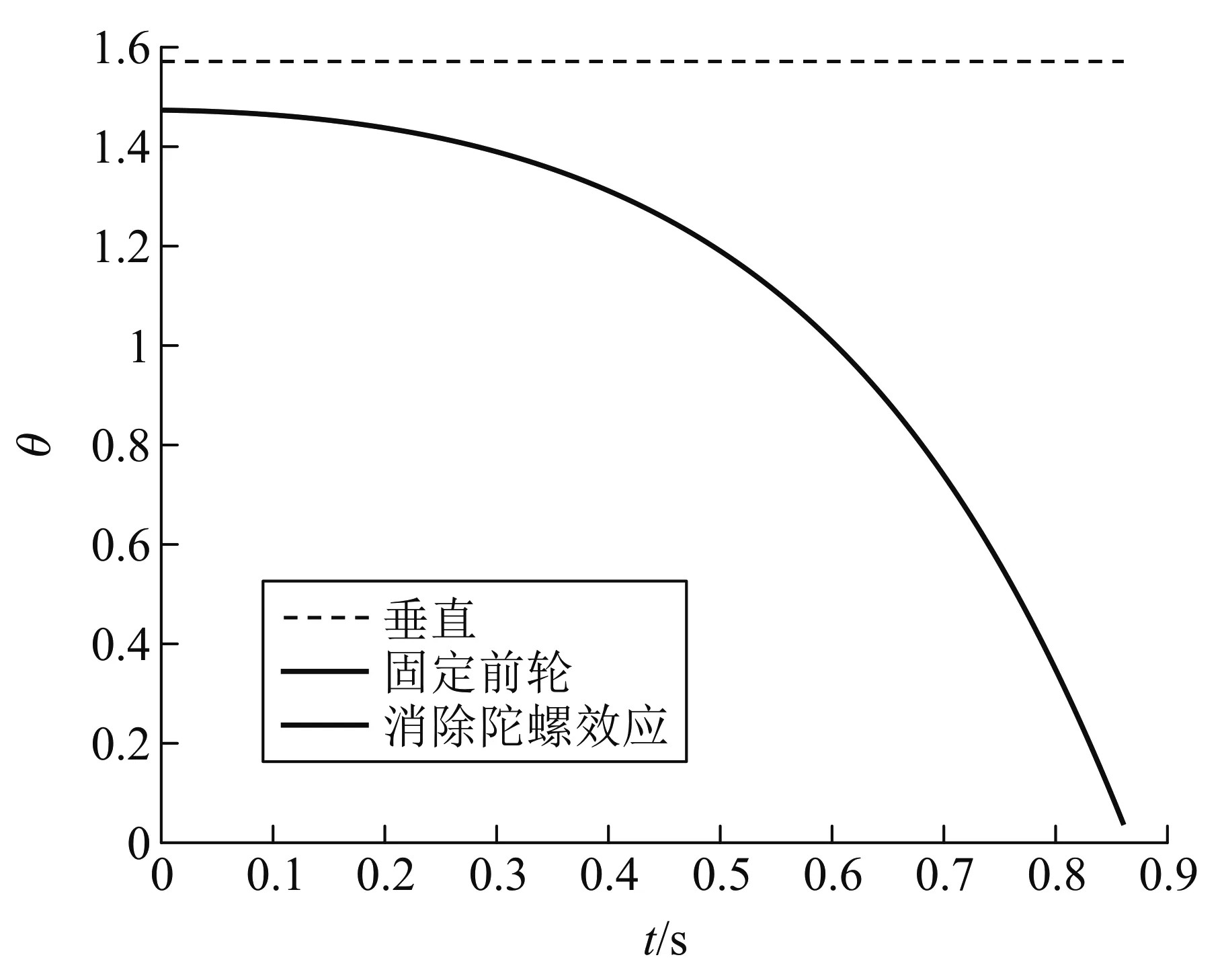
图6 θ与t关系图(Δt=0.01 s，T=0.87 s,v=4 m/s)

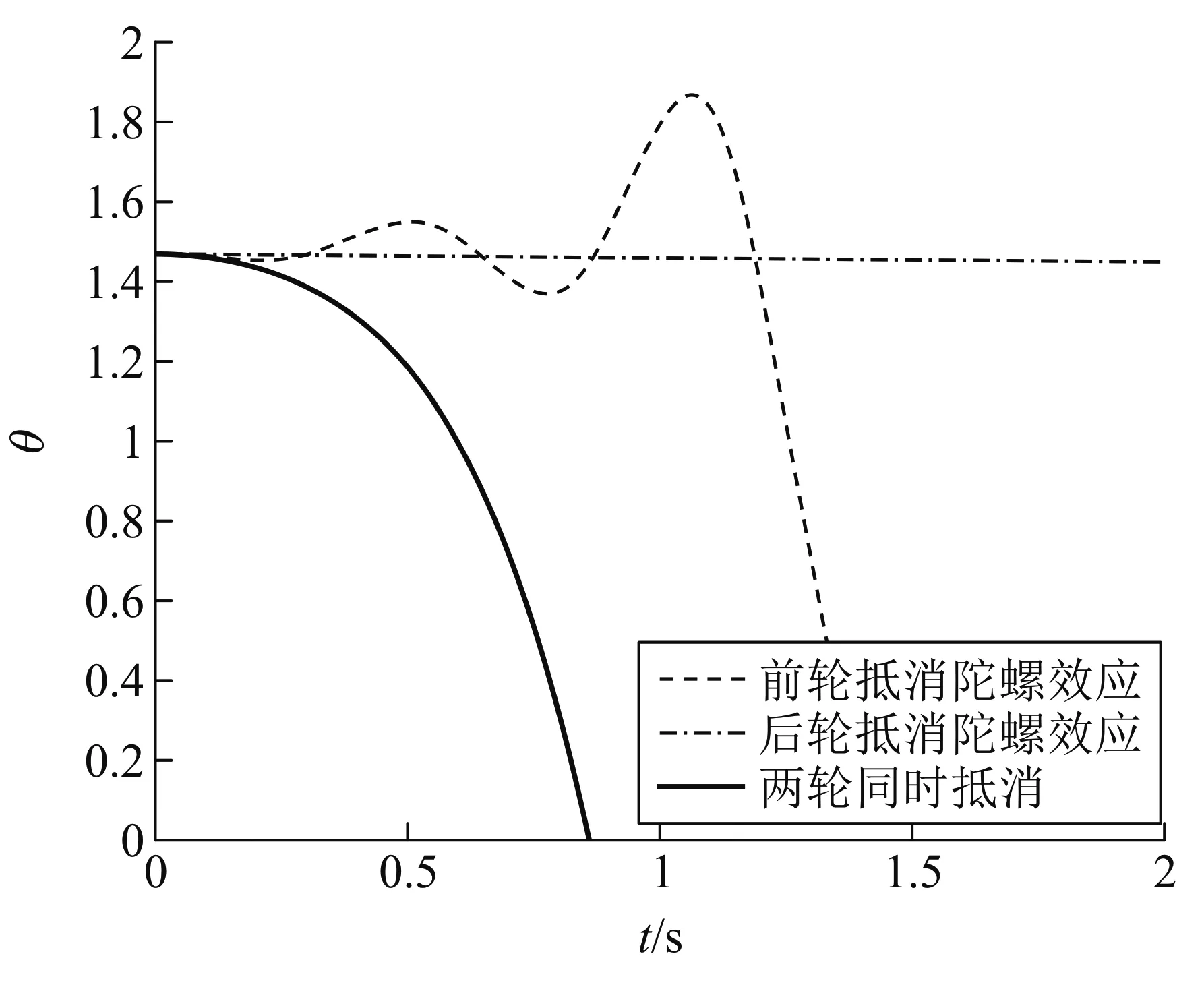
图7 θ与t关系图(Δt=0.01 s，T=0.87 s,v=16 m/s)

Jones制作的自行车“URB I”[3]即图中虚线所代表的只抵消前轮角动量的情况，也并不是完全不稳定的. 加之其实验中并没有完全使轴对齐且平面重合，并不能说是完全抵消，人还是可以操控这样的自行车的. 不过显然这样会比普通的车更加地难以操控，Jones也提到这样的自行车无法在没有人的操控下稳定运行. 从图中也可以清晰地看见，当后轮的陀螺效应被消除后，自行车仍能在前轮角动量的调节下保持相当稳定. 也就是说前轮对于稳定性的贡献是远远大于后轮的.

以上模拟了自行车自由运动下的一个简单模型，而在实际情况下，由于骑行者操控反馈的存在，这个系统成为一个非封闭的系统，情况变得更加复杂. 不过自行车自由和被操控时运动的稳定性一定是紧密联系的. 因此分析力学的方法可以在近似计算自行车这样自由度较高的系统上有着比较简洁的应用.