关于三能级系统微扰矩阵元对能量修正的影响
秦志杰,李德民
(郑州大学 物理工程学院,河南 郑州 450001)
微扰论是量子力学一种重要的近似方法[1,2]。采用微扰论求解时,要求体系哈密顿可以分为两部分,一部分是未微扰部分,另一部分是微扰部分,并且还要求未微扰部分可严格求解,微扰部分相对于可严格求解部分很小才行。微扰法从未受微扰体系的解出发,通过求解引入微扰后体系的能级和状态的变化,算出对能级和波函数的各阶修正。
在教学过程中,我们发现学生对于微扰计算方法的解题过程很熟悉,但对于计算出的结果和微扰的直接联系却不太清楚。比如,给出微扰,学生能计算出各阶修正,但是对下述问题并不太清楚。即,微扰矩阵元的位置和大小对能量的各阶修正的具体联系是什么?能否仅通过观察微扰矩阵的形式,就看出对各能级的各阶能量修正是否存在?以及相应修正是提升还是降低了原有能级的能量?对这些问题的回答,一方面可以加深对微扰论的理解;另一方面,也能对微扰矩阵元的影响有更深的认识。实际上,很多可用微扰论处理的问题,不经计算即可对结果做出判断。
为了解决上述问题,我们将通过对具体系统的计算和分析,来寻找微扰矩阵元和微扰论方法计算结果之间存在的联系。接下来,通过对存在微扰的三能级系统的研究,来寻找微扰矩阵元和对各能级的不同阶修正之间可能存在的联系。
1 含微扰的三能级系统的描述
我们首先考虑一个存在微扰的三能级系统,体系总的哈密顿可写为:
(1)
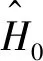

(2)
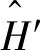
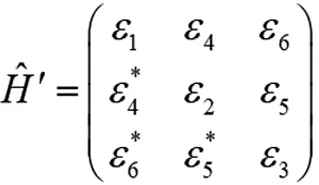
(3)
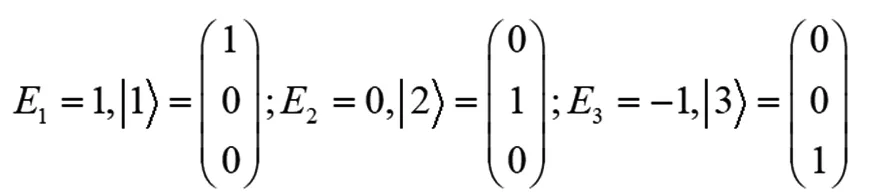
(4)
2 微扰论对能级的修正
2.1 微扰矩阵对能级的一阶修正
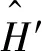
(5)
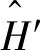
因此,对E1能级的一阶修正为:
(6)
对E2能级的一阶修正为:
(7)
对E3能级的一阶修正为:
(8)
上述结果显示,只有微扰矩阵的对角元,才会对相应的能级产生一阶修正;而微扰的非对角元不会对能级产生一阶修正。我们这里讨论的是不含微扰时,体系由对角化矩阵描述的系统。对于零阶矩阵非对角化的情况,要首先把非微扰部分化为对角形式后,才能按上述结果进行讨论。
2.2 微扰矩阵对能级的二阶修正
(9)
从上述结论可知,对于有限个能级组成的系统,就微扰矩阵的非对角元对于能量最低的能级Emin的修正而言,由于其余所有能级均大于这个能量,所以上述修正始终小于或等于零,即,对最低能级的二阶修正不会大于零。换句话说,微扰矩阵的非对角元的二阶修正,只会拉低能级Emin。同理,对于能量最高的能级Emax的修正,由于其余所有能级均小于这个能量,所以上述修正始终大于或等于零,即,对微扰矩阵的任意非对角元,它对最高能级的二阶修正不会小于零。换句话说,微扰的二阶修正,只可能提升最高的能级Emax。
利用上述公式,对能量为E1的能级的二阶修正为:
(10)
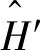
(11)
上述二阶修正项均大于等于零,这一点与前面的分析一致。即,由于E1为能量最高的能级,有前面结论可知,所有二阶修正均为正。
同理,对能量为E2的能级的二阶修正为:
=-|ε4|2+|ε5|2
(12)
对能量为E3的能级的二阶修正为:
(13)
上式关于能量的二阶修正均小于等于零,这一点与前面的结论一致。即,由于E3为能量最低的能级,由前面结论可知,所有二阶修正均为负。
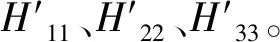

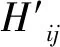
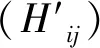
此外,考虑到用微扰论进行实际计算时,往往只需要计算出微扰所产生的低阶修正,因此我们仅研究到二阶近似,不再考虑更高阶的能量修正。
3 结论
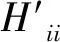
利用上述结论,对于存在微扰的体系,我们可以很快判断出,微扰矩阵会对哪些能级带来什么样的修正。并在计算前,可以判断出修正的作用效果,从而减少计算量。同时,这些结论还可为通过微扰的引入来控制体系能谱提供一定的帮助,从而更好的把握如何通过微扰项来控制能级的位置,提高对量子体系的调控能力。

