两自由度微扰力学系统的二阶近似守恒量*
楼智美
(绍兴文理学院物理系,绍兴 312000)
引言
为研究方便,在建立力学系统模型时常常会忽略一些次要因素或把某些条件理想化,使建立的力学系统与实际的力学系统存在一定的差异,从而导致其研究成果不能直接应用于实际的力学系统.若重新考虑在建立力学模型时忽略的某些次要因素或考虑某些实际的条件,则描述力学系统的运动微分方程中就会出现微扰项,存在微扰项的力学系统叫微扰力学系统.微扰力学系统更接近实际的力学系统,其研究成果更适合推广应用.微扰力学系统近似守恒量的研究对于研究力学系统的特性至关重要.近年来关于微分方程近似守恒量的研究已取得不少成果[1-15],目前研究近似守恒量主要采用近似Lie对称性理论[1]和近似 Noether对称性理论[2],引进近似的群无限小变换,微分方程在此变换下近似保持不变则为近似Lie对称性;哈密顿作用量在此变换下近似保持不变则为近似Noether对称性,所得的守恒量为近似守恒量.用近似对称性理论求近似守恒量要用到Lagrange函数和近似的群无限小变换,并需解出近似的无限小生成元、规范函数,计算较繁复,尤其对计算多自由度二阶及以上阶近似守恒量带来了困难.另外,用近似对称性理论求近似守恒量时,无法明确表达高阶近似守恒量与低阶近似守恒量、一阶近似守恒量与精确守恒量间的递推关系,给理论的推广应用带来了不便.
本文研究微扰力学系统的二阶近似守恒量,把微扰力学系统视为未受微扰系统与微扰项的迭加,先选择合适的方法求得未受微扰系统的精确守恒量I0[16,17],再从近似守恒量的性质出发,得到守恒量的一阶微扰项系数I1与精确守恒量I0、守恒量的二阶微扰项系数I2与守恒量的一阶微扰项系数I1和精确守恒量I0的递推关系,并考虑微扰项对精确守恒量以及对守恒量的一阶微扰项系数的影响,利用递推关系并直接积分求得二阶近似守恒量.文中用此方法研究了一微扰力学系统的二阶近似守恒量并得到了2个稳定的二阶近似守恒量.
1 求两自由度微扰力学系统二阶近似守恒量的基本理论
两自由度微扰力学系统的运动微分方程一般可表示成
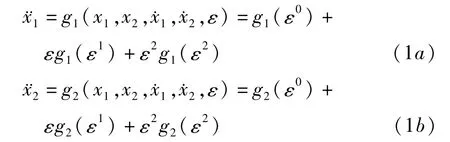
其中 0<ε≪1,g1(x1,x2,˙x1,˙x2,ε),g2(x1,x2,˙x1,˙x2,ε)为广义加速度,可表示成未受微扰作用时的广义加速度 g1(ε0),g2(ε0)和因微扰作用产生的一阶微扰项 εg1(ε1)、εg2(ε1)及二阶微扰项 ε2g1(ε2)、ε2g2(ε2)之和,g1(ε1),g2(ε1),g1(ε2),g2(ε2)分别表示一阶、二阶微扰项的系数(下文表示类同).与系统(1)相应的未受微扰作用系统的运动微分方程可表示成
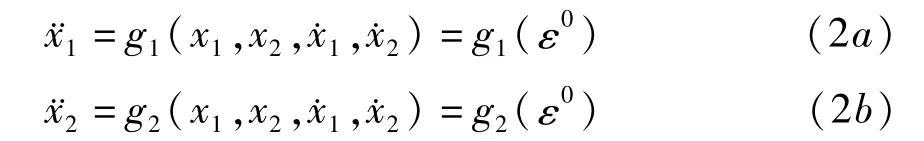
系统(1)可视为系统(2)与一阶微扰项 εg1(ε1)、εg2(ε1)及二阶微扰项 ε2g1(ε2)、ε2g2(ε2)的迭加.
二阶近似守恒量可表示成

式(3)中的I1、I2分别称为守恒量的一阶微扰项系数和二阶微扰项系数,若I0不为0,I1、I2均为0,则称 I=I0为精确守恒量;若 I0、I1不为 0,I2为 0,则称I为稳定的一阶近似守恒量;若I0、I2不为0,则称I为稳定的二阶近似守恒量;若I0、I2为0,I1不为0,则称I为平凡的一阶近似守恒量;若I0为0,I2不为0,则称I为平凡的二阶近似守恒量.
二阶近似守恒量的性质为

将(3)式代入(4)式并展开,令 ε0,ε1,ε2的系数分别等于0,忽略ε3及以上项,可得守恒量的一阶微扰项系数I1与精确守恒量I0,二阶微扰项系数I2与一阶微扰项系数I1及精确守恒量I0的递推关系
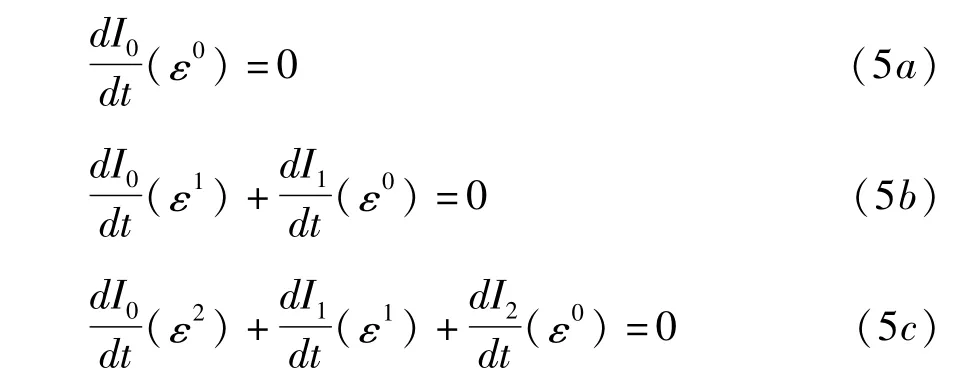
从系统(2)求得的精确守恒量I0一定满足(5a)式,将代入(5b)式可得,同时考虑 g1(ε0),g2(ε0)的形式可求得 I1.由 I1及 εg1(ε1)、εg2(ε1)可求得代入(5c)式,并同时考虑 g1(ε0),g2(ε0)的形式可求得I2.
综上所述,二阶近似守恒量(3)中的第一部分I0的形式是由未受微扰系统(2)决定的,而守恒量的一阶微扰项系数I1的形式是由未受微扰系统和一阶微扰项 εg1(ε1)、εg2(ε1)共同决定的,一阶微扰项 εg1(ε1)、εg2(ε1)对精确守恒量 I0产生影响,此影响体现在中,而由确定 I1时又要考虑未受微扰项 g1(ε0),g2(ε0)的形式,从而实现 g1(ε0),g2(ε0)项对 I1的影响.类似地,守恒量的二阶微扰项系数I2的形式是由未受微扰系统和微扰项 εg1(ε1)、εg2(ε1)、ε2g1(ε2)、ε2g2(ε2)共同决定的,二阶微扰项 ε2g1(ε2)、ε2g2(ε2)会对(ε2)产生影响,一阶微扰项 εg1(ε1)、εg2(ε1)会对产生影响,而由确定 I2时又要考虑未受微扰项 g1(ε0),g2(ε0)的形式,实现 g1(ε0)、g2(ε0)项对 I2的影响.
因此,求系统(1)的二阶近似守恒量的步骤可归结如下:首先,分解微扰力学系统并求得精确守恒量,即将系统(1)分解成未受微扰系统(2)和微扰项,并根据系统(2)的形式选择一种合适的方法求得其精确守恒量I0,由此求得的守恒量中不含微扰项.其次,建立守恒量的高阶微扰项系数与低阶微扰项系数及精确守恒量之间的递推关系,即根据二阶近似守恒量的性质,建立守恒量的一阶微扰项系数I1与精确守恒量I0、二阶微扰项系数I2与一阶微扰项系数I1和精确守恒量I0的递推关系.第三,考虑微扰项的影响,利用递推关系直接积分求得守恒量的一阶、二阶微扰项系数,即考虑微扰项εg1(ε1)、εg2(ε1)、ε2g1(ε2)、ε2g2(ε2)对精确守恒量I0的影响,计算代入(5b)式并同时考虑 g1(ε0)、g2(ε0)的形式求得I1;考虑微扰项 εg1(ε1)、εg2(ε1)对守恒量的一阶微扰项系数I1的影响,计算,将和代入(5c)式并同时考虑 g1(ε0)、g2(ε0)的形式求得I2.
2 应用举例
设两自由度微扰力学系统的运动微分方程可表示成
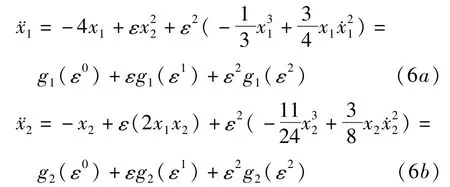
其中ε为非线性耦合系数,且0<ε≪1.与系统(6)相应的未受微扰系统为

系统(7)是频率比为2:1的两维各向异性谐振子,存在如下4个精确守恒量[18]

下面计算.将(8)式分别代入,并同时考虑(6)式得
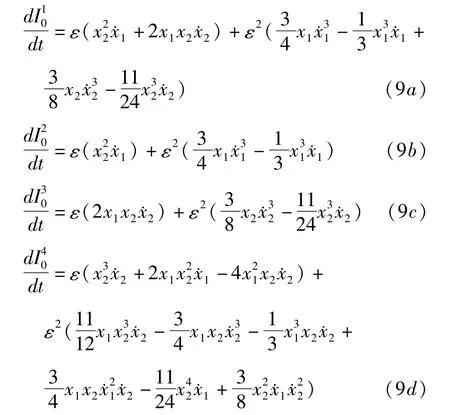
将(9)式中的项分别代入(5b)式,并同时考虑(6)式中 g1(ε0),g1(ε0)项的形式,可求得与相对应的2个I1
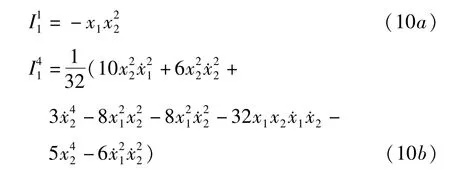
与相应的I1不存在.
下面计算,将(10)式分别代入并考虑(6)式中 εg1(ε1),εg1(ε1)项的形式,得
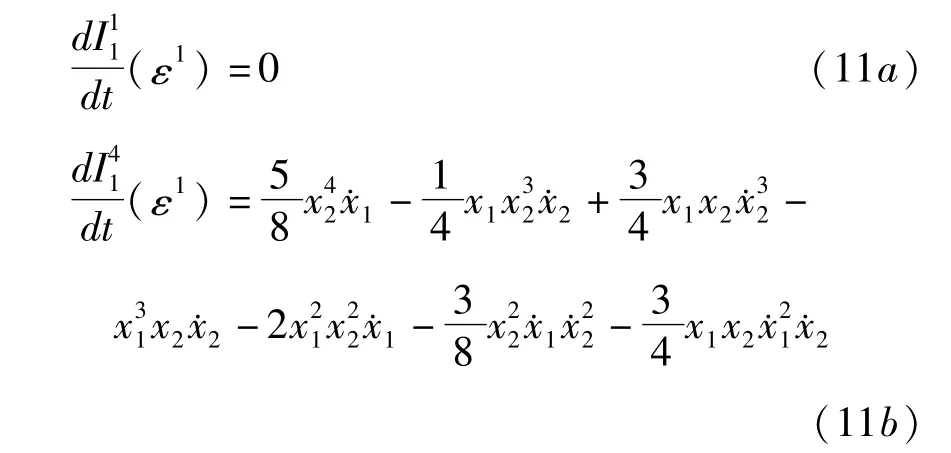
将(9a)式中的项和(11a)式代入(5c)式,并考虑(6)式中 g1(ε0),g1(ε0)项的形式,可得

将(9d)式中的项和(11b)式代入(5c)式,并考虑(6)式中 g1(ε0),g1(ε0)项的形式,可得

因此,系统存在2个稳定的二阶近似守恒量
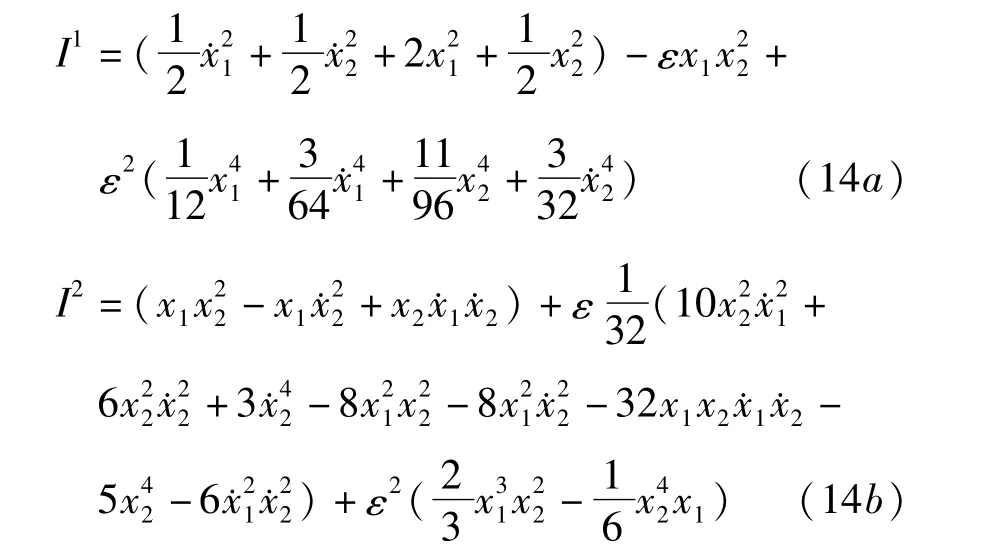
另外,由于精确守恒量的必为 0,则系统一定存在以下4个平凡的二阶近似守恒量

其中的由(8)式给出.
3 小结
本文从二阶近似守恒量的性质出发研究微扰力学系统的二阶近似守恒量,提出了分三步求得二阶近似守恒量的直接积分法:首先,分解微扰力学系统并求得精确守恒量;其次,建立守恒量的高阶微扰项系数与低阶微扰项系数及精确守恒量之间的递推关系;第三,考虑微扰项的影响,利用递推关系直接积分求得守恒量的一阶、二阶微扰项系数,从而求得系统的二阶近似守恒量.文中用此方法研究了一微扰力学系统的二阶近似守恒量并得到了2个稳定的二阶近似守恒量和4个平凡的二阶近似守恒量.用本方法求近似守恒量,思想方法简单,高阶近似守恒量与低阶近似守恒量间的递推关系明确,可推广至多自由度微扰力学系统及高阶近似守恒量的求解,是求近似守恒量的一种有效方法.
1 Leach PG L,Moyo S,Cotsakis S,Lemmer R L.Symmetry,singularities and integrability in complex dynamicsⅢ:approximate symmetries and invariants.Journal of Nonlinear Mathematical Physics,2001,8(1):139~156
2 Govinder K S,Heil T G,Uzer T.Approximate Noether symmetries.Physics Letters A,1998,240(3):127~131
3 Unal G.Approximate generalized symmetries,normal forms and approximate first integrals.Physics Letters A,2000,266(2):106~122
4 Kara A H,Mahomed FM,Unal G.Approximate symmetries and conservation laws with application.International Journal of Theoretical Physics,1999,38(9):2389~2399
5 Johnpillai A G,Kara A,H.Variational formulation of approximate symmetries and conservation laws.International Journal of Theoretical Physics,2001,40(8),1501~1509
6 Dolapci I T,Pakdemirli M.Approximate symmetries of creeping flow equations of a second grade fluid.International Journal of Non-linear Mechanics,2004,39(10):1603~1619
7 Kara A H,Mahomed FM,Qadir A.Approximate symmetries and conservation laws of the geodesic equations for the Schwarzschild metric.Nonlinear Dynamics,2008,51(1-2):183~188
8 Grebenev V N,Oberlack M.Approximate Lie symmetries of the Navier-Stokes equations.Journal of Nonlinear Mathematical Physics,2007,14(2):157~163
9 Johnpillai A G,Kara A H,Mahomed F M.Approximate Noether-type symmetries and conservation laws via partial Lagrangians for PDEs with a small parameter.Journal of Computational and Applied Mathematics,2009,223(1):508~518
10 楼智美.微扰Kepler系统轨道微分方程的近似Lie对称性与近似不变量.物理学报,2010,59(10):6764~6769(Lou ZM.Approximate Lie symmetries and approximate invariants of the orbit differential equation for perturbed Kepler system.Acta Physica Sinica,2010,59(10):6764~6769(in Chinese))
11 Naeem I,Mahomed FM.Approximate first integrals for a system of two coupled van der Pol oscillators with linear diffusive coupling.Mathematical and Computational Applications,2010,15(4):720~731
12 楼智美,梅凤翔,陈子栋.弱非线性耦合二维各向异性谐振子的一阶近似Lie对称性与近似守恒量.物理学报,2012,61(11),110204(Lou Z M,Mei F X,Chen Z D.The first-order approximate Lie symmetries and approximate conserved quantities of the weak nonlinear coupled two-dimensional anisotropic harmonic oscillator.Acta Physica Sinica,2012,61(11):110204(in Chinese))
13 Zhang Z Y,Yong X L,Chen Y F.A new method to obtain approximate symmetry of nonlinear evolution equation form perturbations.Chinese Physics B,2009,18(7):2629~2633
14 楼智美.两自由度弱非线性耦合系统的一阶近似Lie对称性与近似守恒量.物理学报,2013,62(22):220202(Lou ZM.The first order approximate Lie symmetries and approximate conserved quantities of the weak nonlinear coupled two-dimensional system.Acta Physica Sinica,2013,62(22):220202(in Chinese))
15 楼智美.含非线性微扰项的二阶动力学系统的一阶近似守恒量的一种新求法.物理学报,2014,63(6):060202(Lou ZM.A new method to obtain first order approximate conserved quantities of second-ordinary dynamics system containing nonlinear perturbation terms.Acta Physica Sinica,2014,63(6):060202(in Chinese))
16 张斌,方建会,张东爱,徐瑞莉,刘学锋.相对论性非完整系统的Lagrange对称性与守恒量.动力学与控制学报,2014,12(2):105~110(Zhang B,Fang JH,Zhang D A,Xu R L,Liu X F.Symmetry and conserved quantity of Lagrangians for relativistic nonholonomic system.Journal of Dynamicsand Control,2014,12(2):105~110(in Chinese))
17 徐瑞莉,方建会,张斌,王菲菲.Chetaev型非完整系统Nielsen方程Lie对称性导致的一种守恒量.动力学与控制学报,2014,12(1):13~17(Xu R L,Fang JH,Zhang B,Wang F F.A type of conserved quantity of lie symmetry for nonholonomic system of nielsen equation of chetaev's type.Journalof Dynamicsand Control,2014,12(1):13~17(in Chinese))
18 楼智美,梅凤翔.二维各向异性谐振子的第三个独立守恒量及其对称性.物理学报.2012,61(11):110201(Lou Z M,Mei F X.The third independent conserved quantity and its symmetry of the two-dimensional anisotropic harmonic oscillator.Acta Physica Sinica,2012,61(11):110201(in Chinese) )

