蔡氏混沌电路频谱分布与元件参数的选择*

韩敬伟 王忠林

（1.滨州学院物理与电子科学系，滨州 256603）（2.南开大学计算机与控制工程学院，天津 300071）

引言

华裔物理学家蔡少棠（Leon O.Chua）教授于1983年提出并实现蔡氏混沌电路［1］，促进了非线性电路理论的发展，在掀起了研究非线性电路的热潮，为混沌从理论走向实际奠定了基础.蔡氏混沌电路具有丰富的混沌动力学特性，并且易于实现，因此受到了广泛的关注和研究.近几年，利用不同模型忆阻器代替蔡氏二极管构成蔡氏忆阻混沌电路获得了大量的研究［2－8］.

把混沌应用于保密通信中是在1989年提出，因为混沌信号具有无限状态模式、宽频带特性和不可预测性，比伪随机序列更适合应用于保密通信领域，因此在国际上获得了广泛的重视与研究［9－13］.但在实际通信系统中，通信信道的带宽有一定限制.超过信道频谱范围的频率分量将要被滤掉，这样就给混沌实际电路用于保密通信带来困难，因此有关混沌系统的频率特性也获得了部分研究者的注意［14－15］.由于混沌信号具有无限状态模式，所以混沌系统处于混沌状态时其频谱必定是连续谱，否则其频谱为分立谱.因此，频谱分析也被做为判断系统是否处于混沌状态的一个重要依据［16－20］.文献14给出了蔡氏电路一个估计其频谱分布范围的简单公式，并从该公式和蔡氏电路α-β分叉曲线出发设计了一个输出信号基本满足预先指定的频谱分布范围的蔡氏电路.文献15以蔡氏混沌电路为例，通过对蔡氏混沌电路中元器件R、L和C参数的调整，可以获得具有期望频谱范围的混沌信号.文献14、15都只是对蔡氏电路进行了MATLAB软件仿真，没有进行电路仿真，而且只讨论了一种电路参数改变方法.

本文以蔡氏电路为研究对象，根据其归一化方程中各参数的表达式，分别研究了三改变元件参数，但仍然保持混沌归一化方程不变的途径，并利用multsim软件对三种情况进行了电路仿真，获得了不同参数情况下混沌电路的频谱图像和频率范围，结果和理论分析一致.这将有助于加深人们对蔡氏混沌电路的频率特性认识，方便电路设计工程师据此选择不同元件参数设计和实现具有期望频率范围的混沌电路.

1 理论分析

典型蔡氏混沌系统的Multisim仿真电路（如图1）所对应的电路方程为：

图1 典型蔡氏混沌Multisim仿真电路图Fig.1 Multisim simulation circuit of canonical Chua′s chaotic system

其中a、b、E是蔡氏二极管（蔡氏二极管由电阻和集成运放来实现）的分段线性斜率和转折电压，分别表示为：

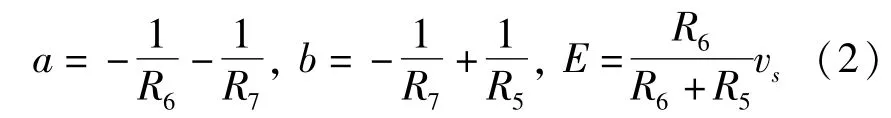
其中vs为运放饱和电压.

对公式（1）进行电路归一化分析，做如下变量代换：

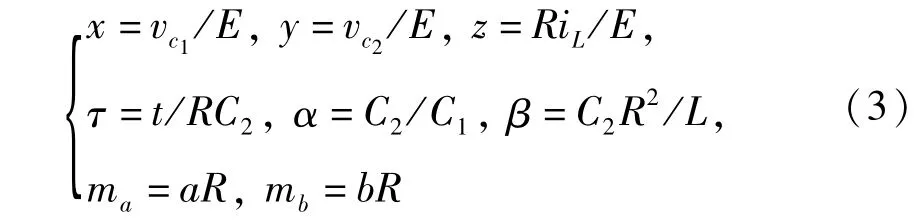
其中R称为归一化电阻，C2称为归一化电容.时间变换因子τ是实际时间t与归一化时间RC2的比值，在分析中做为混沌系统频率范围测算的一个重要依据.RC2越小，τ越大，混沌系统频率范围越大；RC2越大，τ越小，混沌系统频率范围越小，这在后面的仿真分析中可以明显的看到.

把（3）式代入（1）式后，整理为如下无量纲表达式：

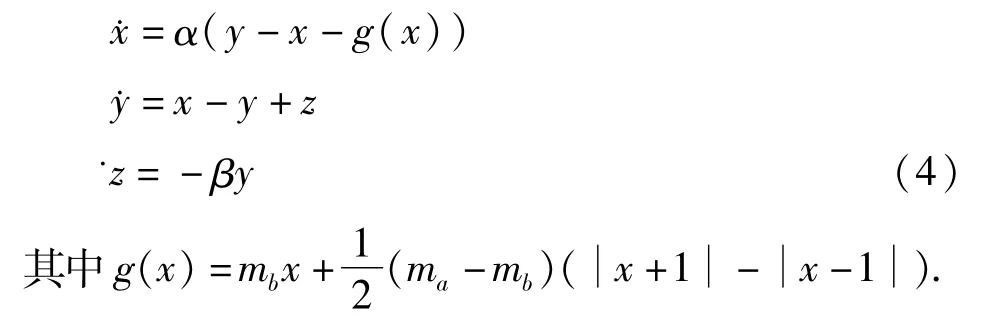
结合（2）、（3）、（4）式来看，在改变电路元件参数时，只要保持混沌电路归一化方程（4）式不变，理论上就可以保证改变参数后的电路依然处于混沌状态.电路元件参数的改变可以分为三种情况.

1.1 一种动态元件改变

一种动态元件和所有的电阻同步改变，另一种动态元件保持不变.例如：所有电阻均增大m倍，电容减小为原来，代入（2）、（3）式，有：

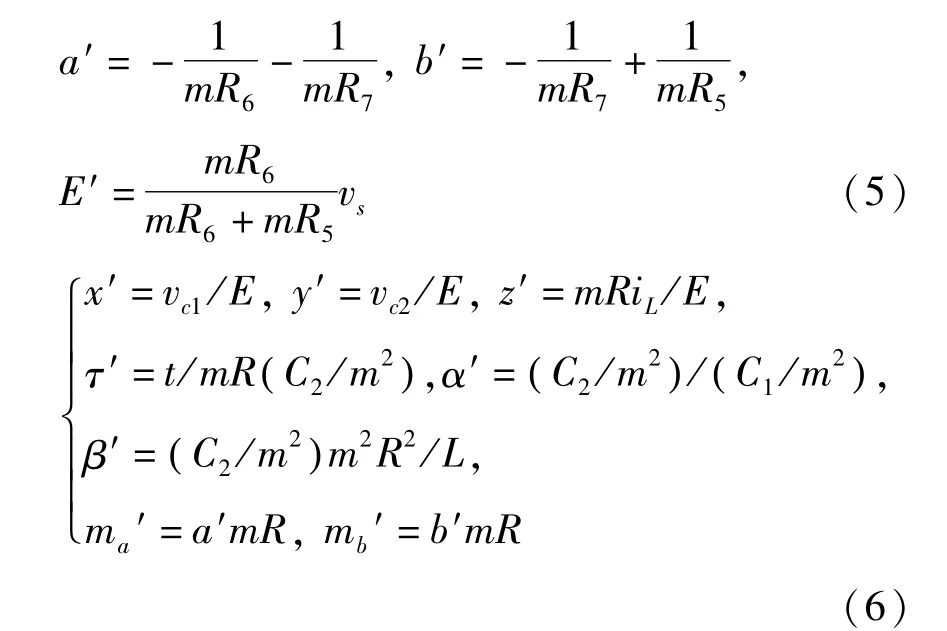
比较（2）、（5）和（3）、（6）式，发现 a′、b′虽然发生了变化，但 ma′、mb′和 E′保持不变，即蔡氏二极管的归一化特性方程没有变化.（6）式中 α′、β′与（3）式中α、β一致，没有发生变化，即归一化方程（4）没有变化；但时间变换因子变为 τ′＝mτ，比原先增大了m倍，即在该情况下混沌系统的频率范围应增大为原来的m倍.

1.2 两种动态元件改变

如果保持所有电阻保持不变，而同时同向改变动态元件参数（文献8）时.例如电感和电容均增大m倍，因电阻不变，所以（2）式中各个量保持不变，只看（3）式即可.因此，把改变后的值代入（3）式，有：

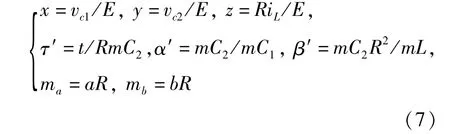
比较（3）、（7）两式发现只有时间变换因子变为 τ′＝t/RmC2＝τ/m，即时间变换因子减小为原来的，很明显时间变换因子与电容C2的变化相反.因为其他参数未发生变化，所以归一化方程（4）没有改变，该情况下电路系统仍为混沌状态，但其频率范围应缩小为原来的.

1.3 三种元件都改变

电感和所有电阻变化相同，电容变化趋势与之相反.如电感和所有电阻都增大为原来的m倍，电容减小为原来的，各元件变化情况代入（2）、（3）式，有：

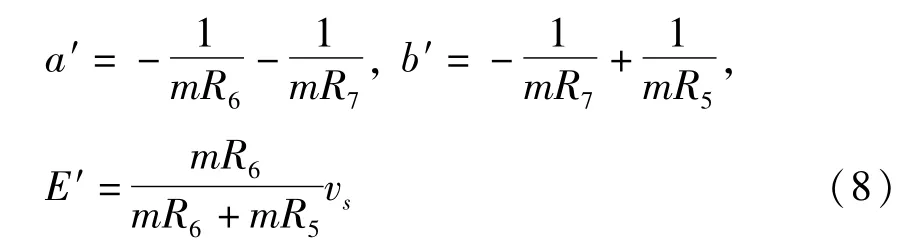
比较（2）、（8）和（3）、（9），可以发现除去 a′、b′发生变化外，其余参数值均没有发生任何变化，所以电路的归一化方程（4）不会改变.因此，该情况下电路依然为混沌状态，且电路频谱和频率范围也应该不会发生任何变化.

2 Multisim电路仿真及分析

NIMultisim软件结合了直观的捕捉和功能强大的仿真，能够快速、轻松、高效地对电路进行设计和验证，一个专门用于电子电路仿真与设计的EDA工具软件，所以常被研究者用来设计混沌系统电路［19－21］.为了验证以上理论分析结果，下面利用Multisim对上述三种情况进行了电路仿真，给出元件改变前后各电路变量的频谱图像，并根据仿真图像进行了进一步的分析.以下分析均在图1所采用的典型参数基础上进行元件参数的调整.

2.1 一种动态元件改变时的仿真分析

在图1所示电路基础上，使电容减小4倍，电阻增大2倍，电感保持不变时，即电路元件参数变为：L＝17mH，C2＝25nF，C1＝2.5nF，R＝3kΩ，有源二极管参数：R2＝R3＝440Ω，R7＝4.4kΩ，R4＝R5＝44kΩ，R6＝6.6kΩ.典型参数下的Multsim仿真结果如图2所示，改变后的如图3所示.

对比图2与图3可以发现，当电容减小4倍，电阻增大2倍，电感保持不变时，电路系统依然保持混沌状态.从各对应电路变量频谱图像形态来看，改变前后几乎一致；从频率范围来看，电容减小4倍后频谱范围扩大约2倍.即蔡氏混沌电路中电容减小a2倍、电阻增大a倍，电感保持数不变时，系统仍然能呈现混沌状态，但频率范围随电容的减小而增大.同样的情况也发生在电容保持不变，电感和电阻改变时.从仿真结果来看，与前面该情况下的理论分析结果一致，即蔡氏混沌电路可以通过调整一个动态元件来改变混沌系统的频率范围.

需要注意的是这种改变是在一定参数范围内能保持其混沌行为不变，一旦超出这个参数空间，混沌系统的行为会发生改变.根据仿真结果来看，在电容C减小100倍、电阻增大10倍时，混沌系统相图由典型的双涡卷开始向单涡卷转变，混沌系统的动力学行为不再保持不变，如图4所示.即在该情况下，电容减小100倍、电阻增大10倍是保持其混沌行为不变的极限.

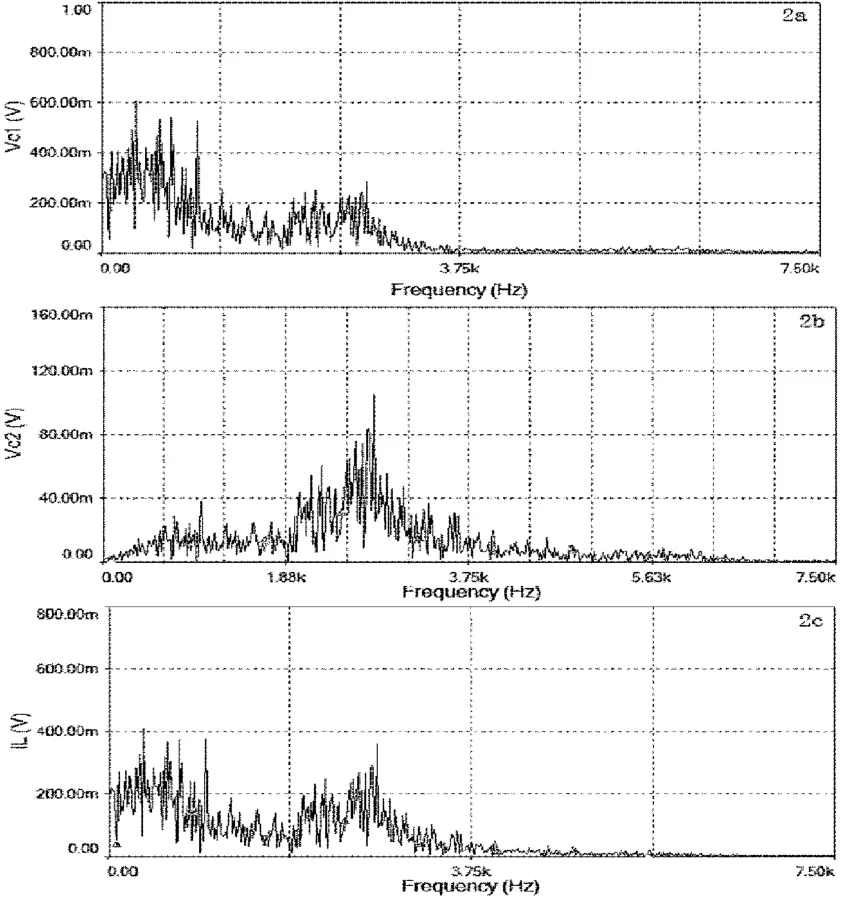
图2 信号频谱图：（a）C1电压信号，（b）C2电压信号，（c）L电流信号Fig.2 Signal spectrum：（a）Voltage signal of capacitor C1（b）Voltage signal of capacitor C2（c）Current signal of inductor L

图3 信号频谱图：（a）C1电压信号，（b）C2电压信号，（c）L电流信号Fig.3 Signal spectrum：（a）Voltage signal of capacitor C1（b）Voltage signal of capacitor C2（c）Current signal of inductor L L

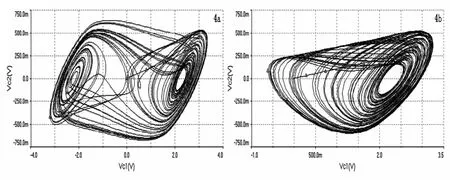
图4 混沌系统Vc1、Vc2相图：（a）典型参数，（b）电容减小100倍，电阻增大10倍Fig.4 Vc1 and Vc2 phase portraits of chaotic system＇s：（a）With typical parameters（b）With capacitance decrease 100 times and resistance increases 10 times

2.2 两种动态元件改变的情况

在文献8中讨论了当同时增大或减小电路中的电容、电感，而保持电阻不变时的情况，在一定参数空间内系统依然呈现混沌状态.这里也进行了multsim仿真实验，其结果如图5所示，其改变后的电路元件参数变为：L＝170mH，C2＝1000nF＝1uF，C1＝100nF＝0.1uF.multsim仿真发现，该参数情况下，系统仍然呈现混沌状态，其各电路信号的频谱分布如图5所示.

图5 信号频谱图：（a）C1电压信号，（b）C2电压信号，（c）L电流信号Fig.5 Signal spectrum：（a）Voltage signal of capacitor C1（b）Voltage signal of capacitor C2（c）Current signal of inductor L

对比图2和图5发现，当电容和电感均增大a倍，频率范围减小a倍，即频率范围随动态元件的增大而减小，反之亦然.

在仿真时同样发现，当参数变化超出合理的参数空间时，系统的混沌动力学特性也会发生变化.当电容、电感均减小10倍时，系统也变成了单涡卷，图6是该情况时的频谱图像.很明显该情况下电容C1电压和电感电流iL的频谱中只有一个非常突出的频率尖峰，表明系统变为单涡卷混沌系统.即该情况下，电容、电感均减小10倍是保持其混沌行为不变的极限.

2.3 三种元件同时改变

当电阻、电感减小10倍，电容增大10倍时，即电路元件参数调整为：L＝1.7mH，C2＝1uF，C1＝0.1uF，R＝150Ω，有源二极管参数：R2＝R3＝22Ω，R7＝220Ω，R4＝R5＝2.2kΩ，R6＝330Ω.multsim仿真发现，该参数情况下，系统仍然呈现混沌状态，其各电路信号的频谱分布如图7所示.

图6 信号频谱图：（a）C1电压信号，（b）C2电压信号，（c）L电流信号Fig.6 Signal spectrum：（a）Voltage signal of capacitor C1（b）Voltage signal of capacitor C2（c）Current signal of inductor L

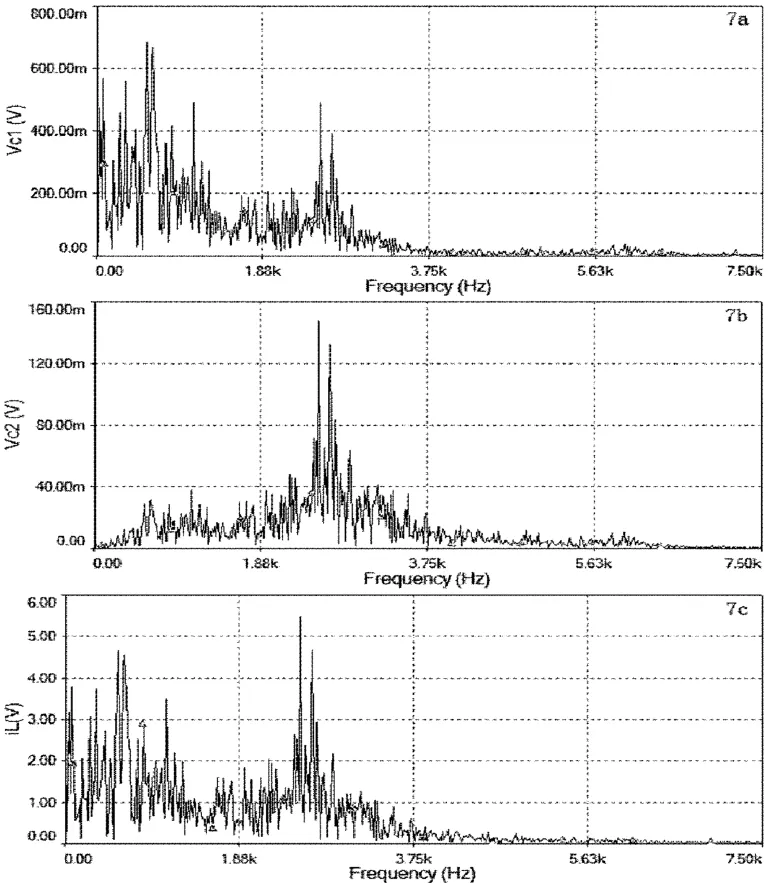
图7 信号频谱图：（a）C1电压信号，（b）C2电压信号，（c）电流信号Fig.7 Signal spectrum：（a）Voltage signal of capacitor C1（b）Voltage signal of capacitor C2（c）Current signal of inductor L

对比图2和图7发现，元件参数改变前后系统频率范围几乎没有变化.值得注意的是该情况下参数变化空间非常大，当电阻、电感增大100倍，电容减小100倍时，即电路元件参数调整为：L＝1.7H，C2＝1nF，C1＝0.1nF，R＝150kΩ，有源二极管参数：R2＝R3＝22kΩ，R7＝220kΩ，R4＝R5＝2200kΩ，R6＝330kΩ时，系统混沌行为依然没有改变，其频谱图像如图8所示.但很明显的是电感电流的频谱幅值有了明显的变化.

图8 信号频谱图：（a）C1电压信号，（b）C2电压信号，（c）L电流信号Fig.8 Signal spectrum：（a）Voltage signal of capacitor C1（b）Voltage signal of capacitor C2（c）Current signal of inductor L

3 结论

综合以上分析，可以发现在典型蔡氏电路中，在一定参数空间内电路元件参数按前两种情况发生改变时，系统仍然能保持混沌状态，混沌系统的频率范围会随着动态元件的减小而增大.当电路系统的两种动态元件（电容和电感）发生相反的变化时（即第三种情况），混沌系统的频率范围几乎不变，但其参数变化空间比前两种情况的要大.第一种情况下，电路元件的动态范围为电容减小不大于100倍、电阻增大不大于10倍；第二种情况下，电路元件的动态范围为电容、电感均减小不大于10倍（注意，这里没讨论动态元件增大时的范围，是因为动态元件增大会导致频谱范围的缩小，不利于混沌系统的应用.）.

根据以上分析结果，在设计混沌电路时，可以参照已有混沌系统，通过改变不同元件的电路参数，设计出符合自己要求的实际混沌电路系统，这将丰富混沌电路设计途径，也可根据需要来改善所需混沌电路的特性，及提高混沌电路的实用化.这种方法我们将在忆阻器混沌电路中应用，据此给出电路实现时所需电路元件的较合理的参数值，或根据频率设计需求选择合适的参数值来改善系统的频谱特性.

1 Chua L O，Komuro M，Matsumoto T.The double scroll family-parts I and II.IEEE Transctions on Circuits and Systems，1986，33（11）：1073～1118

2 Itoh M，Chua L O.Memristor oscillators.International Journal of Bifurcation and Chaos，2008，18（11）：3183～3206

3 洪庆辉，曾以成，李志军.含磁控和荷控两种忆阻器的混沌电路设计与仿真.物理学报，2013，62（23）：230502（Hong Q H，Zeng Y C，Li Z J.Design and simulation of chaotic circuit for flux-controlled memristor and chargecontrolled memristor.Acta Physica Sinica，2013，62（23）：230502（in Chinese））

4 刘崇新.蔡氏对偶混沌电路分析.物理学报，2002，51（6）：1198～1202（Liu C X.Analysis of chua.sdual chaotic circuit.Acta Physica Sinica，2002，51（6）：1198～1202（in Chinese））

5 Muthuswamy B，Kokate P P.Memristor-based chaotic circuits.IETE Technical Review，2009，26（6）：417～429

6 Bao B C，Liu Z，Xu JP.Transient chaos in smooth memristor oscillator.Chinese Physics B，2010，19（3）：030510

7 Chua L O，Itoh M.Duality of memristor circuits.International Journal of Bifurcation and Chaos，2013，23（1）：1330001

8 Muthuswamy B.Implementing memristor based chaotic circuits.International Journal of Bifurcation and Chaos，2010，20（5）：1335～1350

9 Kocarev L.Chaos-based cryptography：a brief overview.Circuits and Systems Magazine，IEEE，2001，1（3）：6～21

10 Yang TA O，Chua LO.Channel-independent chaotic secure communication.International Journal of Bifurcation and Chaos，1996，6（12b）：2653～2660

11 Yang T，Wu C W，Chua L O.Cryptography based on chaotic systems.Circuits and Systems I：Fundamental Theory and Applications，IEEE Transactions，1997，44（5）：469～472

12 张丽丽，雷友发.一个三维非线性系统的混沌动力学特征.动力学与控制学报，2006，4（1）：5～7（Zhang L L，Lei Y F.The chaotic characters of a 3-dimensional non-linear dynamics.Journal of Dynamics and Control，2006，4（1）：5～7（in Chinese））

13 禹思敏，丘水生.一种语音混沌保密通信方案的研究与硬件实现.通信学报，2002，23（8）：105～112（Yu S M，Qiu SS.The research and hardware implementation of a scheme for chaotic secure communications.Journal of China Institute of Communications，2002，23（8）：105～112（in Chinese））

14 冉立新，陈抗生.蔡氏电路混沌信号频谱分布特征及其在电路设计中的应用.电路与系统，1998，3（1）：8～13（Ran L X，Chen K S.Spectrum distribution of chaotic signals in chuaps circuit and its application in circuit design.Journal of Circuits and Systems，1998，3（1）：8～13（in Chinese））

15 蒋国平，程艳云.蔡氏混沌非线性电路及其频率特性研究.电气电子教学学报，2002，24（5）：5～7（Jiang G P，Cheng Y Y.Study on chua′s nonlinear chaotic circuit and its frequency characteristic.Journal of EEE，2002，24（5）：5～7（in Chinese））

16 刘凌，苏燕辰，刘崇新.新三维混沌系统及其电路仿真实验.物理学报，2007，56（4）：1966～1969（Liu L，Su Y C，Liu C X.A new chaotic system and its circuit simulation.Acta Physica Sinica，2007，56（4）：1966～1969（in Chinese））

17 蔡国梁，谭振梅，周维怀.一个新的混沌系统的动力学分析及混沌控制.物理学报，2007，56（11）：6230～6236（CaiG L，Tan ZM，Zhou W H.Dynamical analysis of a new chaotic system and its chaotic control.Acta Physica Sinica，2007，56（11）：6230～6236（in Chinese））

18 袁地，侯越.一个三维非线性系统的混沌运动及其控制.控制理论与应用，2009，26（4）：395～399（Yuan D，Hou Y.Chaotic movement and its control of a three-dimensional nonlinear system.Control Theory＆App1ication，2009，26（4）：395～399（in Chinese））

19 周欣，王春华，郭小蓉.一个新的网格多翅膀混沌系统及其电路实现.物理学报，2012，61（20）：200506（Zhou X，Wang C H，Guo X R.A new grid multi-wing chaotic system and its circuit implementation.Acta Physica Sinica，2012，61（20）：200506（in Chinese））

20 Wang Z，Cang S，Ochola EO，etal.A hyperchaotic system without equilibrium.Nonlinear Dynamics，2012，69（1-2）：531～537

21 周小勇，乔晓华，朱雷.一类关联混沌系统及其切换与内同步机理研究.物理学报，2013，62（19）：190504（Zhou X Y，Qiao X H，Zhu L.A class of associated chaotic system，its switching and internal synchronization mechanism.Acta Physica Sinica，2013，62（19）：190504（in Chinese） ）