折叠翼的理论建模与实验研究*
胡文华 张伟 曹东兴
(北京工业大学机械工程与应用电子技术学院,北京 100124)
引言
从早期的木头帆布等高柔性结构,到高强度的金属结构,再到复合材料,飞行器经历了高柔性,高刚度再到柔性等阶段.时至今日,智能材料等日新月异的技术发展催生了以可控刚柔耦合结构为基础的可变体飞行器的研究热潮.几十年来,不同种类的飞机被设计出来应对不同的飞行任务,如运输机强调巡航性能,侦察机需要长时间滞空,而战斗机追求速度和敏捷性.而可变体飞行器可通过改变自身结构而获得不同气动外形来提高性能,达到全航程最优的飞行效益,适应多种飞行任务,例如在同一航程里实现短距离起降,高速机动以及低功耗巡航.很多国家对可变体飞行器进行了研究,但基本上都处于起步阶段.目前,几种主要的可变体飞行器设计方案是波音的连接翼方案、下一代公司的滑动蒙皮翼方案、雷神公司的伸缩翼方案、洛克希德马丁公司的Z型折叠翼方案和鸬鹚方案.
可变体飞行器涉及的学科很广,包括气动、材料、结构、控制和优化等,各方面的问题之间相互耦合,应当采取分散难点、各个突破、相互推进的方法,开展一些侧重于不同难点的项目,使得各个项目既能解决其所针对的难点问题,又能促进其他方面的研究.折叠翼是最有前景的可变体方案之一.但是,折叠翼比普通平直翼更容易发生扭转变形,可能导致低阶的弯曲和扭转耦合振动.本文主要针对以折叠翼为背景的折叠机构的力学性能开展工作,进行理论建模以及实验研究,初步探讨折叠翼的振动特性.
1 折叠翼的设计与制作
折叠翼可变体飞行器如图1(a)所示,能不断切换外形,其结构的时变和非线性特性严重,具有多体系统的特点,而且小尺度的变形又具有柔性体的特点,给可变体飞行器建模和飞行控制的研究带来了很大挑战.

图1 折叠翼Fig.1 Folding Wings
折叠翼实物制作如图1(b)所示,文章将折叠翼简化成折叠板结构,建立理论模型,设计制作了金属实验结构,利用力锤实验和LMS系统对结构进行了实验研究,得到了折叠板结构的模态和频率,分析了其振动特性.
2 力学建模
针对折叠结构的研究,早期的文献多集中于直角折叠梁结构.Nayfeh等[1]研究一个T型梁和质量块的耦合结构.Ji等[2]研究了带有集中质量块的T型梁的运动.Wang等[3]研究了端部带质量块的多梁结构.梁模型可以很好地近似板条等长宽比较大的结构,但对于长宽接近的结构,板模型能得到更为精确的结论.鉴于折叠翼的实际情况,用板理论研究会比用梁理论研究好,和实际模型的动力学特性更为接近.
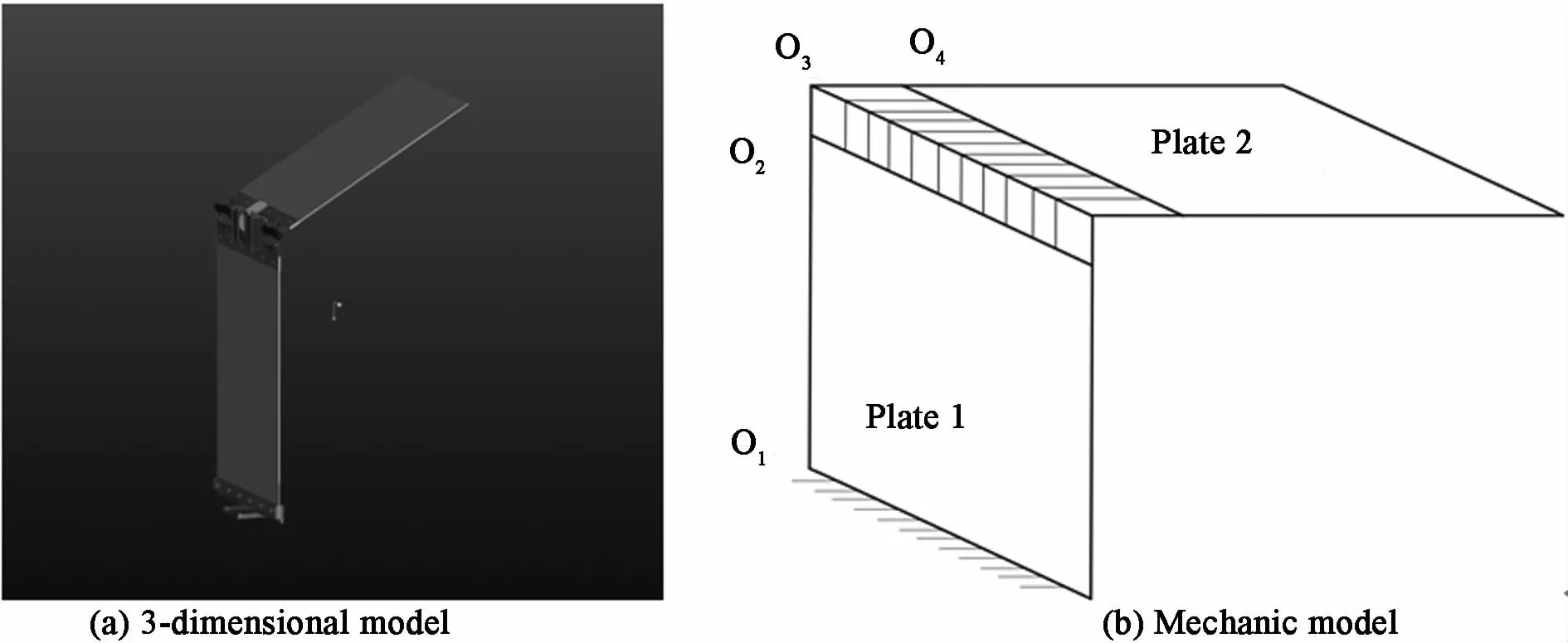
图2 简化模型Fig.2 Simplified mode
为研究折叠翼的振动特性,本文将其简化成折叠板机构,如图2所示.图2(b)中斜纹部分为钢夹具,夹具的两部分间可在任一角度时一定程度锁死,锁死后的夹角刚度用扭簧模拟.模型中,几个局部坐标系取在关键连接点处,如.与平直梁板等柔性结构相比,带一定角度的折叠结构的研究难度在于模态函数的选取更为复杂.
简单平直板结构的模态函数有比较成熟的形式,而由于折叠角的影响,多板折叠结构很难找到合适的模态函数,这使得很多学者不再拘泥于研究研究单板的思路中,而发展出各种针对特定模型的具体方法.Toshihiro等[4]研究了悬臂折叠板的自由振动,用悬臂梁和曲柄梁的模态函数的乘积作为折叠板振型函数来研究结构的自由振动,用Ritz法得到系统的频率方程和模态振型.Lai[5]用分段函数和Navier方法研究了V形折叠板的受迫振动响应,计算了简支V型板自用振动的频率方程,分析结果与有限元结果吻合得很好.Lee等[6]基于三阶剪切变形理论研究了复合材料层合折叠板,分了折叠角、边界条件、加载方式和铺设方式对暂态响应的影响.Attar等[7]将折叠翼模型固定于不同折叠角,用Ansys得到的振型离散动力学控制方程,研究了不同折叠角时折叠翼的气动弹性问题.郭述臻[8]对折叠翼飞机进行建模并运用计算流体力学软件进行数值计算.刘玮[9]等通过仿真分析,指出在鲁棒变增益控制器的作用下,变体飞行器在机翼折叠过程中波动较小.
为得到系统的控制方程,我们先给出该结构的位移场:

其中,ui,vi和wi分别是xi,yi和zi方向的位移,是局部坐标和全局坐标之间的转换矩阵,i=1,2,3,4.
假设系统受到小振幅激励,即F=ε2F.采用三阶剪切变形理论,设横向振动为小幅振动,其余两个方向的位移比横向位移小很多,则有

以矢量形式表示各部分中应变,

假设各部分均为各向均质材料,

系统的动能与势能为
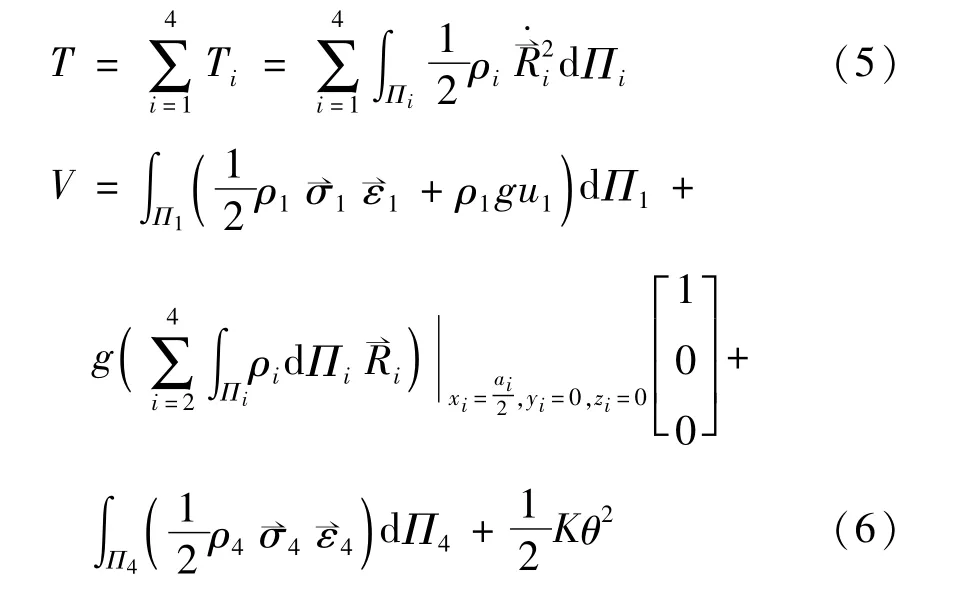
以伽辽金法截断各变量有

其中,Φ∈{wi,φix,φiy,ui0,vi0},n为截断阶数,qi(t)为全局自由度的时域变量,φi(x,y,z)是模态函数.对于简单结构,模态函数可以理论推导.复杂结构的模态函数通常是用数值方法或者实验方法得到.本文将以实验方法初步了解结构的低阶模态函数和可能存在的耦合共振频率.
将方程(1~7)代入哈密顿原理

由方程(8),考虑阻尼,可得到如下形式的控制方程:

式中,M、K、C分别为系统的质量矩阵、刚度矩阵和阻尼矩阵,为非线性项,X为激励项.给定参数,利用方程(9)可以计算结构的振动响应.
3 力学实验
梁、板等结构的各种理论研究都离不开力学实验.李银山[10]研究了轴对称周边固支圆板在简谐载荷作用下的非线性动力学行为,实验发现了混沌、对称破缺和超谐分岔等现象.Thomas[11]用接近圆板非对称模态所对应的频率的外载使系统做非线性受迫振动,该实验准确测量了两组不同参数时系统的振幅,实验显示系统振幅和相位是外激励频率的函数.Singhatanadgid等[12]以锤击实验分析了同材料以及不同材料的形状相似的不同尺寸的矩形板的固有频率之间的相似准则,发现工程上常用的相似原理也可以应用于振动响应实验.张伟[13]等设计了一种可伸缩机翼实验装置并进行振动实验,详细分析了在不同的外伸速度和收缩速度情况下,可伸缩机翼的横向振动响应.郭其威[14]等介绍了模态分析-试验体系工程研制流程在理论上的可行性,并以某缩比舱段为例,基于 Virtualab-Nastran软件平台,完整实施模态分析-试验体系过程.

表1 实验参数Table 1 Experimental parameters
按照上节所设计的折叠板结构,表1给出折叠板的材料和几何参数.第一行是板一的参数,第二行是板二的参数,第三行是钢夹具的参数.实验流程示意图如图3(a)所示,采用LMS公司的锤击实验模块对铝合金板钢连接的折叠板进行模态实验.图3(b)是实验现场.

图3 实验Fig.3 The experiment
实验中,控制力锤力度,以较小振幅激励结构,使式(9)线性化结论与实验相符.将实验结构固定在刚性基座上,连接好信号采集器、传感器、力锤和计算机,接上电源.加速度传感器粘贴到实验结构上,保证其与梁紧密接触.打开计算机和信号采集器,进入LMS,画出结构的几何模型,设置相应节点,完成相关参数(如信号通道设置,存盘路径,采样参数等)的设置.调整折叠角度,开始锤击实验.

图4 共振频率Fig.4 The resonant frequencies
图4中给出了实验测得结构前三阶频率随折叠角度变化的曲线,表示实验测得的前三阶频率.图4(a)显示二阶频率与2倍的一阶频率有相交点,如果系统有平方非线性项则该处存在一阶模态和二阶模态的1:2内共振点.图4(b)显示三阶频率与3倍的一阶频率也有相交点,如果系统有立方非线性项则该处存在一阶模态和三阶模态的1:3内共振点.
利用LMS进行分析,可以得到结构的振型.图5给出了90°折叠角的前三阶振型,由图可清晰看出一阶模态主要是板二的弯曲振动,二阶模态是板一的扭转振动和板二的弯曲振动的耦合,三阶模态主要表现为板二的扭转振动.由此可见,折叠板结构的全局模态即有可能主要表现为某部分的局部模态,也有可能为各部分以相似量级振动的耦合.利用本节所得到的振型作为方程(7)中的模态函数,可以得到系统的常微分运动控制方程,进而利用方程(9)研究系统动力学响应.

图5 折叠角90°的前三阶振型Fig.5 The first three modes at a 90°folding angle
4 结论
文章将折叠翼简化成折叠板结构,讨论用假设模态法分析折叠板,建立了理论模型,设计制作了折叠板的实验装置,利用LMS,通过锤击实验,得到了不同角度时结构的各阶频率和振型,指出随折叠角度的变化,结构可能出现不同模态之间的内共振,结构的模态可表现为局部振动模态,也可能是各部分以相似量级振动的耦合.实验中所得到的振型可以作为系统离散的模态函数,得到系统的常微分运动控制方程,进而研究系统的动力学响应.文章为对折叠结构的非线性动力学分析和刚柔耦合动力学分析提供一定的参考.
1 Nayfeh T A,Nayfeh A H,Mook D T.A theoretical and experimental investigation of a three-degree-of-freedom structure.Nonlinear Dynamics,1994,6(3):353~374
2 Ji JC,Yu L,Chen Y S.Bifurcation and amplitude modulated motions in a parametrically excited two-degree-of-freedom non-linear system.Journal of Sound and Vibration,1999,228(5):1125~1144
3 Wang F X,Bajaj A K.Nonlinear normal modes in multimodemodels of an inertially coupled elastic structure.Nonlinear Dynamics,2007,47(1-3):25~47
4 Toshihiro I,Gen Y,Yukinori K.Free vibration of a cantilever folded plate.Journal of the Acoustical Society of America,1984,76(6):1743~1748
5 Lai Y M,Yu W B.Analytical solution for forced vibration of a simply-supported V-shaped folded plate roof.Thinwalled Structures,2002,40(3):215~223
6 Lee SY,Wooh SC,Yhim SS.Dynamic behavior of folded composite plates analyzed by the third order plate theory.International Journal of Solids and Structures,2004,41(7):1879~1892
7 Attar P J,Tang D,Dowell E H,Nonlinear aeroelastic study for folding wing structures.The American Institute of Aeronautics and Astronautics,2010,48(10):2187~2195
8 郭述臻,郑祥明,尹崇,王鹏.折叠翼飞机的气动特性分析.航空工程进展,2013,4(3):358~363(Guo S Z,Zheng X M,Yin C,Wang P.Aerodynamic performance analysis of folding-wing aircraft.Advances in Aeronautical Science and Engineering,2013,4(3):358~363(in Chinese))
9 刘玮,陆宇平,殷明.折叠翼飞行器气动建模及变形稳定控制律设计.电子设计工程,2014,22(8):1~4(Liu W,Lu Y P,Yin M.Aerodynamic modeling and robust controller design for a foldingwing aircraft.International E-lectronic Elements,2014,22(8):1~4(in Chinese))
10 李银山.圆板振子超谐分岔和混沌运动的实验研究.实验力学,2001,16(4):347~357(Li Y S.Experiments on super-harmonic bifurcation and chaotic motion of a circular plate oscillator.Journal of Experimental Mechanics,2001,16(2):347~257(in Chinese))
11 Thomas O,Touze C,Chaigne A.Asymmetric non-linear forced vibrations of free-edge circular plates,part II:experiments.Journal of Sound and Vibration,2003,265(5):1075~1101
12 Singhatanadgid P,Songkhla A N.An experimental investigation into the use of scaling laws for predicting vibration responses of rectangular thin plates.Journal of Sound and Vibration,2008,311(1-2):314~327
13 张伟,张谦,曹东兴.可伸缩机翼结构设计与振动实验研究.动力学与控制学报,2011,9(4):326~330(Zhang W,Zhang Q,Cao D X.Structural design and vibration experimental investigation of telescoping wings.Journal of Dynamics and Control,2011,9(4):326~330(in Chinese))
14 郭其威,吴松,刘芳,赵阳东.航天器模态分析-试验体系工程实践研究.动力学与控制学报,2014,12(3):274~278(Guo QW,Wu S,Liu F,Zhao Y D.Research on engineering practice of modal analysis test of spacecraft.Journal of Dynamics and Control,2014,12(3):274~278(in Chinese) )

