基于逆阵更新方法的局部非线性结构频响分析*
云永旺 王珺 陈力奋 唐国安
(复旦大学力学与工程科学系,上海 200433)
引言
对于含有非线性连接的大型局部非线性结构,主频响应的稳定性及其稳态响应的幅值通常是结构设计中不容忽视的动力学特性.如航天器系统中,铰接结构的基频运动特性对航天器的在轨运动影响较大,是设计航天器时必须加以解决的问题之一[1].
E.Budak和 H.N.Ozguven[2],O.Tanrikulu和H.N.Ozguven等[3]针对含有非线性连接的多自由度系统,提出一种基于非线性力描述函数的迭代求解非线性主频响应的方法;在此基础上,M.B.Ozer等[4]进一步探索了系统的非线性参数识别问题,并在含有一个非线性连接参数的多自由度系统中实现了非线性类型和参数的仿真识别;Ozge Arslan等[5]则实验验证了上述非线性参数辨识的有效性;尉飞、郑钢铁等[6-8]将该方法应用于计算含有非线性连接的航天器的主频响应,通过选取结构中的非线性自由度、激励自由度和目标自由度,大幅度减少频响的计算规模.上述研究主要针对含有单个非线性连接位置(或参数)的结构,对于含多个(n≥2)非线性连接(或参数)的结构,目前相关的研究还很少看到.
Z.K.Peng等[9]基于 Volterra级数理论,提出了利用非线性输出频响函数辨识周期结构中非线性部件位置的方法;Z.Q.Lang等[10]将该方法应用于工程结构的故障诊断;姚红良等[11]基于非线性输出频响函数理论,针对因与外部接触而发生局部非线性的动力学系统,研究其频响分析及非线性位置的辨识.但其中的仿真算例都仅含有单个非线性连接.
对基于系统动柔度进行结构响应分析或参数辨识的研究,近年来逐渐受到国内外学者的关注.M.B.Ozer和 T.J.Royston[12]、S.S.Park和 J.Chae[13]各自提出了用动柔度识别耦合系统中连接参数的方法;Huajiang Ouyang等[14-15]尝试了采用动柔度方法解决非经典系统的振动控制问题;云永旺等[16]将动柔度修改方法应用于轴向杆件系统,并做了鲁棒性分析.上述研究目前还限于线性结构,但已经可以看出利用动柔度方法解决多自由度系统中多个参数辨识或修改问题的可行性.
本文针对含有多个非线性连接的结构,提出基于动柔度矩阵的拟线性分析方法,即逆阵更新(Inverse Matrix Updating Method,IMU)方法,将求解系统动柔度的高阶矩阵求逆问题转化为低阶矩阵的求逆,从而获得大型局部非线性结构主频响应的快速计算方法.仿真结果表明,本文的分析方法具有较好的稳定性,并能大幅提高大型局部非线性结构主频响应的计算效率.
1 逆阵更新方法的理论推导
1.1 含有非线性连接结构的响应分析
研究含有局部非线性连接的结构,其受外力激励时的振动微分方程如下:
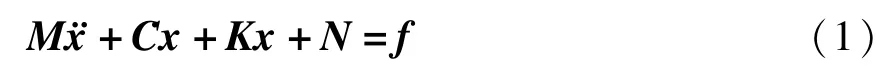
式中,M、C、K分别为结构的质量、阻尼和刚度矩阵,N为非线性内力,f为外激励力.
当系统受到简谐激励时,即:

系统响应可表示为:

局部非线性结构一般关注其主频响应,即:

其中,X为系统主频响应幅值向量.
对于受到简谐激励的系统,若假设其非线性内力也可以用简谐形式表示,即:

将式(2)、(4)、(5)代入式(1)中,于是系统振动微分方程转化为代数方程:

若将非线性内力幅值向量表示为形如[3]:

则式(6)可写成:

于是得到具有非线性连接结构的响应:

其中:

称为拟线性动柔度矩阵(Quasilinear Receptance Matrix)[3],类似于线性结构的动柔度,式(10)仅在弱非线性时成立.
式(10)中相应的线性部分动柔度矩阵记为:
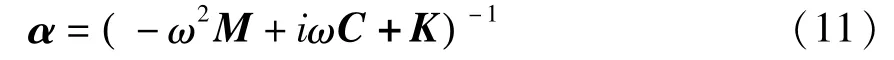
将式(11)代入式(10),得到

1.2 非线性内力的描述函数表示
文献[3]提出了利用描述函数表示非线性内力的方法.将式(1)中的非线性内力向量N的第k个元素表示成级数的形式:

其中,nkj表示非线性结构的两个连接位置k和j之间的非线性力(k≠j;当一端固结时则令k=j),并假设非线性力具有对称形式,且:

在式(5)的情形下,可将nkj用简谐形式近似表示为:

其中,非线性力的幅值Akj可由Fourier积分求得:

若定义系统主频响应幅值向量X中的任意两个分量之差为:

进一步令:
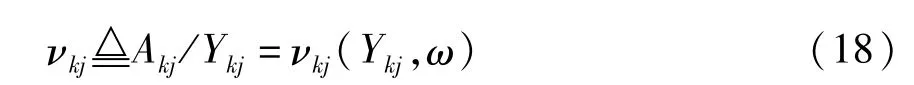
则称 νkj为非线性力 nkj的描述函数[3].
将式(18)代入式(15),得到:

进一步代入式(13),得到:

对比式(5)和式(20),可得:

由式(21),可推导得到式(7)中Δ的表达式:

称Δ为拟线性矩阵[3].
1.3 逆阵更新(IMU)方法
由式(9)和式(10)可知,求解含有非线性连接的系统频响,实质上是矩阵求逆的过程,对于大型结构,则是高阶矩阵求逆的问题.
在大型局部非线性结构中,非线性连接通常仅跟很少量的自由度有关.以含有2个非线性连接的结构为例(如图1所示),其拟线性矩阵Δ表示为:

图1 含有2个非线性连接结构的质量-弹簧系统Fig.1 The mass-spring system with two nonlinear connections

上式进一步可写成:

其中,

将式(24)代入式(12),可得:
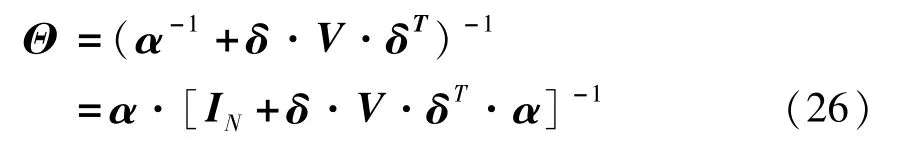
式中N为结构自由度数.通过矩阵运算,将式(26)进一步写成:

式中m为所连接的非线性结构的数目.一般来说,m≪N,则式的高阶求逆问题转化成式的低阶求逆,称之为逆阵更新(Inverse Matrix Updating Method,IMU)方法.不难发现,在局部非线性结构中,如果线性部分的频响特性α可以通过实测或有限元方法获得,有限的非线性连接位置δ和模型V已知,则由式可计算得到局部非线性结构的主频响应.
2 逆阵更新(IMU)方法求解系统频响的数值计算
由式(27)可知,若线性部分的频响特性及非线性连接特性已知,即可求解系统的频响.由于V(或Δ)同时又与响应X相关,因此在数值计算中,通常需要构造迭代方法来进行.
将式(27)代入式(9),构造迭代公式:

上式中,Δω为迭代步长,ωl,h为扫频的最低或最高的频率.在实际计算中,迭代公式(28)在共振频率附近通常较难收敛,一般需引入加权因子λ,构造迭代为[3]:
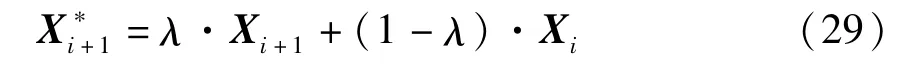
加权因子λ的值一般可取0~0.5.
3 仿真算例
3.1 含有立方非线性的单自由度系统频响分析
如图2所示的单自由度(Single degree of freedom,SDOF)系统,质量块与固壁间连接的是立方非线性刚度(Cubic stiffness)弹簧,系统特性参数如下:


图2 含有立方非线性的单自由度系统Fig.2 The single degree of freedom system with a cubic stiffness spring
当所加激励 F=200N时,采用龙格-库塔法(Runge-Kutta)求解,取3个振动周期后的稳态响应,得到的频响曲线如图3所示,计算过程用时约230秒(HP电脑,CPU为4GHz).

图3 龙格-库塔法计算的单自由度系统频响曲线Fig.3 The frequency response of the SDOF system by the Runge-Kuttamethod
同样的参数条件下,采用本文所述的迭代方法计算得到的系统频响如图4所示,计算过程用时0.75秒(同样的电脑).

图4 动柔度迭代方法计算的单自由度系统频响Fig.4 The frequency response of the SDOF system by IMU
由图3和图4的频响曲线可以看出,对于具有立方非线性弹簧的单自由度系统,采用传统的龙格-库塔方法和本文提出的IMU方法都能得到较为理想的计算结果.在相同参数条件下,采用IMU方法的计算效率显著提高.
3.2 单非线性连接的多自由度系统频响分析
研究如图5所示的含有单个非线性连接的多自由度(Multi-Degree-of Freedom,MDOF)轴向振动系统,立方非线性弹簧位于固壁与第1个质量块之间.

图5 含有单个非线性的多自由度轴向振动系统Fig.5 A ten DOFaxial vibration system with single nonlinear connection
该振动系统的特性参数如下:

当系统在第1个质量块上受到简谐力作用时,激励力幅值为f0=175N,采用(IMU)方法计算该局部非线性系统的频响,得到第1个质量块上的频响曲线如图6所示.
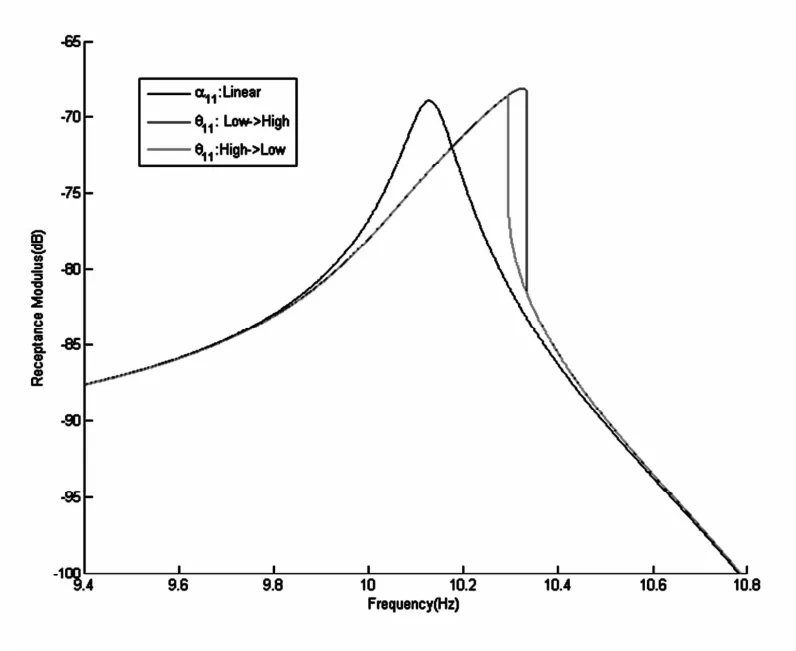
图6 含有单个非线性弹簧(连接固壁)的轴向振动系统的频响曲线Fig.6 The frequency response ofthe axial vibration system with single nonlinear connection between the 1th coordinate and the ground
改变非线性弹簧的连接位置,将非线性弹簧连接在第1个和第2个质量块之间,激励分别作用在第1个质量块和第2个质量块上,激励力幅值为f0=75N.采用逆阵更新(IMU)方法计算系统响应,分别得到Θ12和Θ21的频响曲线如图7所示.
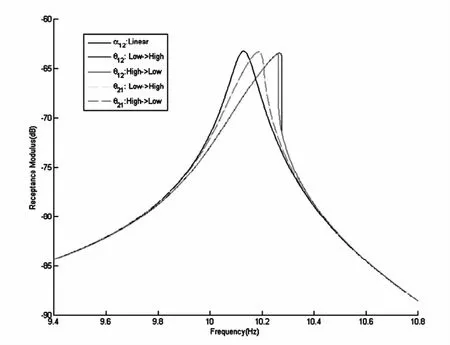
图7 含有单个非线性弹簧的轴向振动系统的频响曲线Fig.7 The frequency response of the axial vibration system with single nonlinear connection between the 1th and the 2nd coordinates
从图6和图7的频响曲线可以看出,采用IMU方法,在系统第一阶共振频率附近,从低频到高频和从高频到低频分别进行迭代计算,系统的频响特性均出现明显的非线性现象(弹簧硬化).上述结果与文献[3]的计算结果基本一致.计算中均引入加权因子 λ=0.3.
3.3 含有多个非线性连接的轴向振动系统频响分析
研究含有三个非线性连接(立方非线性刚度弹簧)的轴向振动杆件,如图8所示.

图8 含有三个非线性连接的轴向振动杆Fig.8 An axial vibration rod with three nonlinear connections
该轴向振动杆两端固支,特性参数如下:

三个立方刚度非线性弹簧的描述函数为:
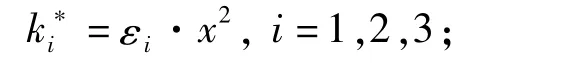
其中:

比例阻尼:c=ηk,η=0.01.
非线性弹簧连接位置:

激励位置:Lq=1.8m;幅值 f0=8.0×103N;
响应位置:Lp=1.8m.
将连续杆件系统离散成N自由度质量-弹簧系统(集中质量法),如图9所示.
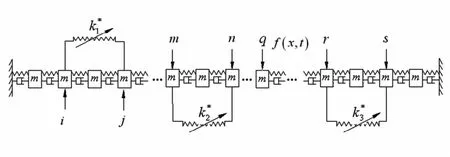
图9 含有三个非线性连接的轴向振动杆离散系统Fig.9 The discrete axial vibration system with 3 nonlinear connections
N分别取 150,200,300,400,500,600时,连续系统和离散系统的固有频率如表1和图10所示.

表1 轴向振动系统的前5阶固有频率Table 1 The first5 order natural frequencies of the axial vibration system

图10 轴向振动系统的第1阶固有频率曲线Fig.10 The first order natural frequency of axial vibration system
从表1和图10可以看出,随着离散自由度数不断增加,离散系统的固有频率不断逼近连续系统的固有频率值.当N=300时,离散系统第1阶固有频率与连续系统的第1固有频率误差仅为0.3%.
采用IMU方法,在系统的第1阶共振频率附近从低频到高频及从高频到低频分别进行迭代计算,得到局部非线性系统的自频响特性,如图11所示.不难看出,具有明显的非线性现象(弹簧硬化),且随着离散自由度数的增加,频响曲线的跳跃区间(频率)逐渐收敛.由此说明,该方法具有很好的稳定性.
4 结论
本文针对局部非线性系统,提出了基于逆阵更新(IMU)的分析非线性主频响应的快速计算方法.该方法采用动柔度矩阵描述系统频响特性,通过矩阵运算将求解系统动柔度的高阶求逆问题转化为低阶矩阵求逆,在数值计算中利用加权迭代,得到非线性系统的频响.
对含有立方非线性的单自由度系统及含有单个和多个非线性连接的多自由度系统的仿真算例都表明,(IMU)方法不仅计算效率高,而且算法收敛性好,计算结果稳定,特别适合于大型局部非线性结构.本方法针对其他非线性类型(如间隙非线性等)或其它结构类型(如梁、板等)的仿真分析和实验验证正在继续研究中.

图11 不同离散自由度的频响 hpq曲线(Lq=1.8m,Lp=1.8m,自频响)Fig.11 The receptances of the axial vibration system with different discrete DOF
1 王巍,于登云,马兴瑞.航天器铰接结构非线性动力学特性研究进展.力学进展,2006,36(2):233~238(WangW,Yu D Y,Ma X R.Advances and trends of nonlinear dynamics of space joint-dominated structure.Advances in Mechanics,2006,36(2):233~238(in Chinese))
2 Budak E,Ozguven H N.Iterative receptance method for determining harmonic response of structures with symmetrical non-linearities.Mechanical Systems and Signal Processing,1993,7(1):75~87
3 Tanrikulu O,Kuran B,Ozguven H N,Imregun M.Forced harmonic response analysis of non-linear structures using describing functions.AIAA Journal,1993,31(7):1313~1320
4 Ozer M B,Ozguven H N,Royston T J.Identification of structural non-linearities using describing functions and the Sherman-Morrison method.Mechanical Systems and Signal Processing,2009,23(1):30~44
5 Arslan O,Aykan M,Ozguven H N.Parametric identification of structural nonlinearities from measured frequency response data.Mechanical Systems and Signal Processing,2011,25(4):1112~1125
6 尉飞,郑钢铁.具有非线性连接的航天器非线性振动分析.振动工程学报,2009,22(4):329~334(Wei F,Zheng G T.Nonliear dynamics of spacecraft with nonlinear joints.Journal of Vibration Engineering,2009,22(4):329~334(in Chinese))
7 尉飞,白绍竣,张静,郑钢铁.一种求解局部非线性结构稳态响应的方法.应用力学学报,2009,26(4):793~797(Wei F,Bai SJ,Zhang J,etal.Evaluation for steady state response of systems with local nonlinearities.Chinese Journal of Applied Mechanics,2009,26(4):793~797(in Chinese))
8 Wei F,Zheng G T.Nonlinear vibration analysis of spacecraftwith localnonlinearity.Mechanical Systemsand Signal Processing,2010,24(2):481~490
9 Peng Z K,Lang ZQ,Chu F L,Meng G.Locating nonlinear components in periodic structures using nonlinear effects.Structural Health Monitoring,2011,9(5):401~411
10 Lang ZQ,Park G,Farrar CR,et al.Transmissibility of non-linear output frequency response functions with application in detection and location of damage in MDOF structural systems.International Journal of Non-Linear Mechanics,2011,46(6):841~853
11 姚红良,韩清凯,冯霏,等.多自由度局部非线性系统频域响应及非线性位置的辨识方法.动力学与控制学报,2011,9(2):107~110(Yao H L,Han Q K,Feng F,et al.NOFRF of the locally non-linear MDOF system and the detection method of the nonlinearity position.Journal of Dynamics and Control,2011,9(2):107~110(in Chinese))
12 Ozer M B,Royston T J.Application of Sherman-Morrison matrix inversion formula to damped vibration absorbers attached to multi-degree of freedom systems.Journal of Sound and Vibration,2005,283(3-5):1235~1249
13 Park SS,Chae J.Joint identification of modular tools using a novel receptance coupling method.The International Journal of Advanced Manufacturing Technology,2008,35:1251~1262
14 Ouyang H J,Baeza L,Hu SL.A receptance-based method for predicting latent roots and critical points in frictioninduced vibration problems of asymmetric systems.Journal of Sound and Vibration,2009,321(3-5):1058~1068
15 Ouyang H J.Prediction and assignment of latent roots of damped asymmetric systems by structural modifications.Mechanical Systems and Signal Processing,2009,23(6):1920~1930
16 云永旺,陈力奋,唐国安.基于动柔度修改的轴向振动控制系统鲁棒性分析.振动与冲击,2009,28(12):146~150(Yun YW,Chen L F,Tang G A.Robustness analysis of axial vibration controlbased on receptance modification method.Journal of Vibration and Shock,2009,28(12):146~150(in Chinese) )

