多弹头导弹反推分离的一种组合控制方法
郝子龙 刘新建
(1.西北核技术研究所,西安 710024)(2.国防科学技术大学航天科学与工程学院,长沙 410073)
引言
多体分离控制问题在“一箭多星”发射、分导式多弹头导弹(MIRV)、组合航天器分离等领域具有重要的意义.喷气反推分离是大气层外的一种主要分离方式,分离过程不仅要求在一定的时间内达到安全距离,而且不能发生碰撞.
国内外这种分离控制方式主要有两种:一种是把反推分离力对被分离体的姿态影响当成小干扰,被分离体的喷嘴姿态控制采用已较为成熟的方法,如相平面 PD开关控制、变结构控制[1-3]、最优控制[4]、自适应控制[5]和 H2/H∞控制[6]等方法.另一种是考虑反推分离力的影响,优选一种反推分离开关时序,以便对被分离体的姿态扰动最小,这种方式相比第一种的分离控制性能要好,提高了分离可靠性,工程上常采用,但这种方式事先要就各种可能工况进行大量的仿真优化才能得到最佳分离时序,另外其在不可预测的大干扰下鲁棒性和可靠性有待提高.
因为最佳分离时序对被分离体姿态的作用本质上是一种开路,为此对最佳分离时序策略进行改进,提出一种反推分离力参与姿态闭环控制的分离方法,即反推分离的开关是由姿态反馈测量并与阈值比较来决定自动打开与关闭,在开关打开的时间段内,系统受反推力分离,关闭就没有分离力,惯性分离,下面通过仿真算例阐明其可行性和正确性.
1 分离系统动力学模型
1.1 模型描述
为了方便分析,对模型进行简化:假设分离系统是由两个分离体和一个被分离体组成,其中包含两个独立的运动子系统:分离出的分离体(分离体1)和未分离的分离体(分离体2)与被分离体组成的结构(组合体).
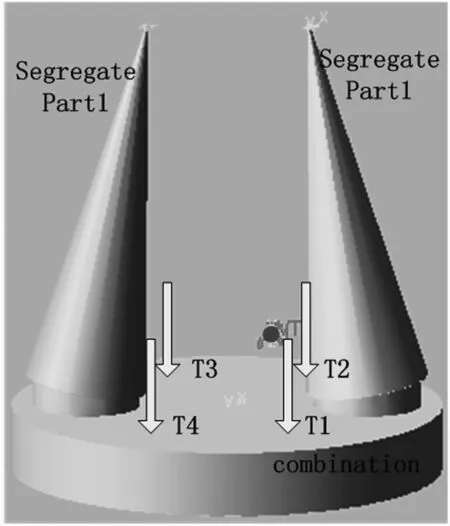
图1 分离系统受力情况Fig.1 Force conditions of separation system
分离过程中,组合体(被分离体)受到的反推分离力沿未分离时组合体重心两侧均匀分布,分离反推力假设为四个,其分布情况如图1所示:
由于反推分离力T3和T4的力臂要大于T1和T2的力臂,则T3和T4对组合体质心的力矩也较大,组合体分离过程中向左侧偏转,可能引起与分离体1的碰撞.
1.2 坐标系
(1)惯性坐标系O-XYZ
选取分离0时刻与组合体中心对称的体系重合的坐标系为惯性坐标系.
(2)分离体质心坐标系 O1-x1y1z1和 O2-x2 y2 z2
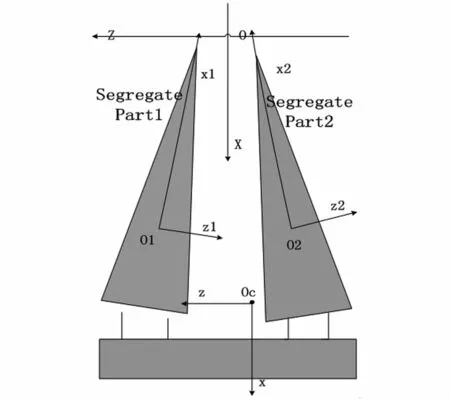
图2 分离系统坐标系情况Fig.2 Coordinate system of separation system
图2所示,选取各自中心对称的体坐标系为分离体坐标系,x轴为对称纵轴,按右手法则确定y轴方向.
(3)组合体质心坐标系Oc-xyz
选取原点为组合体重心,与惯性坐标系平行的坐标系为组合体质心坐标系.
(4)坐标系转换
根据坐标系的转换关系[7],对坐标系进行转换,以使所有运动状态表示在一个坐标系中.假设分离体1质心坐标系到惯性坐标系的转换矩阵为A1,分离体2坐标系到惯性坐标系的转换关系为A2,组合体质心坐标系到惯性坐标系的转换矩阵为Ac.
1.3 受力分析
(1)分离体1受力情况
分离解锁后,大气层外分离体1只受重力的作用,作用点为质心,重力对质心的力矩为0,则在惯性坐标系中:


(2)组合体受力分析
组合体在分离过程中除了受到重力的影响,还要受到反推分离力的作用.假设,受到四个反推分离力T1、T2、T3和T4的作用,它们在组合体质心坐标系中的位置分别为 →r1c、→r2c、→r3c和 →r4c.
在四个反推力和重力共同作用下,组合体的受力为:

组合体受到的对质心的合力矩为:

1.4 动力学和运动学方程
(1)质心运动学和动力学方程
分离体与组合体的质心运动都遵循质心动力学与运动学方程:

若m为分离体1质量时,表示分离体1质心动力学方程;
若 m为组合体质量时,表示组合体的质心动力学方程.
(2)欧拉姿态动力学方程
用欧拉动力学方程来描述分离体与组合体以质心为定点的转动.全量欧拉动力学方程组[7]为:

其中Mc为组合体的喷嘴控制力矩,MT为反推分离力对组合体的合力矩,I为惯量张量,ω为角速度矢量.
由矢量A的绝对导数公式得到全量欧拉动力学方程为:
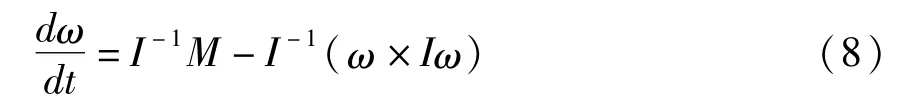
为了防止大机动角控制时欧拉角引起的奇点问题,用四元数来表示欧拉角,欧拉角与四元数q0,q1,q2,q3的关系[9]可表示为:
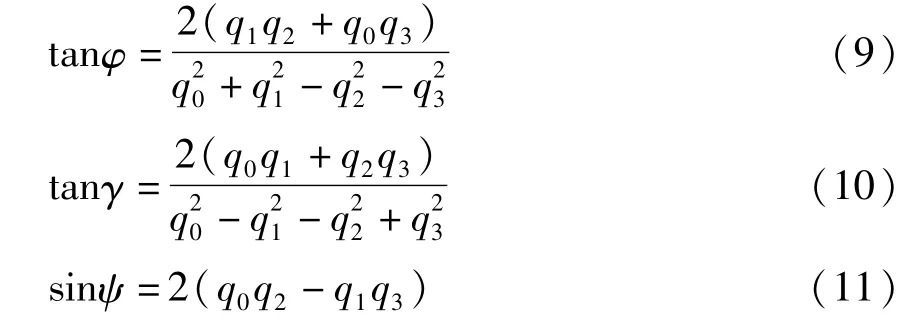
其中,φ为俯仰角,ψ为偏航角,γ为滚动角.
2 分离体分离间距计算方法
分离体之间的最小间距计算是分离动力学与控制仿真的一个重要环节.根据分离体模型的规范化特点将分离体简化为圆台体,使两分离体之间的最短距离计算简化为两个空间圆台体之间的最小距离的计算,再转化为空间一点到圆台曲面的距离计算,具体参考文献8.
3 组合体的分离姿态控制策略
3.1 PD开关控制
通常组合体具有喷嘴开关闭环控制系统,控制其俯仰、偏航和滚动角.工程上常用相平面PD关控制,这里依然采用.
组合体姿态PD开关控制律环节根据姿态跟踪偏差产生对应各姿态喷管的开关控制指令.
基本控制律为:

其中,φ为偏航角,ψ为俯仰角,γ为滚动角.P和D分别为比例系数和微分系数,设定合适的比例微分系数和姿控喷管的开关门限,对组合体分离过程的姿态进行控制,使分离过程中组合体的姿态变化较小.
3.2 分离反推力参与的开环时序控制方法
为了弥补PD开关控制的不足,同时利用反推分离力对姿态的影响,工程上一般采用分离反推力参与的开环时序控制与PD开关控制共同作用对分离过程姿态进行控制.
分离反推力开环控制方法是利用网格法选取最优时序t1和t2,使组合体重心两侧的反推分离喷管 T3和 T4在 t1<t<t2时关闭,在 t≤t1或 t≥t2时四个反推喷管都打开,加速分离,直到到达分离距离反推喷管都关闭.
3.3 分离反推力参与的闭环控制策略
反推分离力参与的闭环控制策略也是在PD控制的基础上利用反推分离力进行姿态控制的方法,不同的是,反推分离力由最佳开关时序策略改为闭路反馈控制策略,作为喷嘴姿态控制的补充,图2所示,如果T3,T4或T1,T2同时开启或关闭,就只影响组合体绕y轴的偏航角.
由于分离体1的姿态在初始角速度扰动下是改变的,理论上要求出组合体对分离体1的相对姿态角,作为反推分离力闭环控制的反馈信息.
相对滚动角和相对俯仰角在分离过程中对碰撞的影响很小,碰撞主要是在具有较大的初始偏航角速度的情况下发生的,因此,反推分离力的开关闭环控制只要控制相对偏航角的状态,就能有效避免碰撞的发生.由同时加载T1,T2或同时加载T3,T4来控制组合体的偏航角.设定相对偏航角门限threshold,控制反推分离力的加载情况.
门限情况:
当相对偏航角Δψr>threshold,,则要减小组合体的偏航力矩,需要只施加反推分离力T1,T2;
当相对偏航角Δψr<-threshold,则要增大组合体的偏航力矩,需要只施加反推分离力T3,T4;
当相对偏航角 threshold≤Δψr≤threshold,则分离过程可以保证不碰撞,不需要辅助姿控,这时同时施加反推分离力 T1、T2、T3、T4,加速分离.
3.4 相对姿态角计算
以分离体与被分离体间的相对姿态角及姿态角变化率为状态空间变量写状态空间方程,以被分离体质心主惯量坐标系为计算坐标系列写相对姿态运动方程.相对姿态角求解过程如图3所示:

图3 相对姿态角的求解过程Fig.3 The solving process of relative attitude angle
惯性系(图中表示为I)中分离体角速度为ω1,被分离体角速度ω2,惯性系到被分离组合体质心坐标系(图中表示为E)的四元数为λ2,惯性系到上面体1质心体坐标系(图3中表示为E′)的四元数为λ1.被分离体B相对上面体1的角速度在惯性系中表示为Ω,在被分离体质心坐标系中表示为ΩE,相对四元数 λ.
根据四元数坐标转换公式[9],四元数运动学方程,得到相对姿态角的求解公式:

在扰动角速度不大情况下,也可以直接采用绝对姿态角信号,从而简化分离反馈控制.
4 分离过程仿真与分析
利用MATLAB/Simulink模块对分离过程动力学模型进行仿真,对不同的控制方式下分离过程结果进行分析对比.假设组合体质心位移达到1.8米时分离结束,关闭分离反推力.
(1)绝对姿态角反推力开环时序控制参与的姿态控制分离过程中,通过对反推力分离时序进行优化,得到时序为 t1=0.5s,t2=1s时分离间距最大.
(2)相对姿态角反推力闭环控制参与的姿态控制分离过程中,设定阈值threshold为1°分离情况进行仿真,分别对相对姿态角情况下和绝对姿态角情况下的闭环分离过程进行仿真.
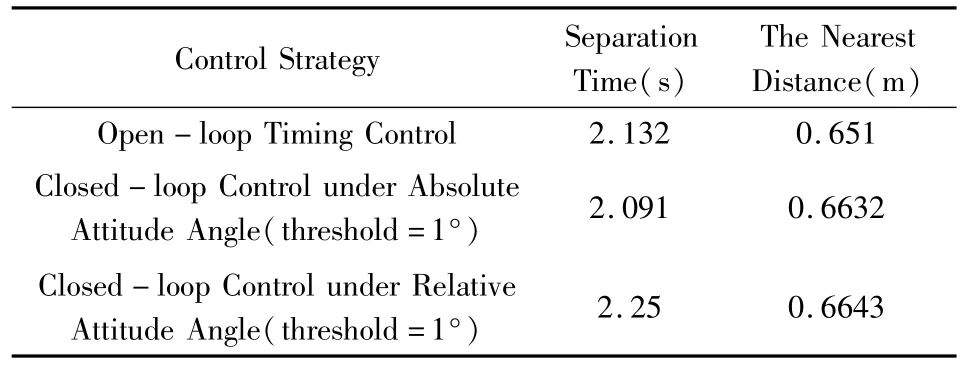
表1 无初始姿态偏差情况下的分离过程Table 1 Separation process without initial attitude deviation
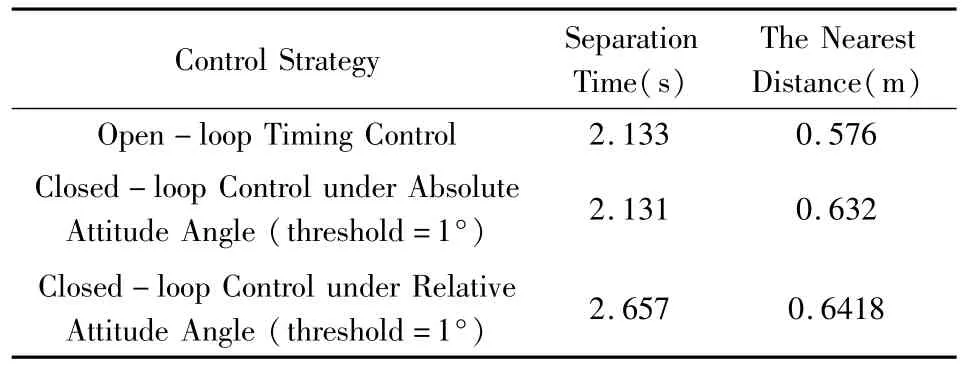
表2 有初始姿态偏差情况下分离过程Table 2 Separation process with initial attitude deviation
分别对无初始姿态偏差的情况和组合体具有初始偏航角速度为3°/s,分离体具有初始偏航角速度-3°/s情况下分离过程进行仿真,仿真结果如表1和表2所示.
由表1和表2可知,相对姿态角反推力闭环控制的分离过程比绝对姿态角反推力开环时序控制的分离方式和绝对姿态角反推力闭环控制的分离过程在有初始姿态偏差的情况下更安全.

图4 大偏差情况分离时序控制方式Fig.4 The separation with large deviations under timing control

图5 大偏差情况下分离闭环控制方式Fig.5 The separation with large deviations under closed-loop control
在分离过程中出现大的扰动时,可能会有大的初始姿态偏差出现.假设,分离体1初始偏航角速度为 -15°/s,组合体初始偏航角速度为 20°/s.分别对两种姿态控制方式下的分离过程进行仿真.
绝对姿态角反推力开环时序控制方式的分离过程如图4所示.
分离过程中分离体与组合体之间相对分离距离出现了零值,即分离过程发生了碰撞.
阈值为1°的相对姿态角反推力闭环控制方式分离过程仿真如图5:
即使在偏差较大的情况下分离过程也没有出现碰撞,显然较开环时序控制的分离过程更加安全,鲁棒性更好.
5 结论
为了解决反推分离力时序控制方式鲁棒性较差的问题,提出了一种反推分离力同时参与组合体姿态闭环的控制策略.仿真分析表明,这种策略比最佳时序控制方式的鲁棒性要好、对分离时序不需要事先进行大量的参数优化,安全性更高,鲁棒性更强,而且方法简单,工程可实现性好,可应用于导弹分导,“一箭多星”发射等的分离控制中.
1 陈宏钧,王卓军,周荻等.飞行器变结构姿态控制的研究.哈尔滨工业大学学报,1997,29(6):11~12(Chen H J,Wang Z J,Zh D,et al.Research on variable structure attitude control of aircraft.Journal of Harbin Institute of Technology,1997,29(6):11~12(in Chinese))
2 Bartoszewicz A.Timing-varying sliding modes for second and three order systems.IEEE Proc.Control Theory Application,1996,143(5):455~462
3 李俊峰,林原.重力梯度卫星大角度姿态机动的变结构控制.动力学与控制学报,2003,1(1):66~69(Li J F,Lin Y.Sliding mode control for large angle maneuvers of gravity gradient stabilized satellite.Journal of Dynamics and Control,2003,1(1):66~69(in Chinese))
4 林枫,刘国刚.最优控制与姿控喷流在导弹姿态控制中的应用.航天控制,2004,3(22):20~22(Lin F,Liu G G.Application of optimal control using direct side force in missile attitude control system.Aerospace Control,2004,3(22):20~22(in Chinese))
5 Thawar T Arif.Adaptive control of rigid body satellite.International Journal of Automation and Computing,2008,8,05(3):296~306
6 Bernstein D S,Haddad W M.LQR control with an h-infinity performance bound:a riccati equation approach.IEEE Transactions on Automatic Control,1989,34(3):293~305
7 孙世贤,黄圳圭等.理论力学教程.长沙:国防科技大学出版社,2005(Sun SX,Huang ZG.Theoretical mechanics tutorials.Changsha:National University of Defense Technology Press,2005(in Chinese))
8 张岩,唐乾刚,张翼,孔铁全.导弹分离碰撞判断与最小距离快速算法.战术导弹技术,2003,4:41~46(Zhang Y,Tang Q G,Zhang Y,Kong T Q.Verdicting collision and calculating the nearest distance during missile deparating.Tactical Missile Technology,2003,4:41~46(in Chinese))
9 黄圳圭.航天姿态动力学.长沙:国防科技大学出版社,1997(Huang Z G.Aerospace attitude dynamics.Changsha:National University of Defense Technology Press,1997(in Chinese) )

