两档输电线路间的非线性耦合振动特性研究*
谢献忠 龙昊 李丹
(湖南科技大学土木工程学院,湘潭 411201)
引言
输电线路是属于悬索结构中的大跨度高柔结构,在承受自重、覆冰等静荷载,风、地震等动荷载下具有明显的非线性行为[1].正是由于其特殊性,输电线路振动是非线性振动领域中非常典型的问题.国内外绝大多数学者在研究输电线路振动问题的理论建模时,往往只考虑了单档输电线的振动情况[2-3],本文在以往研究的基础上,考虑档与档之间的耦合振动,建立了更为完善的力学分析模型,并推导了两档输电导线以及悬垂绝缘子串的非线性振动方程.利用数值分析软件计算出系统的位移时程曲线,通过对不同工况下的两档输电导线及垂悬绝缘子串的振动进行比较研究,从而得出了两档输电导线的非线性耦合振动特性和共振特性.
1 两档输电线路非线性耦合振动的力学模型
输电线路在荷载作用下会发生面内和面外的振动,为了便于研究,又能体现问题的本质,本文只研究输电线路在面内的非线性振动,不考虑面外和扭转方向的振动,并作以下基本假设:
(1)采用固定铰支座模拟耐张塔对线的约束作用,输电导线与悬垂绝缘子串的连接为理想铰接,不计输电导线的抗弯刚度、抗扭刚度和剪切刚度.
(2)输电线重力垂度曲线为抛物线.
(3)考虑几何非线性,但输电导线的本构关系满足胡克定律.
本文建立的力学分析模型如图1所示.
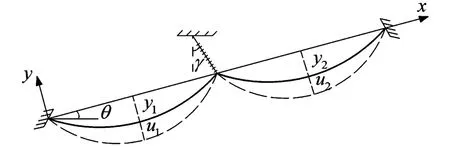
图1 两档输电导线耦合振动力学模型Fig.1 Mechanical model of coupled two-spans transmission line
不失一般性,取第一档导线微元体作为研究对象,利用牛顿定律可建立输电导线的运动方程
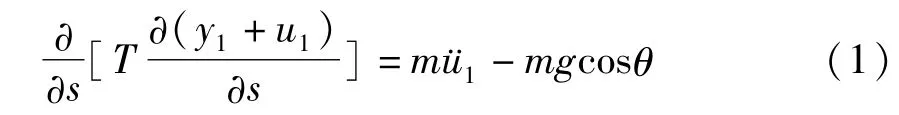
式中y1表示输电线静平衡时的曲线,u1表示偏离平衡位置的位移,T表示导线切向拉力,m表示输电线单位长度的质量,ü1表示位移对时间的二阶导数,s表示输电导线的弧长坐标,θ表示传输角度.
考虑重力平衡,式(1)可以表示为
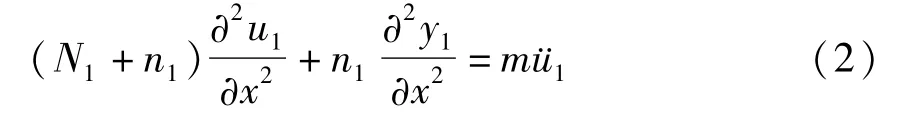
式中N1为初始切向拉力,n1为切向动拉力.同时考虑输电导线的垂度、几何非线性和端部位移,n1可以表示为
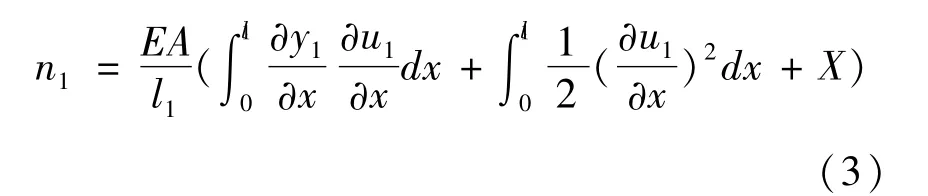
式中E表示输电导线的综合弹性模量,A表示输电导线的横截面积,l1表示输电导线的长度,X表示输电导线悬挂点摆动的的水平位移且

式中a为悬垂绝缘子串的长度,γ为悬垂绝缘子串的偏转角.
根据基本假设(2),输电导线在静平衡条件下的垂度曲线可表示为
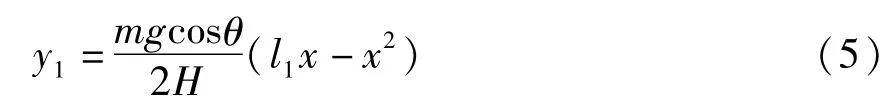
式中H为输电导线的水平拉力,m为导线单位长度的质量.
假定
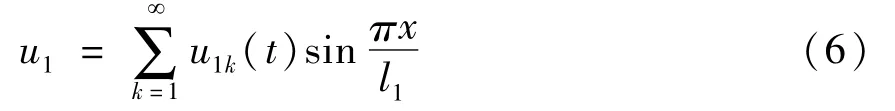
在输电导线的振动中基本模态占主要地位,故本文只研究k=1的情况,即

以下用 u1代表u11,将式(4),(5),(7)代入式(3)化简可得
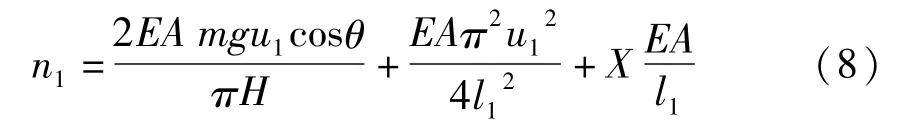
将(8)式代入到(2)式,并考虑阻尼,可以得出第一档输电线路的振动微分方程
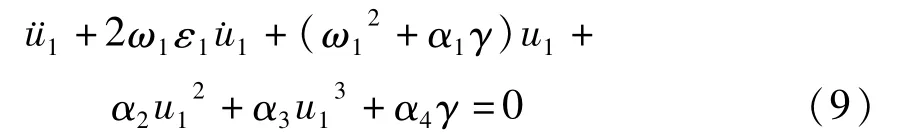
其中ε1为输电导线的阻尼比,ω1为考虑垂度影响下的的输电导线的振动频率,α1~α4为振动方程的系数,且

同理,第二档输电导线的动拉力、振动微分方程分别为
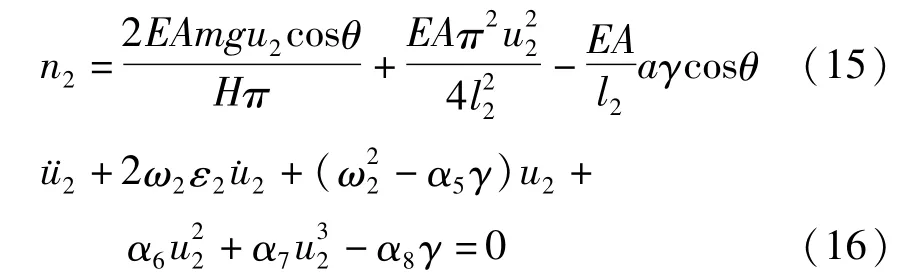
方程(16)中的各参数与方程(9)中的对应参数具有相同的形式,只需将式(10)~(14)中 l、N的下标由1换成2即可.
以图2所示绝缘子串为研究对象,建立其摆动的动力学方程.

图2 悬垂绝缘子串摆动的力学模型Fig.2 Mechanical model of insulator string rotation
在实际工程中,垂悬绝缘子串的摆角γ较小,因此,根据牛顿定律,悬垂绝缘子串的摆动方程为
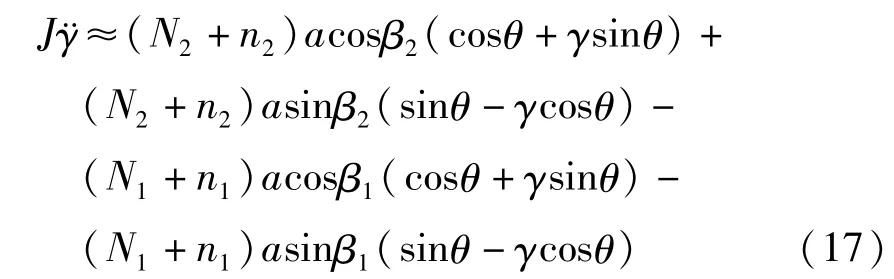
式中a为悬垂绝缘子串的长度,J为悬垂绝缘子串的转动惯量,β1,β2分别为左、右两档输电导线在悬挂点处的切线方向与x轴的夹角,且

将式(8),(15),(18),(19)代入方程(17),并考虑阻尼,可得出悬垂绝缘子串的摆动方程
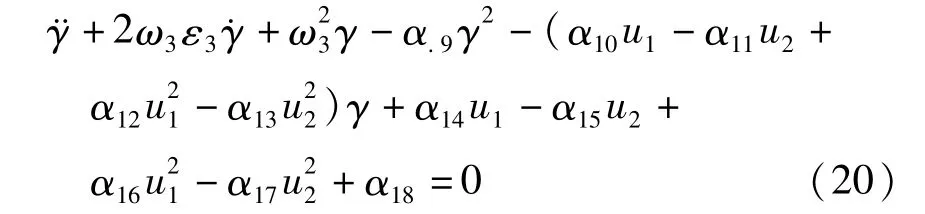
式中ε3为绝缘子串摆动的阻尼比,ω3为绝缘子串的振动频率,α9~α17为方程系数,且

方程(9)、(16)、(20)即为两档输电线路与悬垂绝缘子串耦合振动的非线性动力学方程组.
2 算例
2.1 算例1
输电导线及悬垂绝缘子串的相关参数见表1,两跨输电导线跨距分别为l1=260m,l2=200m,初始水平拉力H=25000N,初始条件均相同.根据倾斜角度以及阻尼比的不同组合,将系统的振动响应划分为表2所示的多种不同工况.
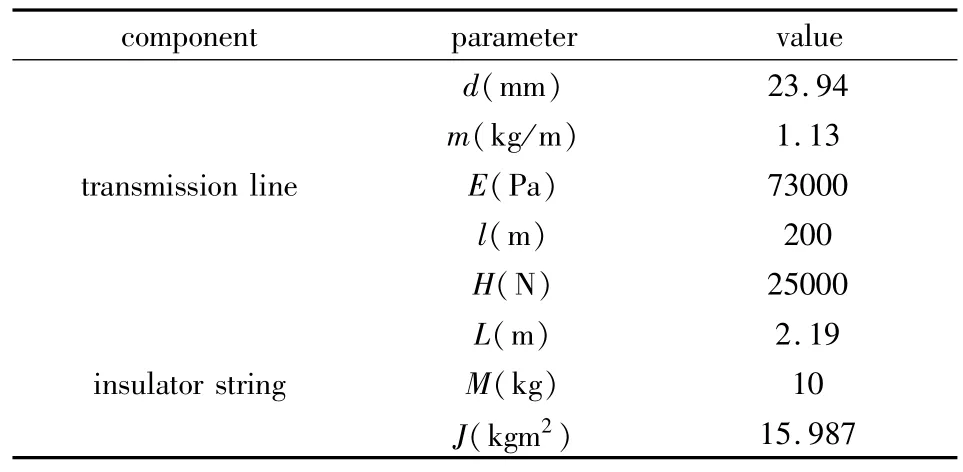
表1 输电导线及悬垂绝缘子串的相关参数Table 1 Parameters oftransmission lines and insulator string
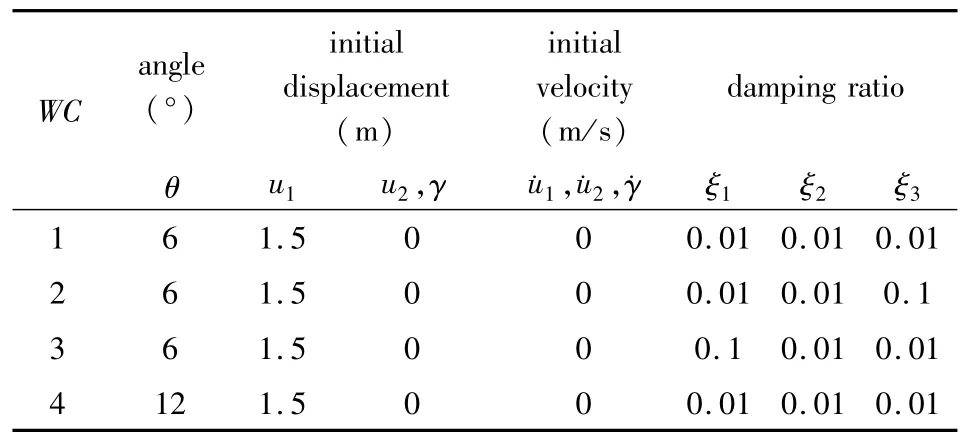
表2 工况划分表Table 2 Classification of analytical cases
将上述参数代入非线性方程组,可计算各种工况下输电导线及绝缘子串振动的位移时程曲线.

图3 输电导线1的位移时程曲线(工况1)Fig.3 Displacement-time curves of transmission line 1(case 1)
图3~图5为系统在工况1下的位移时程曲线.由图可知,在第一档输电导线初始位移为1.5m,第二档输电导线无初始位移的情况下,第二档输电导线的振幅与第一档输电导线的振幅相差不大,这说明了系统在振动过程中,其能量会通过垂悬绝缘子串在两档输电导线间往复传递,由于有阻尼的存在,系统能量逐步减小,最终在200s左右趋于停止.
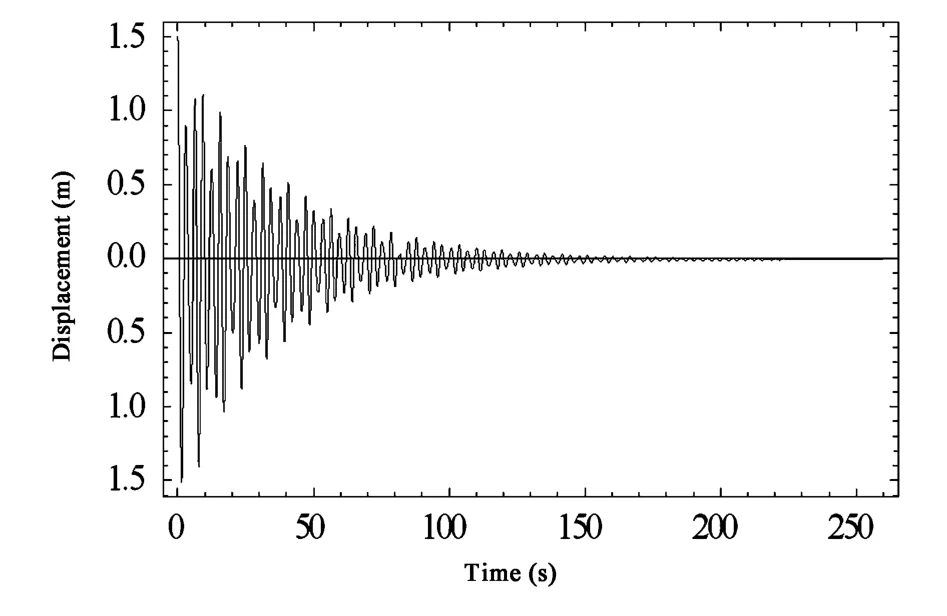
图4 输电导线2的位移时程曲线(工况1)Fig.4 Displacement-time curves of transmission line 2(case 1)
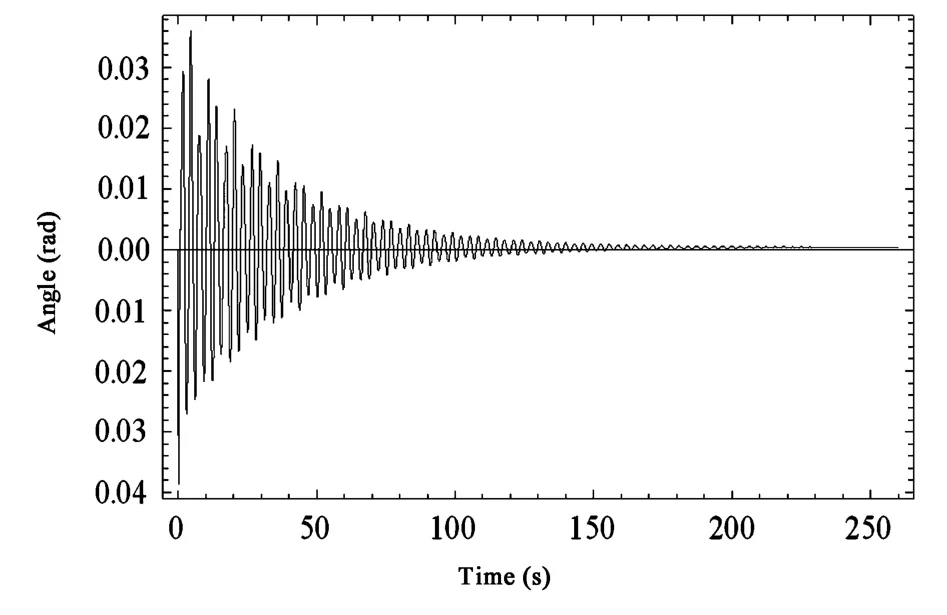
图5 悬垂绝缘子串的位移时程曲线(工况1)Fig.5 Rotation-time curves of insulator string(case 1)
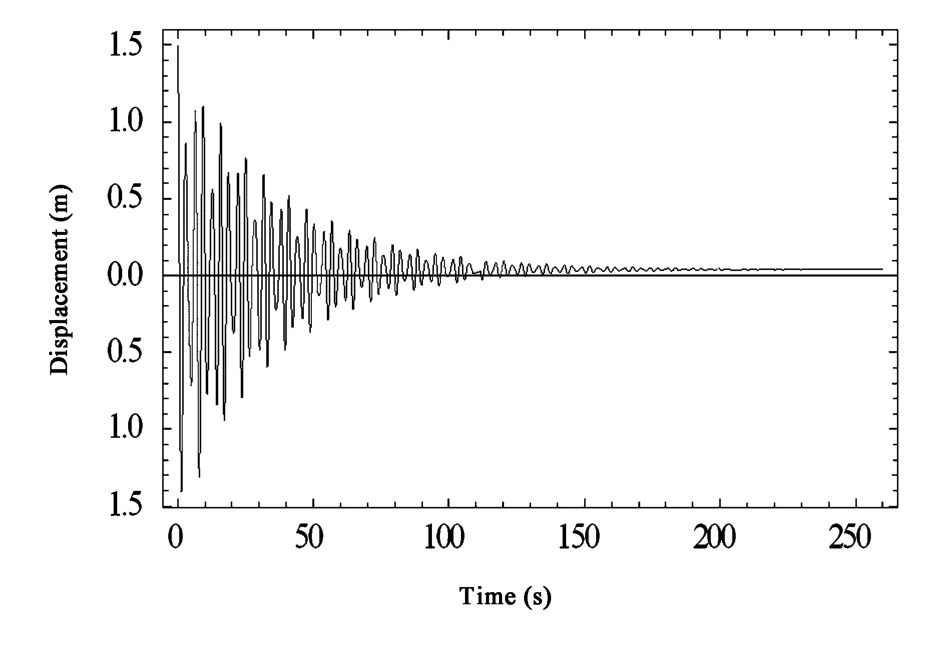
图6 输电导线1的位移时程曲线(工况2)Fig.6 Displacement-time curves of transmission line 1(case 2)
工况2下系统的位移时程曲线如图6~图8所示,与工况1相比,只是将垂悬绝缘子串的阻尼比增大了10倍.
对比工况1与工况2的计算结果可知:将垂悬绝缘子串的阻尼增大10倍后,两档输电导线及垂悬绝缘子串的振幅及衰减时间变化很小,因此,增大绝缘子串的阻尼对抑制输电导线振动的效果并不明显.

图7 输电导线2的位移时程曲线(工况2)Fig.7 Displacement-time curves of transmission line 2(case 2)
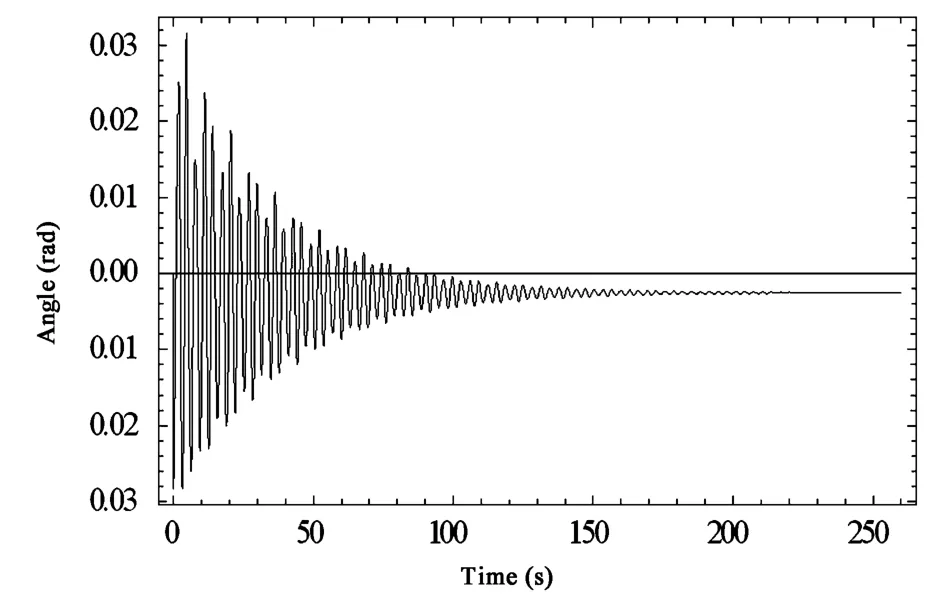
图8 悬垂绝缘子串的位移时程曲线(工况2)Fig.8 Rotation-time curves of insulator string(case2)
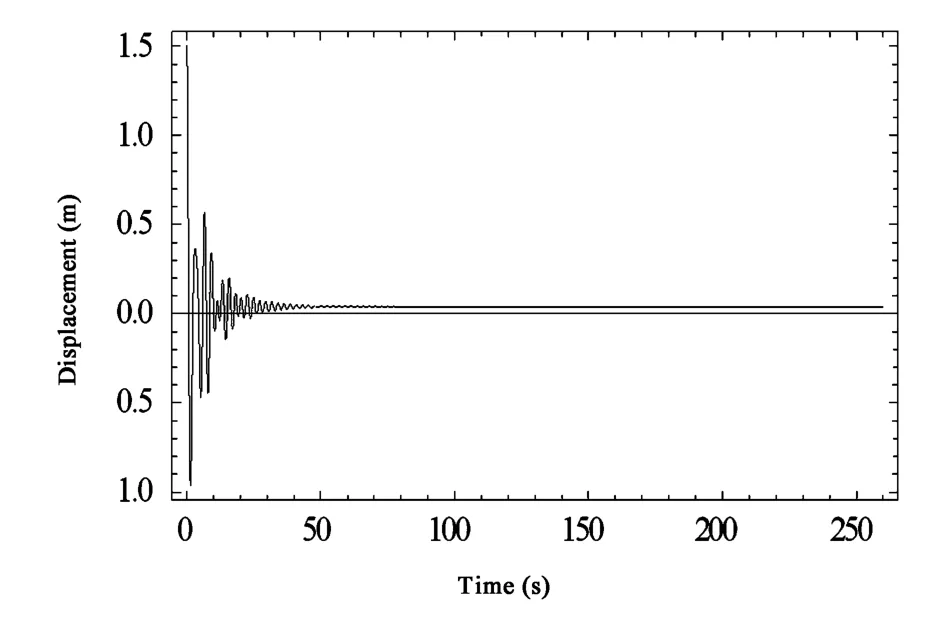
图9 输电导线1的位移时程曲线(工况3)Fig.9 Displacement-time curves of transmission line 1(case 3)
工况3下系统的位移时程曲线如图9~图11所示,与工况1相比,只是将第一档输电导线的阻尼比增大了10倍.
增大第一档输电导线的阻尼,可以显著减小由第一档输电导线通过绝缘子串传给第二档输电导线的能量,而且整个系统的振动也会快速地衰减下来.因此,在输电导线处增加阻尼能取得很好的减振控制效果.
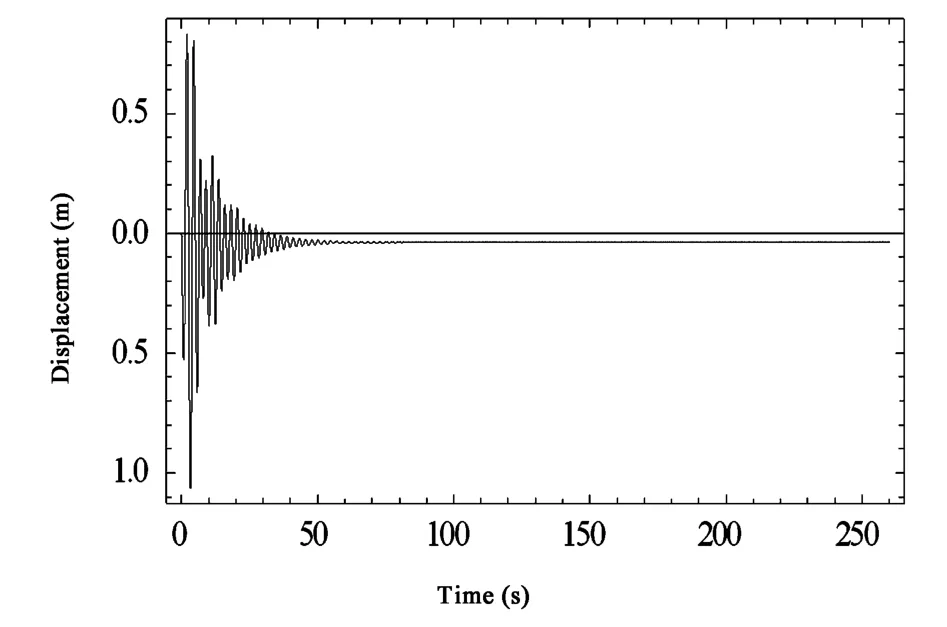
图10 输电导线2的位移时程曲线(工况3)Fig.10 Displacement-time curves of transmission line 2(case 3)
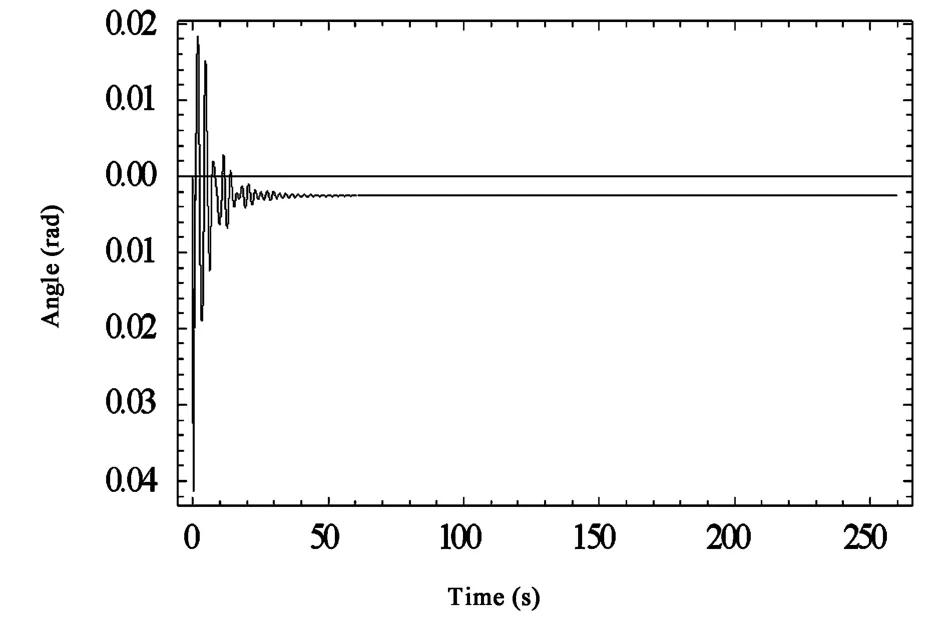
图11 悬垂绝缘子串的位移时程曲线(工况3)Fig.11 Rotation-time curves of insulator string(case 3)
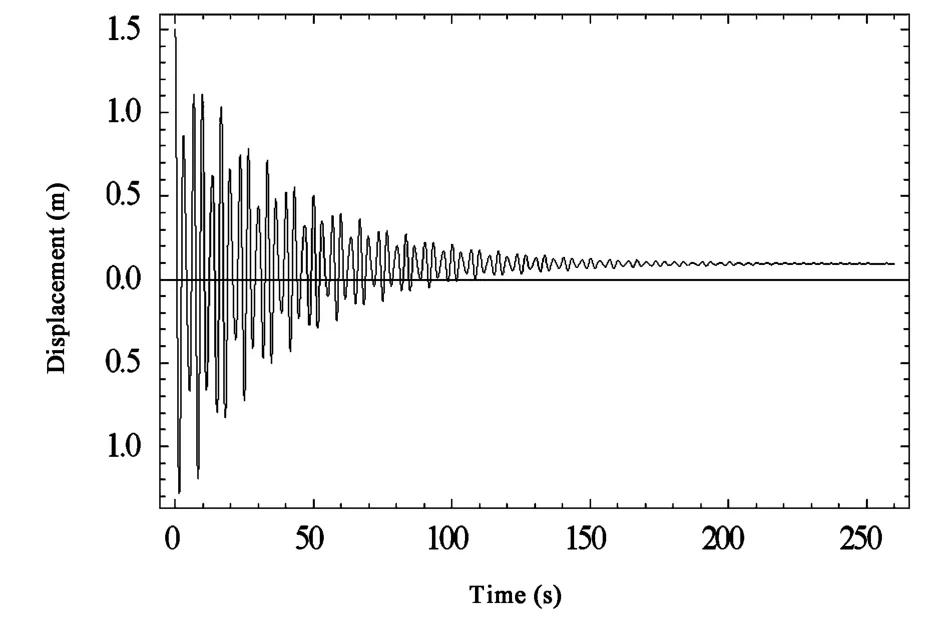
图12 输电导线1的位移时程曲线(工况4)Fig.12 Displacement-time curves of transmission line 1(case 4)
工况4下系统的位移时程曲线如图12~图14所示,与工况1相比,只是将输电导线的传输角度由 6°提高到了 12°.
输电导线的传输角度提高到12°时,两档输电导线的振动幅度并没有明显的变化.但系统的静平衡位置发生了偏移.

图13 输电导线2的位移时程曲线(工况4)Fig.13 Displacement-time curves of transmission line 2(case 4)
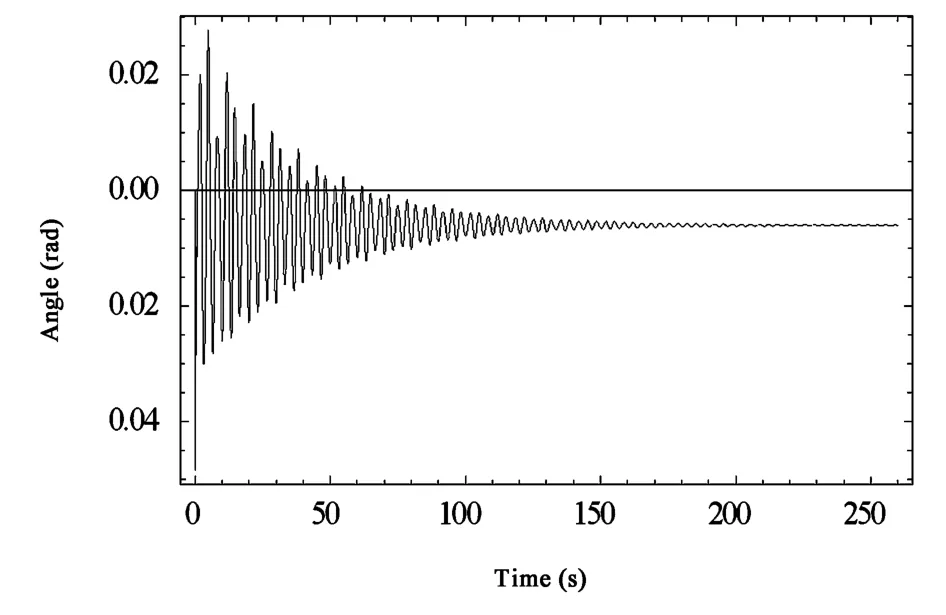
图14 悬垂绝缘子串的位移时程曲线(工况4)Fig.14 Rotation-time curves of insulator string(case4)
2.2 算例2
两档输电导线的跨度分别为l1=400m、l2=380m,传输角度为 6°,初始水平拉力为 H=30960N,其他参数见表1,此时,两档输电导线的频率比接近1∶1.在不考虑系统阻尼,两档导线初始位移均为1.5m的情况下,系统的位移时程曲线见图15~图17.

图15 输电导线1的位移时程曲线Fig.15 Displacement-time curves of transmission line 1

图16 输电导线2的位移时程曲线Fig.16 Displacement-time curves of transmission line 2
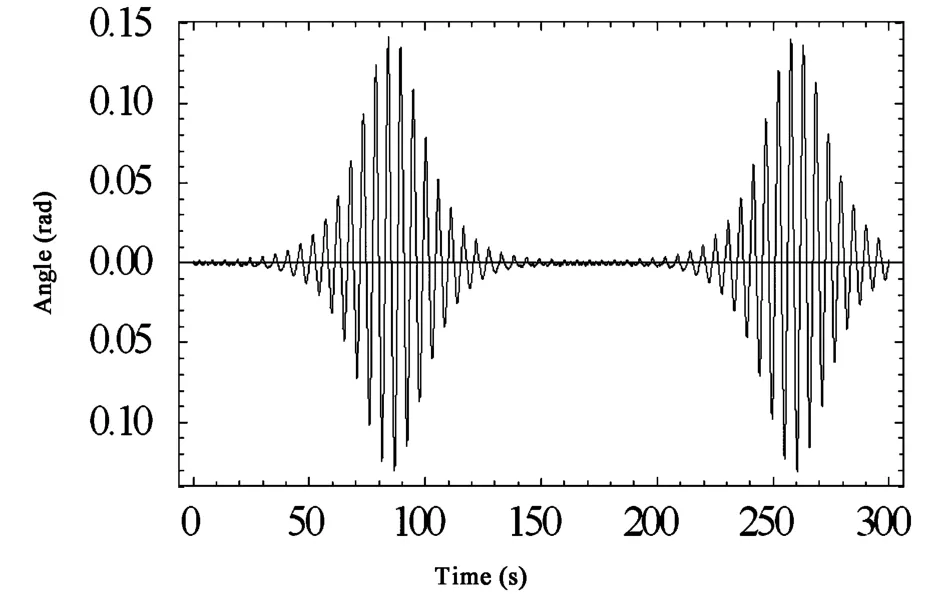
图17 悬垂绝缘子串的位移时程曲线Fig.17 Rotation-time curves of insulator string
显然,系统发生了1∶1共振,两档输电导线和悬垂绝缘子串都出现了拍振现象,它们的振动幅度显著增大.
3 结论
本文建立了连续两档输电导线与悬垂绝缘子串耦合振动的动力学模型及其非线性振动方程,通过对算例的计算分析可得出以下结论:
(1)输电导线振动的能量通过垂悬绝缘子串在相邻两档之间传递,悬垂绝缘子串的耦合作用不容忽略.
(2)在悬垂绝缘子串处增加阻尼,对整个系统的减振效果不明显,但在输电导线处增加阻尼,能起到较好的减振控制效果.
(3)对于有阻尼系统,在小传输角度情况下,传输角度对输电导线的振动幅度没有明显的影响,但系统的静平衡位置会发生偏移.
(4)当两档输电导线的频率比接近1∶1时,系统产生共振,形成了拍振现象,系统的振动幅度有显著增大.
1 刘和云.架空导线覆冰防冰的理论应用.北京:中国铁道出版社,2001(Liu H Y.Overhead conductor ice theory ap-plication of deicing.Beijing:China Railway Press,2001(in Chinese))
2 张仁述.架空电线在悬链状态下的非线性振动响应分析.国防科技大学学报,1987,59(3):1~8(Zhan R S.Response analysis of nonlinear vibration of overhead power line under suspension chain state.Journal of National University of Defense Technology,1987,59(3):1~8(in Chinese))
3 Lin H P,Perkins N C.Free vibration of complex cablemass systems theory and experiment.Journalof Sound and-Vibration,1995,179(1):131~149
4 Bosdogianni A,Olivari D.Wind and rain induced oscillations of cables of stayed bridges.Journal of Wind Engineering and Industrial Aerodynamics,1996,64(2-3):171~185
5 蒋扇英,徐鉴.奇异摄动方法在输电线非线性振动问题中的应用.力学季刊,2009,30(1):33~38(Jiang SY,Xu J.Singular perturbation method and its application in nonlinear systems with fast and slow variables coupling.Chinese Quarterly of Mechanics,2009,30(1):33~38(in Chinese))
6 王昕,楼文娟.多跨输电线路脱冰动力响应研究.工程力学,2011,28(1):226~231(Wang X,Lou W J.Dynamic responseanalysis of multi-span transmission line to ice-sheddingshock.Engineering Mechanics,2011,28(1):226~231(in Chinese))
7 Luongo A,Rega G and Vestroni F.Planar nonlinear free vibration of an elastic cable.International Journal of Nonlinear Mechanics,1984,19(1):39~50
8 李黎,张行,尹鹏.大跨越输电线路脱冰跳跃反应的控制研究.振动与冲击,2008,27(10):61~64(Li L,Zhang X,Yin P.Control for jumping response induced by ice-shedding of transmission lines.Journal of Vibration and Shock,2008,7(10):61~64(in Chinese))
9 赵跃宇,王涛,康厚军,王连华.斜拉桥双索与桥面耦合的非线性参数振动特性分析.湖南大学学报(自然科学版),2008,35(10):1~5(Zhao Y Y,Wang T,Kang H J,Wang L H.Performance study of the nonlinear parametric vibration of coupled bridge decks and two cables.Journal of Hunan University(Natural Sciences),2008,35(10):1~5(in Chinese) )

