多视角生成微专题 全面提升核心素养

成震林 (江苏省灌南高级中学 222500)

在平时教学中，许多数学教师会穿插微专题教学，以重点突破某类问题． 但如果仅仅是将一些难题分类堆积，由教师集中讲解，学生不能有效参与，也不能构建完备的知识体系，这样的微专题教学只能停留在形式上，教学效果并不理想． 微专题的生成不要受内容章节和形式的限制，要打破各种束缚，从多种视角去切入和生成，帮助学生构建完备的知识体系，全面提升学生的数学核心素养． 我校比较重视数学微专题教学，也有多年的实践经验，下面介绍我校常用的几种生成数学微专题的方式．

1 由典型数学结构切入的微专题

此类微专题的定位是高中数学中的基本数学结构． 围绕典型问题，研究这类问题的解题规律和数学结构，在拓展提升中提炼出一般性的数学结构和对应的解决方法． 最后将包含典型数学结构的试题经过改编和变式，打磨成微专题．

此类微专题的教学过程中，教师要引导学生自己去体验，提炼出数学结构和对应的解决方法． 教师要引导学生自己去思考，主动去构建，在探索尝试中寻找解题方法，在抽象概括中提炼数学结构． 这些数学结构和对应的解决方法不要直接告诉学生，因为空洞的说教，没有学生自己真切的体验，教学效果甚微．

案例1基本不等式应用——多元问题

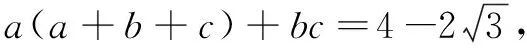
例2已知实数a,b,c满足a+b+c=0，a2+b2+c2=1，则a的最大值是．

变式 已知实数x,y,z，满足x+y+z=1，x2+y2+z2=3，则z的最大值为．

例3已知实数a,b,c满足a+b+c=9，ab+bc+ca=24，则b的取值范围是．

变式 已知实数a,b,c满足a+b+c=9，ab+bc+ca=24，则abc的取值范围是．

巩固练习：1.已知x,y,z均为正数，xyz(x+y+z)=1，求证：(x+y)(y+z)≥2.

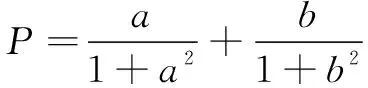
设计意图章建跃认为，数学思想方法是具有普适意义的、迁移能力强的根本大法[1] 594，所以要让学生在掌握数学结构和感悟数学思想中提升数学核心素养． 本微专题以变式题组的形式出现，围绕多元问题处理的主要方向——减元，以一条主线将这些题组联系起来． 学生需要对这一数学结构有清晰的认识和整体的把握，才能灵活运用，所以要由浅入深，层层推进，让学生掌握数学结构和对应的处理方法，并感悟其中的数学思想．

小结此微专题是本人高三教学中的一节公开课所用材料． 对于数学中的典型结构，有时学生缺乏深刻的认识，更不能灵活运用到综合题的解题中去，所以要抓住这些典型的数学结构去切入和生成微专题． 围绕数学中的典型结构去生成微专题是我校数学微专题教学中经常采用的形式，我校在高三教学和高一、高二的阶段性复习教学中，都会穿插此类微专题的教学．

2 由高频考点切入的微专题

为了全面提升学生的核心素养，可以由高考题中的高频考点切入，打磨成实用性和个性化的微专题． 高考题中的高频考点往往折射出高中数学的核心知识，通过此类微专题的针对性训练，使学生掌握高中数学的基本思想和方法． 在教学中要让学生自己去体验和感悟基本数学思想和方法，形成自己的知识经验结构，并转化为自己的经验和习惯，学生才能真正掌握[2]192．

案例2导数应用——不等式恒成立问题

(一)高考真题重现

1.已知函数f(x)=ex+e-x，其中e是自然对数的底数.

(1)证明：f(x)是R上的偶函数；

(2)若关于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立，求实数m的取值范围；

2.已知函数f(x)=ax+bx(a>0,b>0,a≠1,b≠1).

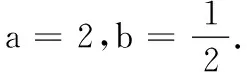
(2)若01，函数g(x)=f(x)-2有且只有一个零点，求ab的值．

(二)典型例题

(1)若函数f(x)的图象在x=0处的切线与直线x+y=0垂直,求a的值；

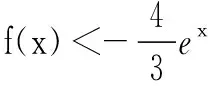
(1)当a=2时,求出函数f(x)的单调区间；

(2)若不等式f(x)≥a对于x>0的一切值恒成立，求实数a的取值范围．

3.已知函数f(x)=ex-e-x-2x.

(1)求出函数f(x)的单调区间;

(2)若不等式f(2x)-4bf(x)>0对于x>0的一切值恒成立，求实数b的取值范围．

4.已知函数f(x)=ax2-a-lnx，其中a∈R.

(1)讨论函数f(x)的单调性;

(1)求证:函数y=f(x)在区间(1,e)上存在最大值;

设计意图此微专题是我校一位骨干教师的高三公开课材料，课后本人和他就此微专题的生成视角和方法作了深入的交流． 此微专题生成的视角是高频考点——不等式恒成立问题． 处理不等式恒成立问题的主要方法是构造函数，在构造函数时有直接构造和分离参数两种主要途径，围绕这两种方法去打磨题组，通过不同背景的问题让学生体验解题路径选择的重要性，并提高学生陌生环境下对这一基本方法的灵活运用能力和数学素养．

小结高频考点往往是高中数学的主干，是考查学生数学素养的重要载体． 围绕高频考点去切入和生成微专题具有较强的教学实效性，所以受到我校教师的特别青睐． 在阶段性复习中，对于相同或相近的高频考点，可将它们按照一定的主线去生成微专题，突出其中的数学思想和数学方法，培养学生的数学核心素养．

3 由知识体系切入的微专题

数学的严谨性、抽象性的学科特点，使得数学教学中强调系统化策略更显重要． 系统化、结构化的知识迁移能力强，在新的认知活动中能发挥积极、有效的作用[2]180． 此类微专题生成的视角要跨越章节界限，按照一条主线将零散的知识按照内部的逻辑整合起来，让学生参与知识体系的建构过程． 学生只有经历了对知识的深加工过程，做到知识的结构化、自动化和策略化，才能有效地用来创造性地解决问题[2]91．

案例3一道课本习题的研究与拓展

问题1已知圆C的方程为x2+y2=r2，求经过圆上一点M(x0,y0)的切线的方程. (苏教版必修2第105-107页)

变式1 已知圆C的方程为(x-a)2+(y-b)2=r2，求经过圆上一点M(x0,y0)的切线方程.

变式2 已知圆C方程为x2+y2+Dx+Ey+F=0，求经过圆上一点M(x0,y0)的切线方程.

问题2比较切线方程与原方程，形式上有什么变化规律？

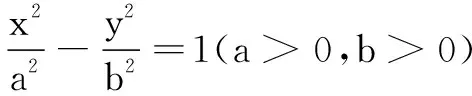
过抛物线y2=2px(p>0)上一点M(x0,y0)的切线方程为.

变式3 已知圆C的方程为x2+y2=r2，若M(x0,y0)为圆外一点，会有怎样的结论？

变式4 已知圆C的方程为x2+y2=r2，若M(x0,y0)为圆内一点，过点M(x0,y0)作动弦AB,过A，B分别作圆的切线，设两条切线的交点为P，求证：点P恒在一条定直线上运动.

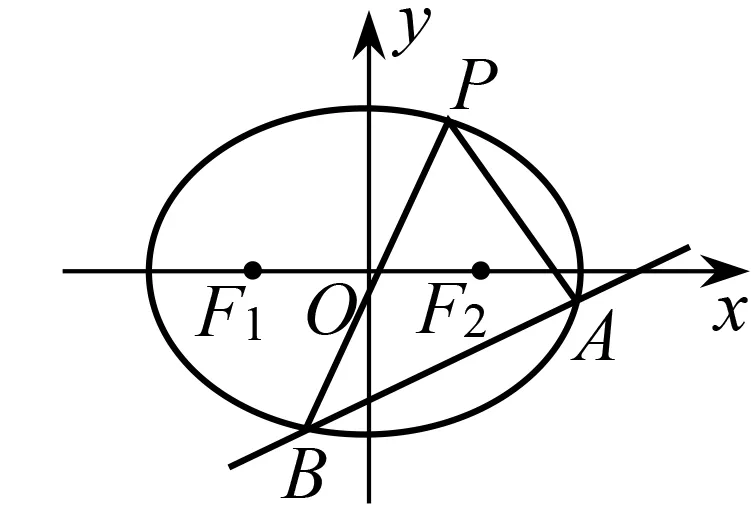
图1

链接3 已知两条直线a1x+b1y+1=0和a2x+b2y+1=0都过点A(1,2)，求过两点P1(a1,b1),P2(a2,b2)的直线的方程. (苏教版必修2第77页)

链接4 已知圆C的方程为x2+y2=r2，直线l:ax+by=r2.

(1)当点P(a,b)在圆C上时，l与C具有怎样的位置关系？

(2)当点P(a,b)在圆C外时，l与C具有怎样的位置关系?(苏教版必修2第106页)

设计意图此微专题是我县名师领航团队活动中我校一位教师上的公开课材料． 我校数学教师平时注意对知识的拓展和提升，将可以组块的知识通过一条主线联系整合起来． 因为数学能力是在获得数学知识、数学技能的基础上，通过广泛迁移，不断概括化、系统化，即类化而实现的[2]219，此类微专题承载着健全学生知识体系和提升学生数学核心素养的功能．

小结在我校数学探究性学习或者高三一轮复习中，此类微专题很有用武之地． 围绕知识体系生成的微专题，可以通过相近知识的类比和联系形成知识体系． 由此视角生成的微专题让学生站在系统的高度去掌握和运用知识，帮助学生挖掘知识之间的内在联系，使学生建立清晰、稳定、可辨别的、迁移能力强的“数学知识结构图”． 使学生不仅理解知识及其蕴含的数学思想方法，而且懂得知识间的逻辑关系、联系方式[1]733．

4 由易错点切入的微专题

要全面提升学生的数学素养，针对学生的易错点进行补救也是行之有效的办法． 学生的错误可能是由概念理解的偏差或者不良的思维习惯所导致的，也可能是对数学的本质缺乏深刻的理解．

通过课堂对话、批改作业、学生板演、个别辅导等多种形式进行师生交流，找出学生知识的漏洞和思维的偏差，从而针对性地设置个性化的微专题． 例如，学生三角函数中的某类题目没做好，找出学生没做好的原因，如对诱导公式的连续使用不熟悉，就可以设计一个“诱导公式连续使用”的微专题． 又如，学生对解析几何计算方法的选择和优化意识不强，可以针对性地生成一个“解析几何计算方法的选择和优化”的微专题．

小结查漏补缺是教学中的常见术语，但在数学教学中如何科学有效地落实，由易错点切入的微专题是非常有效的办法． 我校数学教研组非常重视此类微专题的收集、整理和优化，在适当的时机穿插使用，对于优化学生的知识结构发挥了重要作用．

以上几种微专题生成的视角虽然不同，但它们都是我校数学教学中生成的实用性强且具有个性化的微专题的重要方法． 多视角生成微专题是传统教学的突破和创新，是对重难点内容的强化和提升，更是我校在全面提升学生数学核心素养方面的积极探索．