基于算法视角的解析几何例题教学——椭圆中一类非对称问题的处理策略*

张文海 (江苏省苏州实验中学 215011)

《普通高中数学课程标准(2017年版)》明确了“数学运算”的定位:“数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养. 主要包括：理解运算对象，掌握运算法则，探究运算思路，选择运算方法，设计运算程序，求得运算结果. ”“通过高中数学课程的学习，学生能进一步发展数学能力；有效借助运算方法解决实际问题；通过运算促进数学思维发展，形成规范化思考问题的品质，养成一丝不苟、严谨求实的科学精神. ”

解析几何是高中数学的重点内容，也是考查学生数学运算素养的重要载体之一． 要正确解答圆锥曲线的综合问题，除了要具有较强的计算能力，还需要多一些思考，通过对条件及图形的分析，合理设参，确定解题方向，规划解题路线，往往能起到简化运算的效果．

图1

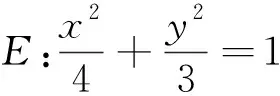
1 明确运算对象，探究运算思路

例题教学首先应带领学生一起认真阅读题目，理解题意，把要解决的问题作为研究对象，对它进行深入而全面的分析，找出题目直接表达出来的显性条件和经过思考分析合理转化而来的隐性条件，探寻条件与结论的联结点，确定运算思路． 在此基础上还需要制定解题计划，初步预设解题的各个环节：求解这个问题的第一步做什么？第二步做什么？解决问题的关键是哪一步？哪一步运算量可能有点大?如此等等，做到心中有数．

策略1 直接求根，代入化简

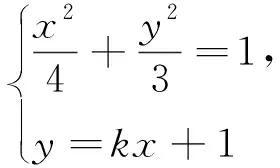
策略2 瞄准减元，一减到底

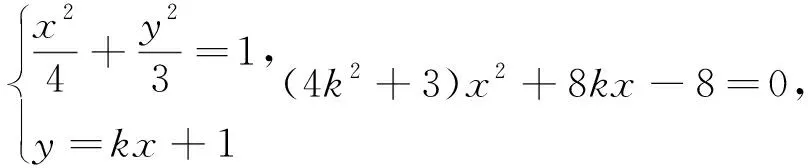
评析 在得到kx1x2+(2k+2)x1+(4k-1)x2+6=0 ①后，抓住x1，x2是方程的两个根，故可以通过根与系数的关系得到x1+x2，x1x2与k的关系，从结构上去构造x1+x2，x1x2进行整体代换. 由于是非对称关系，所以不能完全用根与系数的关系式进行彻底的消元，需要再结合求根法进行处理. 这种处理方法先从整体结构上进行把握，对于局部的地方再进行个性化的处理，有助于优化解题过程，提高解题速度.

2 辨析式子结构，选择运算方法

数学运算常常包括“数”的运算和“式”的运算. 对于“数”的运算，学生从小到大、从数学到生活随处可见，无形之中锻炼了运算的能力；而对于“式”的运算，平时接触不多，加上参数之多，学生普遍感到棘手. 解析几何的本质是用代数的方法解决几何问题，因而解析几何题离不开代数运算，这就使得运算能力不强的学生害怕繁难的运算. 在解题教学中教师如能多加强运算指导，还是能逐步提高学生运算能力的． 其次，要加强“算理”分析，就是分析运算规则，并形成合理的“算法”思维． 如帮助学生分析代数式子的结构特征，展示式子变形中的结构意识，强化观察运算方向的自觉性，强化关注运算结构的简洁性，选择合适的运算方法.

策略3 瞄准减元，一减到底

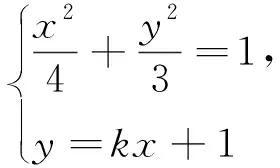
策略4 设斜求点，抓住共线

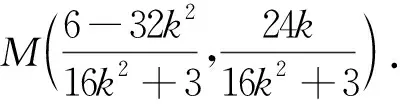
评析 遇到斜率问题时，可以先设出点的坐标，再表示斜率；亦可先设出直线的斜率，求出点的坐标，再根据条件处理. 两种设法的不同之处在于，第一种设法斜率表示简洁，但参数较多，消参不易；第二种设法参数较少，但运算量大. 在设出直线AM，BN的直线后，先把它们和椭圆联立求出点M，N坐标，再根据M，N，C三点共线，建立关于k的方程，通过解方程即可得解.

3 理清问题本质，提升数学思维

在课堂教学中，教师应结合具体的数学问题，引导学生如何抓住问题中的“变”与“不变”的规律，以“不变”来应“万变”，直达数学问题的本质，使学生从数学题海中跳出来，站在更高的角度去看待问题、思考问题，从而达到提升学生分析、解决问题的能力，提升学生的数学思维能力的目的.

策略5 转化位置，巧用公式

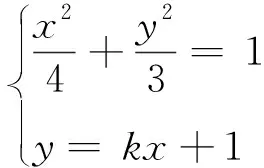
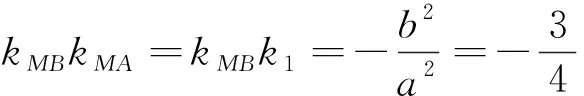
4 教学反思

《普通高中数学课程标准(2017年版)》明确提出要注重培养学生的数据分析和数学运算素养，而解析几何是落实这两个素养最好的载体之一. 因此，在解析几何教学中不仅要重视几何问题代数化的思路分析，而且要重视解题过程中运算的分析指导，对其中如何运算以及如何优化运算进行重点剖析，突破学生思维中的障碍节点，解决学生在解析几何中常见的思路易得、运算受阻的主要问题，使学生的运算素养得到真正的提升．

(1)选择合适的例题，暴露思维的障碍

例题教学的主要任务是使学生通过具体例题的学习巩固数学基础知识，掌握数学基本技能，在问题的分析和解决中形成自己的基本活动经验，从而提升自己的数学能力. 好的例题可以唤起学生对旧知识的回忆，促进对原有知识的沟通联系，调整学生头脑中原有知识的逻辑关系，借以开阔学生思路，促使学生思维向多向发散． 因此，例题的选择要注重基础性、针对性、思想性和拓展性，应有利于学生在易错处、困惑处顿悟，在常规与平实中暴露学生的思维障碍，在不断纠错和调整中促进学生思维能力的发展．

(2)重算法算理分析，优化运算的路径

算理是指计算的原理和依据，即为什么这样算；算法指计算的基本程序和方法，即怎样算. 算理是算法的基础，算法则是算理的抽象，因此教学中要做到算理和算法并重，使理解算理和掌握算法相互作用、共同促进. 由于一些教师对解析几何的认识定位不准，平时的教学重思路分析、轻运算指导，或将其仅仅等同于运算技能，往往只将注意力集中在对运算技巧的训练上而缺少对算法背后隐藏算理的揭示，导致学生知其然而不知其所以然． 案例研究表明，清晰的算法思想和对运算过程的预判、调整是提高解析几何解答题运算求解能力的根本． 如果我们能从算法的角度预设几个解题方案，先预判解法的优劣，再确定解题方案，长此以往，就能在解决一道题的同时发散学生的思维，学生对题目的认识就会更深刻． 坚持从算法的角度思考问题，养成良好的思考习惯和认知习惯，定能厚积薄发．

(3)建构自己的理解，促进素养的内化

解析几何中不同的解题路径会产生解决问题的难与易、解题过程繁与简的差距，而学生受自身思维的制约，往往不能灵活运用已有的知识和解题经验对新的问题进行巧妙的处理，从而产生复杂的运算操作，最终半途而废，导致解题失败，久而久之对解析几何失去信心. 因此，教师要基于学生的学情选择恰当的例题，对学生进行代数式观察、运算方向监控、运算长度预估等多重的思维训练，探索降低运算复杂度的方法和技巧，让学生建构自己的理解，并激发出学生思考的热情. 在这样的过程中，学生的思维品质和数学运算素养都将得到相应的提升．

总之，我们只有在解析几何的教学中让学生多实践、多反思、多总结，方能以简驭繁，事半功倍. 数学运算能力的提高不是一蹴而就的，而是一个渐进的、螺旋式上升的过程. 我们的教学站位要高、措施要细、训练要实，使解题建构在高层次的思维面上，让教学的每一步都能引导学生逐步提高数学运算素养.