面向多椭圆曲线的高速标量乘法器设计与实现

于斌，黄海，刘志伟，赵石磊，那宁

（哈尔滨理工大学软件与微电子学院，黑龙江 哈尔滨 150080）

1 引言

随着处理器算力的不断增强，传统加密算法的安全性正受到日益严峻的考验，需要更加复杂的加密算法来保证数据的安全。椭圆曲线加密算法是近年来比较活跃的一种非对称加密算法，与对称加密算法中的高加密标准（AES,advanced encryption standard）一样在密码系统中得到广泛使用[1]。在最新的传输层安全性协议1.3 版（TLS1.3,transport layer security protocol version 1.3）中，使用多种椭圆曲线进行数据加密，无论是在数量上还是在实际使用频率上，都凸显了椭圆曲线加密日益重要的位置[2]。

椭圆曲线的运算速度和对多种曲线的兼容一直是研究的重点。Kudithi 等[3]利用可编程逻辑器件（FPGA,field programmable gate array）完成了适用于物联网的加密算法结构，利用较低面积完成了对P224 和P256 椭圆曲线的支持；Hossain 等[4]设计了同时适用于专用集成电路和FPGA 的标量乘操作步骤，同样支持了2 条曲线；Liu 等[5]优化了非相邻形式（NAF,non-adjacent-form）算法并完成了P256 位的标量乘设计；Lee 等[6]采用双处理单元改进了自右向左的标量乘算法；Chung 等[7]改进了蒙哥马利模乘的流水结构，提升了标量乘的整体速度。

本文设计了椭圆曲线硬件加密中使用的一种标量乘法器，选取最常用的Curve25519 和secp256r12曲线，使其尽可能复用乘法单元完成标量乘，使用了256 位乘法器得到乘法结果并采用快速模约简来达到提高模乘速度的目的。此外，考虑标量乘的使用环境，尤其是在签名和验签中的使用情况，本文设置了对于基点和普通点不同的算法，同时支持多标量乘，使设计的标量乘法器能够满足椭圆加密的各种应用需求。

2 研究背景

椭圆曲线有很多分类，使用较早的一类曲线是Weierstrass 曲线，满足式(1)所示的曲线方程。

TLS1.3 所选用由美国国家标准与技术研究所（NIST,National Institute of Standards and Technology）提出的secp256r1、secp384r1 和secp521r1 这3 条曲线，就属于Weierstrass 曲线。

椭圆曲线上的运算采用模运算，包括模加减、模乘和模逆运算，最核心的运算方式为模乘和模逆。点加和倍点运算以模运算为基础，并进一步用来实现标量乘。标量乘的性能也是衡量椭圆曲线加密性能的一个重要的指标，为了得到更快的加密速度，需要尽可能快速地完成标量乘。根据标量乘的运算过程，大致可把提高标量乘速度的优化方法分为3 类：优化标量乘算法[8-13]、转换坐标系[14-16]和优化模运算算法[17-20]。

第一类优化方法是改变标量乘kP的运算过程，降低总体运算量，其中，P是椭圆曲线上的点，k是待乘的倍数。优化的方法包括：使用自左向右和自右向左2 种算法，对于n位的k值需要计算n次倍点和次点加，其中自左向右算法的点加和倍点可以并行运算，但是需要额外的模运算单元[8]；把k做相对简单的预处理，实现NAF 算法，把点加的次数降低为次[9]；对k做m位的分段处理，实现窗口NAF 法，预计算需要计算窗口内的2m个点运算结果，预计算量较大[10]；使用Comb 算法来快速完成标量乘，但需要的预计算量庞大[11]；采取适用于多标量乘的Shamir 算法，用一次标量乘的时间完成2 个标量乘的相加[12]；采用多基链算法，增加三倍点、五倍点形成多基链来加速标量乘[13]。

第二类方法采用转换坐标系，目的是优化标量乘中的点加和倍点运算。原曲线方程使用二元坐标系，点加运算需要一次模逆和3 次模乘（模平方记为模乘，忽略模加减运算，下文相同），倍点运算需要一次模逆和4 次模乘，而模逆运算需要消耗大量时钟周期，因此可以通过坐标系的转换改变点加和倍点运算计算式，消除模逆运算，例如射影坐标系，把坐标(x,y)按转换式转换为(X,Y,Z)，点加运算需要14 次模乘，倍点运算需要12 次模乘[14]。雅可比坐标系使用比较普遍，转换式为这需要16次模乘来完成点加运算，10次模乘完成倍点运算[15]。此外还有修正的雅可比坐标系[16]、混合坐标系[16]等变换，其目的都是在开始时做一次变换，随后在计算点加和倍点过程中消除模逆运算，最后的计算结果再转换为二元坐标，整个标量乘只使用一次模逆运算。

第三类优化方法是从基本的模运算入手，提高模运算的速度，主要是模乘和模逆运算。模乘运算使用较多的是蒙哥马利模乘算法，通过将多位的模乘分解为2m位的模乘，利用二进制的特点，进行多次迭代运算得到最后的模乘结果[17]。IEEE 给出对于NIST 中所使用的模p快速约简公式，把2 个数据的乘法结果直接做快速的模约简，得到模乘结果[18]。模逆运算的计算式一般会采用费马小定理，如式(2)所示。

通过简单整理即可得到模逆运算的计算式为

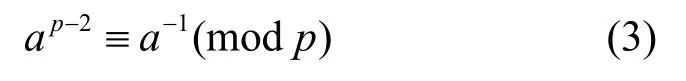
这样可以不需要模逆运算，只需要使用模乘即可完成模逆运算，也可以采用专门的模逆模块来完成模逆运算。蒙哥马利模逆算法与蒙哥马利模乘配合使用，不需要经过转换也可以完成模逆运算[19]，也可以使用二进制右移算法，通过多次简单比较和加减来计算模逆运算，资源开销较小[20]，独立设计模逆运算主要是为了释放模乘单元，达到并行的目的，同时减少计算周期数。

还有一类椭圆曲线是蒙哥马利曲线，其方程为

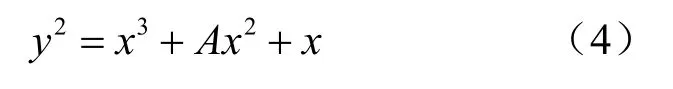
Curve25519 曲线属于蒙哥马利曲线，由Bernstein[21]于 2005 年提出，并在 2016 年与Curve448 一起成为国际标准[22]，这2 种曲线也被TLS1.3 采用。此类曲线提出较晚，在近年开始得到广泛使用，其标量乘本身具有抗SPA（simple power analysis）特性，所以一般直接使用蒙哥马利阶梯算法而不会做修改[23]，只是在模乘部分做优化，Düll等[24]计算给出了标量乘所需的模乘和模平方数。

上述算法虽各有优点，但都是仅考虑单一使用而优化的。在椭圆曲线加密中，标量乘有很多使用场合，涉及基点G或者普通点P的标量乘，在验签时需要计算多标量乘λP+μG，同时服务器端签名验签频繁，对标量乘速度的要求极高，需要一个能在各种使用场合下都具备较高性能的标量乘法器。

本文全面考虑标量乘法器在椭圆加密算法中的使用情况，完成了如下工作。

1) 选择适用于不同情况的标量乘算法，使标量乘计算普通点P、基点G和多标量乘λP+μG时都达到较快的运算速度。

2) 推导了Curve25519 的快速模约简公式，结合已有的secp256r1 的快速模约简公式，用快速模约简实现模乘。

3) 结合利用模约简计算模乘的运算特点，排布了secp256r1 和Curve25519 这2 条曲线的点加倍点操作步骤，根据Comb 算法特点简化点加操作，并排布了雅可比坐标系下特殊点加（有一个点的Z值为1 时）的操作步骤。

4) 在保证模乘速度的前提下，设计充分考虑复用以降低面积，完成适用于secp256r1和Curve25519曲线的标量乘法器。

3 标量乘法器设计

标量乘法器的设计也同优化一样，需要完成标量乘算法的设计、点加倍点的设计和模运算的设计。在实际使用情况中，secp256r1 曲线和Curve25519 曲线使用频繁且具有相近的位数，故将这2 条曲线的标量乘集成为一个单元进行设计。由于采用了3 种标量乘算法来适应不同需求，整个设计采用了3 个独立的子控制模块来实现不同算法的控制功能，在工程中可以根据不同的使用场合来切换算法，调用运算单元，达到最快的速度。标量乘法器的整体结构如图1 所示。

图1 标量乘法器的整体结构

运算单元完成所有点加倍点运算，除必需的控制逻辑之外，主要运算部分是一个256 位的乘法器，通过快速模约简单元完成模乘功能，所有预计算数值和中间计算结果都存储至临时寄存器堆中，最大限度地复用了硬件资源。由于标量乘计算结果需使用模逆运算转换至二元坐标系，考虑到椭圆加密的运算过程，将模逆端口一并引出，可供外部调用，使整个设计可以满足椭圆加密中所有关键步骤的使用需求。

3.1 标量乘算法

使用secp256r1 曲线时，加密系统会在签名和公钥生成时使用基点G的标量乘，在密钥交换时使用普通点P的标量乘，在验签时使用λP+μG的多标量乘，所以选择了Comb 算法和Shamir 算法来应对不同使用场合。算法1 为编码长度为4 的Comb算法[11]。

算法1编码长度为4 的Comb 算法

输入256 位二进制数λ={λ255λ254λ253…λ1λ0}和椭圆曲线secp256r1 的基点G。

输出标量乘Q=λG

Comb 算法需要的预计算量非常大，例如{1111}G就需要计算(2192+2128+264+20)G，在计算普通点时该算法并不占优势。但是由于基点G已知，Comb 算法的预计算表可以提前完成并存储，这样在计算时直接使用该表，再使用64 次倍点和最多64 次点加即可完成基点G的标量乘，需要额外付出的代价是15 个点坐标的存储阵列，其中，{0000}G不需要存储。

Shamir 算法可以计算λP+μG的多标量乘，经过预计算后可以用一次标量乘的时间完成λP+μG的计算。算法2 为窗口为2 的Shamir 算法[12]。

算法2窗口为2 的Shamir 算法

输入256位二进制数λ={λ255λ254λ253…λ1λ0}，μ={μ255μ254μ253…μ1μ0}，椭圆曲线secp256r1上的普通点P和基点G。

输出Q=λP+μG

当λμ≠0 时，对于输入的P、G点坐标，需要3 次倍点和4 次点加来计算预计算表，预计算结束后进入循环，4 倍点不设置专用的计算式，复用倍点计算式2 次来完成4 倍点功能，这样可与Comb 算法复用倍点运算单元，所以在窗口为2 的Shamir 算法中，依然会计算256 次倍点和最多128 次点加，同时存储除了(00)P+(00)G之外的15 个点坐标。如果只算普通点乘的λP，则令μ=0 即可，此时进行一次点加和倍点即可完成预计算，标量乘循环计算时所需次数与λμ≠0 时相同。

对于Curve25519 曲线采用蒙哥马利阶梯算法来完成标量乘，维持抗SPA 特性，其算法步骤如算法3 所示[23]。

算法3Curve25519 标量乘算法

输入255 位二进制数k，点坐标P1=(x1,y1)的横坐标x1

输出标量乘结果kP1=(x2,y2)的横坐标x2

其中，cswap 操作是根据swap 的值来交换2 个输入的坐标值，算法不单独列出；阶梯算法Ladder step在3.2 节中给出详细步骤。

3.2 高速点加和倍点运算设计

运算单元的功能是执行点加和倍点运算，按2 条曲线划分，执行的计算式不同。对于椭圆曲线secp256r1，采用的标量乘算法中点加操作相对较少，故采用倍点较快的雅可比坐标系，倍点计算式[16]为

由于采用快速模约简进行模乘，模乘结果需要经过一个周期的乘法和一个周期的模约简才可以被继续使用，为减少模乘次数，并结合式(5)，将倍点运算的操作步骤排布如表1 所示，共需9 个周期完成倍点运算(X3,Y3,Z3)=2(X1,Y1,Z1)。

表1 倍点运算步骤

表1 的步骤5 中，t5得到2S，t1得到M，步骤7的X3即为T值，其余各值依次代入即可验证是否与式(5)一致。为了保证数据的有效性，模乘结果需间隔一周期才能作为输入，例如步骤2 的乘法结果t2需在步骤3 进行模约简，在步骤4 得到模乘结果并继续参与计算，模约简过程并未列在算法中。模加减单元作了特殊设计，增加了3 倍模加、被减数为1.5 倍的模减，保证乘法器的连续使用并减少模乘的次数。同时考虑256 位乘法的时间时延较大，而模约简的时间时延相对较小，所以在模约简之后可以安排一次模加减，进一步压缩操作步骤，如步骤2 中t1的使用就是如此。表1、表2 和表3 均采用同样的设计思路排布，模运算具体内容见3.3 节。

正常情况下表1 的倍点运算需要8 个周期模乘加一个周期的约简等待，但倍点运算后立即会进行点加或者倍点运算，所以通过调整(X,Y,Z)的输出顺序，可以在下次乘法操作同时进行模约简，实际工作中需要8 个周期可完成一次倍点运算。

对于点加公式，需要做分类处理以达到最优化，在Shamir 算法中需构造预计算表，但是表内数据都是在计算开始后得到的，所以都是普通的三元坐标(X,Y,Z)，按式(6)排布操作步骤如表2 所示，共需 17 个周期完成普通点加运算(X3,Y3,Z3)=(X1,Y1,Z1)+(X2,Y2,Z2)。

表2 中步骤3 计算U2，步骤4 计算U1，步骤5的t4计算H，步骤8 计算S2，步骤9 计算S1，步骤11的t3计算r，依次代入后，X3可得

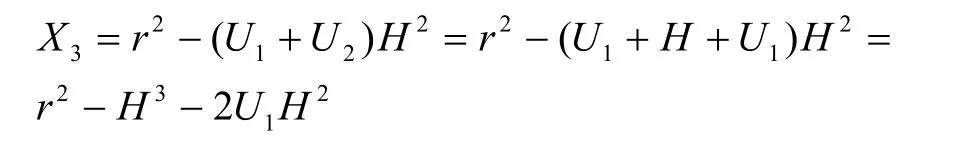
表2 普通点加运算步骤

步骤16 中的Y3可得

步骤17 中对Y3做0.5 倍模加，Z3代入即可，所得结果与式(6)一致。

在Comb 算法中，由于每次点加的αiG都是预先计算并存储的，其点坐标格式均为(X,Y,1)，Z=1不需要存储，且可以将式(6)做进一步优化和整理，并按照时序排布操作步骤如表4 所示，共需13 个周期可完成一次特殊点加运算(X3,Y3,Z3)=(X1,Y1,Z1)+(X2,Y2,1)。

表4 与表2 相似，依次代入后即可验证是否与式(6)一致。点加运算结束后会立刻进行倍点运算，所以在2 种点加运算的操作步骤上都对最后输出的坐标做了调整，以适应点加倍点的连续运算，最后一步的模加减均与下一运算的乘法同时运行，让乘法器使用率达到最高。

Curve25519 的点加和倍点是采用阶梯算法一起完成的，按RFC7748 中的参考算法，将操作步骤重新排布如表3 所示，共需12 个周期完成操作，可根据输入的(X1,X2,Z2,X3,Z3)计算得到(X2,Z2,X3,Z3)。

表3 Ladder step 阶梯运算步骤

表4 特殊点加运算步骤

这样，根据曲线和算法来调用不同的点加控制和倍点控制，使用乘法器和模约简以及其他必需的模运算单元来完成对应操作。由于表1～表4 的运算步骤仅仅是控制数据的选择输入和输出，所有运算都由模运算完成，中间计算结果也存储在寄存器堆，所以运算本身占用硬件资源较少。

3.3 模运算设计

模运算部分主要是模加减、模乘和模逆的设计。在点加倍点的操作周期中需要正常模加和模减单元各一个，还出现了特殊模运算单元，例如对于素数域中2 个数值M和N，需要计算3M、8M、1.5M−N、M−2N，以及模逆需要的0.5M，此类运算算法简单，均设置独立单元用于运算。此外，由于乘法消耗时间较长，为配合点加和倍点的周期操作，在模约简的输出端直接接入一个模加单元和一个模减单元，使模约简的结果可以直接进行模加减操作，从而能在一个周期内安排更多的操作，整个模运算部分的结构如图2 所示。

图2 模运算单元结构

模乘采用模约简结构，即先进行乘法运算，再对乘法结果做模约简。由于secp256r1 的数据位宽为256 位，Curve25519 曲线的数据位宽为255位，故直接采用单元库中已有的256 位乘法器，满足2 条曲线的位宽需求，并在一个周期内完成乘法。模约简需单独设计，secp256r1 曲线的p=2256−2224+2192+296−1，乘法操作后得到一个512位的乘法结果A，易知A＜p2，用二进制表示后分为16 个数据段，设A=A152224+A142192+…+A1232+A0，其中Ai的宽度为32 位，则约简公式如算法4所示[18]。

算法4secp256r1 的快速模约简公式

输入A=(A15||A14||A13||…||A2||A1||A0)

输出B=Amodp

快速约简通过多个数据的加减操作来实现，仅在最后一步取模运算。需要注意，由于S2的高位为0，因此最后得到的待约简数据至多有5 个进位或5 个借位，比较常见的方式是采用高位为0 的形式化简以上计算式，进行再次约简，但即使再次模约简，也会出现超过模p的情况，依然需要进行判断并计算输出。由于设计包含2 条曲线的模约简，需要考虑单元间的复用关系。

对于Curve25519，p=2255−19=2255−24−22+1，位宽为255 位，一次乘法操作的结果A在二进制下位宽最高位510 位，根据p的形式特点，设A=A2542508+A2532506+A2522504+…+A122+A0，Ai的宽度为2 位，利用此形式的A对p做模约简。

模约简过程分为两轮，第一轮处理高254 位，首先要对A的最高项A2542508做约简，需利用A2542253乘以p值，得到多项式A2542508−A2542257−A2542255+A2542253，消去最高项后得到剩余项A2542257+A2542255−A2542253，以此类推，直至用A12821乘以p得到多项式A1282256−A12825−A12823+A12821，消去A1282256项后得到剩余项A2542257+A2542255−A2542253。第一轮运算得到的约简结果分为两部分，第一部分是A的低256 位，即A1272254+…+A122+A0，此部分未操作，直接保留设为为T；第二部分是所有剩余项的和，整理后为A2542257+(A253+A254)2255+(A252+A253−A254)2253+(A251+A252−A253)2251+…+(A128+A129−A130)25+(A128–A129)23+(−A128)21，对第二部分的高两项进行第二轮约简，消去A2542257+(A253+A254)2255，得到新增剩余项为A25426+(A253+2A254)24+A25322−(A253+A254)。至此，两轮约简整理完毕，将各位置的数值按规律重新整理为和项和差项后，可得算法5 所示的快速约简算法。

算法5Curve25519 曲线快速约简算法

输入A=(A254||A253||A252||…||A2||A1||A0)

输出B=Amodp

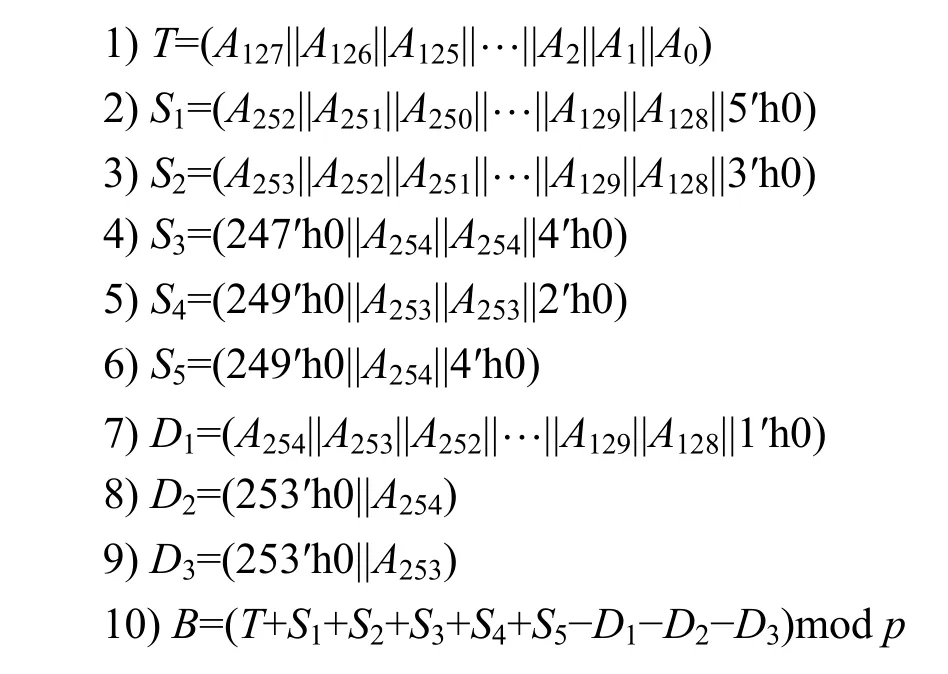
考虑到高位为0 的各部分，以及T所取的位数为256 位，最后一步待约简数据会有至多5 个进位或2 个借位，与secp256r1 曲线的情况基本类似，故采用加减法阵列计算出2 种模约简所有最后可能的输出结果，通过判断加减法的标志位来选择输出正确结果，其结构如图3 所示。

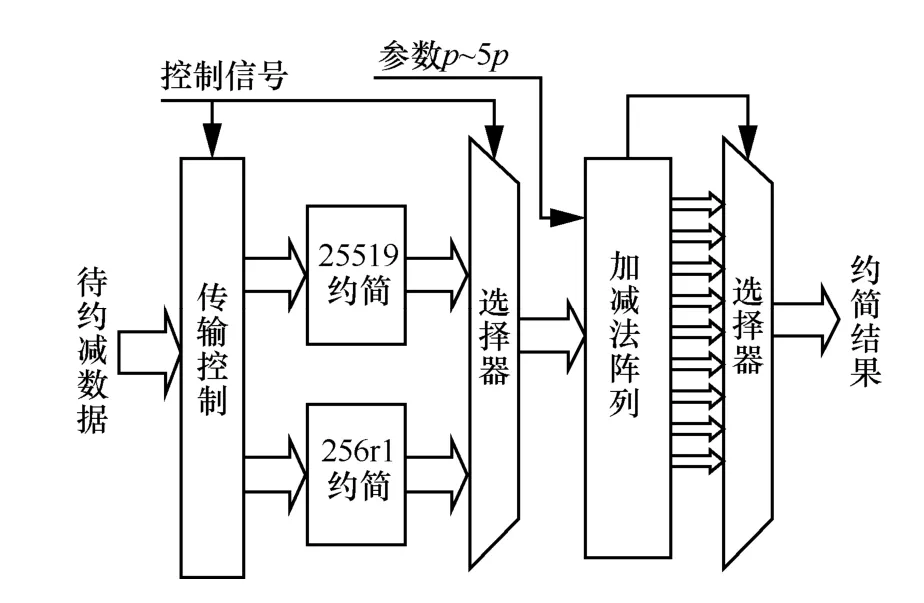
图3 模约简结构

加减法阵列中需参数p～5p参与运算，需要在寄存器堆中存放2 条曲线的5p参数，其中，参数p在标量乘中多次使用，设置为参数形式存储；2p在运算开始时通过p相加得到；3p通过3 倍模加单元计算得到；4p通过模减单元5p−p运算得到，这些值在首周期结束时固定在加减法阵列的输入端，并在次周期开始参与运算，与乘法前后衔接。

模逆运算使用二进制右移算法，其基本算法如算法6 所示[20]。

算法6二进制右移算法求模逆

输入素数p和a∈[1,p−1]

输出a−1modp算，算法中每次向右移位一次，并需要做除2 操作，但对于二进制计算很容易实现。如需更快的速度，则可以考虑每次右移2 位，但需要额外做除4 操作并需要更多的判断分支，故本文没有采用。考虑到使用标量乘进行椭圆曲线加密时也需要使用模逆运算，且与标量乘操作无时间上的冲突，所以将模逆模块单独引出，设立标志位以供标量乘内部使用或外部调用。

4 验证与实现

完整的标量乘工作流程如图4 所示。图4 仅表示了重要的操作步骤，点加Z和点加1 分别使用表2和表3 中的点加流程，临时寄存器在预计算和迭代计算部分都有使用，但图4 中未全部标出，模约简也未在图中给出。运算时各环节所需要消耗的时钟周期如表5 所示，其中包含了各工作状态之间转换消耗的周期数。

经综合后所得面积速度与文献[4-7,25-26]进行对比，得到表6 所示的结果，表6 中的AT是门数与单次运行时间的乘积。

表5 不同运算消耗周期情况

最终设计采用55 nmCMOS 工艺库综合，主频最高可到625 MHz，此主频下的门数为1 022×103个，按表5 中平均消耗周期计算，对于secp256r1曲线，计算基点的标量乘单次只需2.60 μs，每秒可计算38.5 万次；计算普通点的标量乘需要6.56 μs，每秒可计算15.3 万次；对于Curve25519，计算一次标量乘需要6.33 μs，每秒可计算15.8 万次。

图4 完整标量乘工作流程

表6 标量乘对比结果

本文设计消耗的门数是文献[4]的2.3 倍，最高主频提高了70 MHz，由于文献[4]采用分段多次迭代的方式实现模乘，而本文设计采用了256 位的乘法器配合模约简来实现模乘，频率受乘法器限制，故主频并未得到显著提升，但配合3.2 节中的点加倍点操作，可以实现乘法和模约简的二级流水，标量乘计算过程中每个周期都可以得到模乘结果，所以实际每秒标量乘的运算次数远超文献[4]。其余文献也类似，差异在于模乘分段位数是32 位、64 位还是128 位，如文献[5]采用的是128 位的分段模乘，每秒可计算标量乘8 万次，是所有文献中每秒运算次数最高的，但消耗的门数是本文设计的3.4 倍，同时本文设计的每秒运算量可达文献[5]的1.9 倍。文献[6-7,25-26]的门数消耗小于本文设计，但本文设计的主频和门数均约为文献[6]的3 倍，实际每秒运算次数远超文献[6]；文献[7]的门数为本文设计的52%，但主频只能到本文设计的30%，单次标量乘运行时间较短，但也是本文设计的18 倍；文献[25]采用较低门数完成设计，且能达到相对较高的主频，AT是所有文献中最小的，但也是本文设计的3.8 倍；文献[26]也仅在门数一项上低于本文设计，运算速度和AT与本文设计相比均无优势。以上数据比较发生在普通点的计算上，本文设计在签名时还能提供基点G的标量乘38.5 万次，适用于服务器端的高速运算。

5 结束语

本文面向椭圆加密的运算需求设计了标量乘单元，采用快速模约简的方式实现模乘运算，支持secp256r1 和Curve25519 曲线的标量乘，并能够在输入基点时得到更快的运算速度以应对椭圆曲线签名和公钥的生成需求，设计同时支持多标量乘以应对椭圆曲线验签使用，将模逆端口单独引出以应对签名和验签操作中的模逆需求，只需调用本单元即可完成加密算法中绝大部分操作。相较于其他设计，本文设计的运算速度有较大优势，能够提供secp256r1 曲线上每秒38.5 万次的基点标量乘和每秒15.3 万次的普通点标量乘，可以实现Curve25519 每秒15.8 万次标量乘。