基于注意力机制的泊位占有率预测模型研究

王竹荣，薛伟，牛亚邦，崔颖安，孙钦东，黑新宏

（西安理工大学计算机科学与工程学院，陕西 西安 710048）

1 引言

近年来，智能交通系统（ITS,intelligent transportation system）迅速发展[1]。停车诱导信息系统（PGIS,parking guidance information system）是ITS 中不可缺少的组成部分，泊位占有率预测是其中一项重要技术。根据国际停车协会（IPI,International Parking Institute）的一项调查，超过30%的汽车在公路上寻找停车位，而这些巡航汽车在城市地区造成了高达40%的交通堵塞[2]。研究数据显示，在公路的车流量中，泊车车辆占道路车流量的12%～15%。寻找车位的过程会增加30%的燃油消耗[3]。泊位占有率预测和泊位信息共享对停车场的日常运行、调度规划以及交通运行状态具有重要影响。泊位占有率预测已经引起学术界和工业界的广泛关注。例如，谷歌地图基于用户调查和轨迹数据[4]预测全市范围内的停车困难程度；百度地图基于环境上下文特征（如兴趣点、地图查询等），估计全市范围内的实时停车位可用信息[5]。上述方法是对某一区域的停车难度进行预测和分级，这可能导致对于单个停车场的泊位占有率预测结果不准确。

现有的泊位占有率预测方法主要为基于统计学的预测方法和基于机器学习的预测方法。基于统计学的预测方法虽然计算较为简单，时间复杂度较低，但是预测精度不高且稳定性较差。例如，Dunning 等[6]提出建立一个停车场数据收集以及泊位预测的PGIS，利用差分整合移动平均自回归模型进行泊位占有率预测，实验结果表明该模型的预测效果并不稳定，仅能预测占有率相对平稳的时间段，在出现波峰或者波谷的时间段预测效果较差。Caliskan 等[7]利用PGIS 采集的车辆抵达停车场的时间和停车场泊位占有率等历史数据，使用连续时间齐次马尔可夫与排队论预测方法进行泊位占有率预测。Chen 等[8]对泊位占有率预测展开研究，结合泊位占有率的外在影响因素，利用通用代数建模系统（GAMS,the general algebraic modeling system）进行建模求解，泊位占有率预测精度有一定提升。Rajabioun等[9]和Klappenecker等[10]通过数学方法进行泊位占有率预测，该方法依赖于参数控制，具有很强的样本依赖性，虽然降低了计算的时间复杂度，但稳健性较差。Richter 等[11]通过分析停车场的泊位历史数据，对泊位数据时间和空间进行聚类，来选择最优的时空特征，预测准确性进一步提高。为解决基于统计学泊位占有率预测方法的不足，基于机器学习的泊位占有率预测方法近几年大量涌现。杨兆升等[12]将BP（back propagation）神经网络应用到泊位占有率预测问题中。陈群等[13]利用相空间重构对泊位数据进行预处理，并利用Elman 神经网络泊位预测方法进一步提升模型预测精度。Blythe 等[14]和季彦婕等[15]提出基于小波变换的泊位预测模型，然后利用启发式算法对神经网络进行优化，提出粒子群优化的小波神经网络停车场泊位预测模型。陈海鹏等[16]采用小波变换和 ELM（wavelet transform with extreme learning）相结合的方法进行泊位的短时预测，所提模型在不降低预测精度的情况下，提升了传统神经网络的训练效率。韩印等[17]提出基于灰色−小波神经网络的有效泊位预测算法。

综上分析可知，基于统计学的泊位预测方法在时间复杂度方面具有优势，但是预测精度相对较低且样本依赖性强。与之相比，基于机器学习的泊位预测方法的预测精度大幅提升，适合时间跨度较长的泊位预测场景要求。

泊位占有率预测是一种具有典型时间序列特征的时间序列预测问题。随着深度学习在图像处理和自然语言领域的发展，很多新的神经网络模型和方法被用于时间序列预测问题，如Seq2seq 模型结合残差网络[18]、深度神经网络结合统计学方法的ARMAM（autoregressive moving average model）[19]、基于注意力机制的长短时记忆网络[20]、基于时间注意力学习的多视野时间序列预测方法[21]、基于时间模式的神经网络[22-23]、基于DTW（dynamic time warping）的直觉模糊时间序列预测模型[24]和利用直觉模糊多维取式推理建立的高阶模型[25]。其他的模型介绍如下。自注意力机制转移网络模型[26]通过矩阵控制序列权重的学习方式学习特征信息，主要适用于自然语言处理问题，是目前自然语言处理研究和应用最为广泛的模型。自注意力机制的卷积模型[27]通过改变自注意力机制结构，将原有的注意力用于计算全局的隐含层向量权重，此模型利用卷积神经网络（CNN,convolutional neural network）获取局部信息，将时间复杂度从O(n2)降低到O(n(logn)2)，加快了运算速度。基于社会注意力的行人轨迹预测模型提高了预测的可解释性和预测精度[28]。何坚等[29]提出了综合考虑多维时空因果关系的泊位占有率预测技术和方法。梅振宇等[30]对泊位占有率序列的复杂性度量方法进行了分析。

从长远发展角度考虑，PGIS 不仅要及时地为用户提供的泊位信息，还应对未来一段时间的泊位需求信息做出预估，给予用户更长时间进行出行规划。因此，泊位的中长期预测研究是必要的。目前，对泊位占有率中长期预测的研究相对较少，现有的预测方法主要以传统的迭代计算为主，预测效果较差。深度学习方法提供了处理多元时间序列的预测新思路。对泊位的中长期预测方法进行研究，在增加预测步长的前提下，提升预测精度及预测序列的稳定性指标成为必要工作。

本文主要工作如下。1)提出了一种高效的时间序列预测模型。所提模型以sequence-to-sequence 为整体框架，以双向长短时记忆（BiLSTM,bi-directional long short-term memory）网络[31]为模型的编码器和解码器的内部结构，通过一维CNN 提取多变量的局部特征作为模型的注意力机制，捕获泊位预测问题特征的时间模式信息。2)将所提模型用于预测泊位占有率数据预测，测试结果及对比分析表明，所提带有注意力机制的神经网络模型有较强的非线性特征提取能力，与 LSTM（long short-term memory）网络模型相比预测精度较高，有较强的稳健性和稳定性。

2 基于注意力机制的sequence-to-sequence泊位预测模型

sequence-to-sequence 模型实现了从一个序列到另一个序列的转换。Google 曾用 sequence-tosequence 模型加注意力机制来实现翻译功能。sequence-to-sequence 模型突破了传统的循环神经网络（RNN,recurrent neural network）模型输入输出序列大小固定的限制。sequence-to-sequence 由编码器（encoder）和解码器（decoder）两部分组成，能有效提取输入数据的特征。停车场泊位数据具有典型的时间序列特征，通过历史数据预测未来停车场占有率，符合序列到序列模型的时间数据序列特征。因此，本文利用sequence-to-sequence模型结合时间模式的注意力机制进行泊位占有率预测。

本文采用sequence-to-sequence 编解码器结构作为泊位预测模型，其中编码器和解码器采用BiLSTM 网络。编码器端将不定长序列输出为定长序列，由于输入序列较长，解码器端难以获得有效的数据信息。因此，本文引入注意力机制，增强局部数据特征学习能力，保留BiLSTM 编码器对输入序列的输出，通过CNN 获得多变量的时间模式信息，并存储上下文信息。通过对模型进行训练，根据学习特征信息，将输入序列与模型输出关联起来，并对相关性高的序列分配较高的学习权重，用输出序列提取高度相关的有用特征。解码器将结合编码器输出信息及注意力机制存储的时间模式信息，输出预测目标序列。

2.1 BiLSTM 工作原理

BiLSTM 是双向LSTM，由前向LSTM 与后向LSTM 组合而成，它们用来建模上下文信息，具有更强的长期信息记忆能力。

BiLSTM 的单元结构如图 1 所示，其中(x1,x2,…,xm)为输入序列，LSTML为前向LSTM，LSTMR为后向LSTM，hLm为前向LSTM 隐藏状态向量，hRm为后向LSTM 隐藏状态向量，ht为BiLSTM 的隐藏状态向量。BiLSTM 的隐藏状态需要结合前向和后向2 个方向的隐藏状态。

BiLSTM 的隐藏状态向量为

BiLSTM 是由2 条LSTM 链式结构组成，而LSTM 的内部结构可参见文献[32-33]。

BiLSTM 中的单向LSTM 描述如下。每一个步长t与其对应的输入序列为X={x1,x2,…,xw}（w为滑动窗口大小），网络内部单元中包括输入门it、遗忘门ft、输出门ot和隐含层ht。状态单元ct通过控制it、ft和ot来控制数据的记忆及遗忘，如式(2)～式(9)所示。

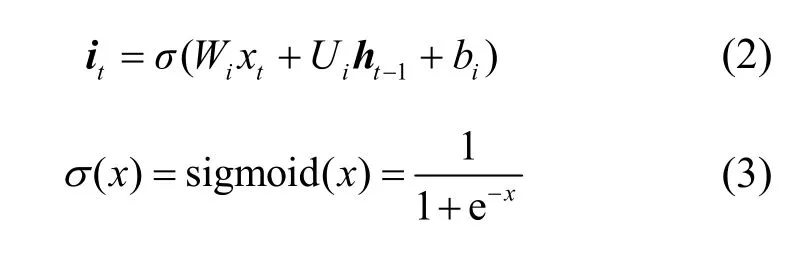
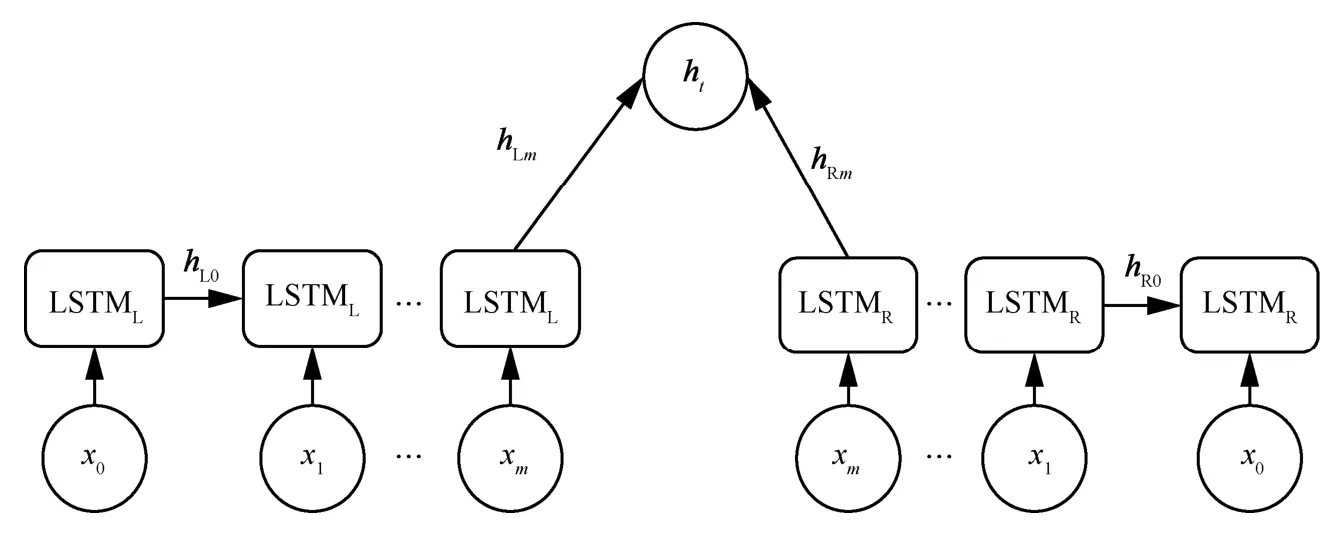
图1 BiLSTM 单元结构

其中，Wi、Wf、Wo、表示输入过程的权重参数，Ui、Uf、Uo、Uc表示状态转移权重参数，b i、bf、bo、bc表示偏差参数，表示候选记忆细胞，tanh(⋅)表示双曲正切函数，·表示点乘。

sigmoid 函数σ(x)为一个logistic 函数，它可以将一个实数映射到(0,1)。tanh(⋅)是双曲正切函数，它可以将数值缩放到(−1,1)。三类门限控制单元共同控制信息进入和离开记忆细胞，输入门it调节进入记忆细胞的新信息，遗忘门ft控制记忆细胞中保存的信息，输出门ot定义输出信息。LSTM 的门结构使时间序列上的信息形成一个有效的依赖关系。

2.2 sequence-to-sequence 模型结构

sequence-to-sequence 模型在处理序列任务时，对输入序列或输出序列的长度没有限制，可执行不定长输入和不定长输出。sequence-to-sequence 模型结构如图2 所示。

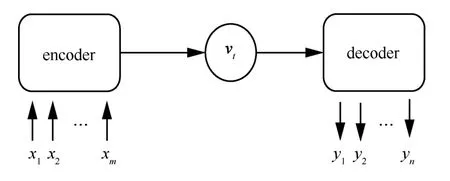
图2 sequence-to-sequence 模型结构

图2 中，sequence-to-sequence 模型由编码器、上下文向量vt和解码器组成。编解码器通常是多层的RNN 或LSTM 结构，本文选择BiLSTM 网络作为编码器和解码器网络。上下文向量vt包含了x1,x2,…,xm隐含层编码信息。对于时间t，将编码器隐含层ht、解码器之前时刻的输出yt−1、之前时刻的隐含层状态st−1以及vt输入解码器。最后得到解码器的隐含层状态st，解码器对输出值进行预测。

sequence-to-sequence 编解码器结构模型计算式如式(10)和式(11)所示。

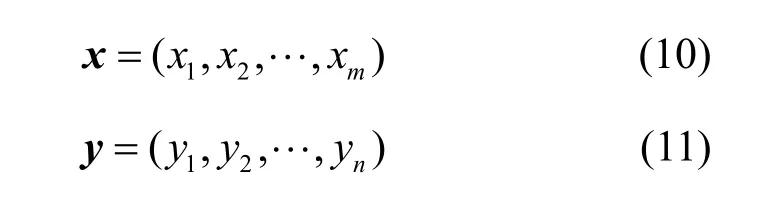
其中，x和y分别为sequence-to-sequence 编码器端输入序列和解码器端最终输出预测值。

编码器输入端是x和上一个时间步的隐藏状态ht−1，输出端是当前时间步的隐藏状态ht，即

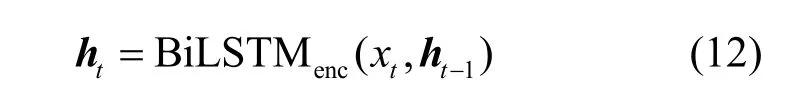
对原始时间序列使用BiLSTMBlockCell 处理，得到每个时间步的隐藏状态hi（hi为列向量），每个hi维度为m，w是滑动窗口长度，得到的隐藏状态矩阵。隐藏状态矩阵的行列向量意义如下。

1) 行向量代表单个变量在所有时间步的状态，即同一变量的所有时间步构成的向量。

2) 列向量代表单个时间步状态，即同一时间步下的所有变量构成的向量。

2.3 TPA 机制

所提模型中利用一维CNN 学习时间序列数据的时间模式信息，即TPA（temporal pattern attention）作为网络的局部特征学习方式[23]。TPA 机制结构如图3 所示。图3 中最左侧箭头表示对变量的处理，每一行表示一个变量的时间序列数据。通过卷积计算获得该变量在卷积核范围内的时间模式矩阵，评分函数计算时间模式矩阵的分值，并通过sigmoid 函数将分值归一化，获得注意力权重α，结合时间模式矩阵及注意力权重计算得到上下文向量vt。将encoder 中的上下文向量vt及隐藏状态ht，与decoder 中的隐藏状态st进行连接，并通过输出层及softmax 函数来计算输出预测值。

以下详细描述TPA 机制在所提模型中的作用机理。

首先，利用一维CNN 进行卷积计算。

卷积配置为k个滤波器（filter），卷积核（kernel）尺寸为1×T（T代表注意力所覆盖的范围，通常令T=w），将上述kernel 沿隐藏状态矩阵H的行向量计算卷积，提取该变量在该卷积核范围attn_length内的时间模式矩阵如式(13)所示。

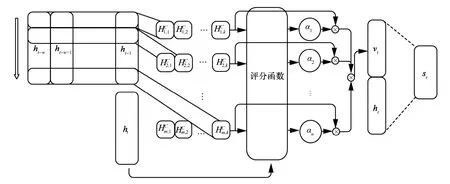
图3 TPA 机制结构

对上述学习到的时间模式进行评分，时间模式的评分函数f为

注意力权重αi为

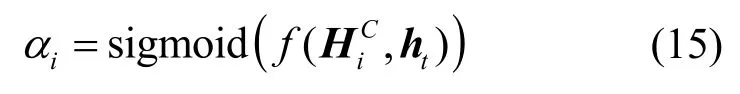
对HC的每一行做加权求和，得到上下文向量vt为

其中，αi为时间模式矩阵HC的第i行注意力权重，为时间模式矩阵HC的第i行。

将上下文向量vt与encoder 的隐藏状态ht传入decoder。将encoder 的隐藏状态ht、上下文向量vt与decoder 隐藏状态st连接，如式(17)所示。

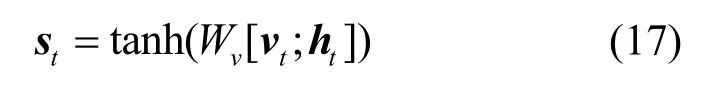
其中，Wv为权值参数。

decoder 通过接收前一个输出序列yt−1以及decoder 的上一个时间步的隐藏状态st−1和上下文向量vt计算当前隐藏状态st，如式(18)所示。

最后，结合decoder 当前时间步隐藏状态st及上下文向量vt，通过输出层及softmax 函数来计算输出yt，如式(19)所示。

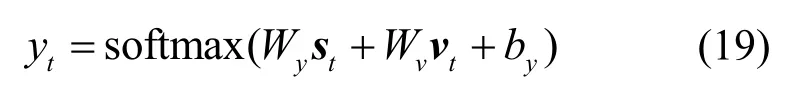
softmax 函数是一个概率函数，max 表示取大概率最大值，它的作用是将所有输出映射到(0,1)，softmax 最大值作为最终的输出。

假设有一个数组Y，数组长度为k，yi表示Y中的第i个元素，那么元素yi的softmax 值为

2.4 基于注意力机制的sequence-to-sequence 泊位占有率预测算法

泊位占有率预测过程如图4 所示。首先，获取目标停车场历史停车数据信息；然后，对数据进行清洗及预处理，对基于注意力机制的sequence-to-sequence泊位预测模型进行训练；最后，将训练好的预测模型进行泊位预测。基于注意力机制的sequence-to-sequence 泊位占有率预测算法流程如图5 所示。

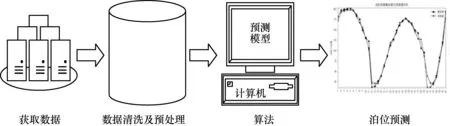
图4 泊位占有率预测过程

图5 基于注意力机制的sequence-to-sequence 泊位占有率预测算法流程

基于注意力机制的sequence-to-sequence 泊位占有率预测算法如算法1 所示。

算法1基于注意力机制的sequence-to-sequence泊位占有率预测算法

1) 输入原始数据；

2) 对数据进行清洗及预处理，包括缺失数据填充、剔除无用数据、数据标准化和归一化；

3) 进行特征相关性计算和检验；

4) 划分训练集和测试集；

5) 建立基于sequence-to-sequence 泊位预测模型结构；

6) 构建TPA 机制层；

7) 用训练集训练基于注意力机制的sequence-to-sequence 泊位预测模型及结构参数，得到训练好的预测模型；

8) 通过将测试集输入训练好的预测模型得到预测结果。

2.5 时间序列预测的评价指标

本文采用均方根误差（RMSE,root mean squared error）和平均绝对误差（MAE,mean absolute error）对所建模型的预测结果进行度量。RMSE 和MAE 计算式如式(21)和式(22)所示。

其中，n表示样本数，di表示一组测量值与真实值的偏差，xi表示真实值，表示预测值。

MAE 范围为[0,+∞)，当预测值与真实值完全吻合时MAE=0，为完美模型，误差越大，MAE 越大。RMSE 描述所有预测结果的偏离程度，而MAE 在对预测结果进行评价时，可克服误差相互抵消的问题，因此对于实际预测误差大小的反映更为准确。

3 实验分析

3.1 测试数据集

本文测试数据来自加州大学欧文分校（UCI,University of California Irvine）的停车场数据库UCI，该数据集包括伯明翰市某区域内29 个停车场从2016 年10 月4 号至2016 年12 月19 号之间的36 285 条数据。数据信息包含停车场ID、停车时间、停车场的泊位数、已有车辆。本文使用数据集中包括BHMBCCMKT01 在内的28 个停车场的停车数据作为实验测试数据。

所提模型选取泊位入驻数、天气、节假日、工作日作为模型的4 个特征。首先对数据集中数据缺失值进行临近均值填充，然后对数据集进行归一化处理。对每个单个停车场数据集进行划分，其中80%为训练集，20%为测试集。

本文测试分为两部分，第一部分测试所提模型的结构，并通过消融实验，重点测试所提模型带有注意力机制和不带注意力机制的数据及对比分析；第二部分测试所提模型对停车场数据的测试结果及对比分析。

3.2 所提模型结构确定

本文采用sequence-to-sequence 编解码器结构来预测泊位占有率，采用BiLSTM 结构进行编解码操作，然后通过BiLSTM 层数优化模型参数。最初实验的学习率设置为0.01，衰减率设置为0.5，隐含层节点的数量设置为64，CNN 设置4 个滤波器，卷积核大小为1 × 18。将数据集输入网络进行训练，测试编码器和解码器不同层数BiLSTM 网络的RMSE 变化情况。

本文分别对单层、双层、三层、四层及五层BiLSTM 进行测试，并记录各自的RMSE 变化过程。测试结果表明，当模型经过多次迭代RMSE 趋于稳定时，采用单层、四层BiLSTM 结构的训练RMSE较大，经过双层、三层及五层BiLSTM 结构训练RMSE 相对较小且三层为最小。因此，本文选择编码器解码器内部BiLSTM层数为RMSE最小的三层BiLSTM。在深度学习中，模型通过训练从数据样本中学习所有样本的变化规律，容易导致过拟合或欠拟合。通过增加模型训练迭代的次数，可以克服模型拟合不足的现象。对于过拟合的处理，对神经单元以一定概率断开dropout，dropout 通过概率断开神经网络之间的连接，减少每次训练时实际参与计算的模型的参数量，从而减少了模型的实际容量，来防止过拟合。需要注意的是，在测试时，dropout 会恢复所有的连接，保证模型测试时具有更强的泛化特性，使预测结果具有更好的多样性。本文中dropout 概率设置为0.5。

3.3 泊位占有率模型确定与数据预测

以下实验将利用所提模型分别对单个停车场BHMBCCMKT01和总体28个停车场的泊位占有率进行仿真测试。

3.3.1单个停车场数据测试分析及对比实验

本节首先进行所提预测模型有注意力机制和无注意力机制在不同步长下对单个停车场数据执行预测的误差对比分析，然后给出不同预测模型对单个停车场数据的预测精度的对比。

当训练sequence-to-sequence 模型时，使用迭代预测，并且通过选择模型的参数来获得实验结果。sequence-to-sequence 泊位预测模型参数如表1 所示，输出步长为36，编码器端BiLSTM 隐含神经元的个数E_hidden 和解码器端BiLSTM 隐含神经元个数D_hidden 均为64，学习率Learning_rate 为0.001，遗忘率 Drop_rate 为 0.75，输入特征数Input_dim 为4，迭代次数Epoch 为1 000，输入数据长度Time_step 为18。

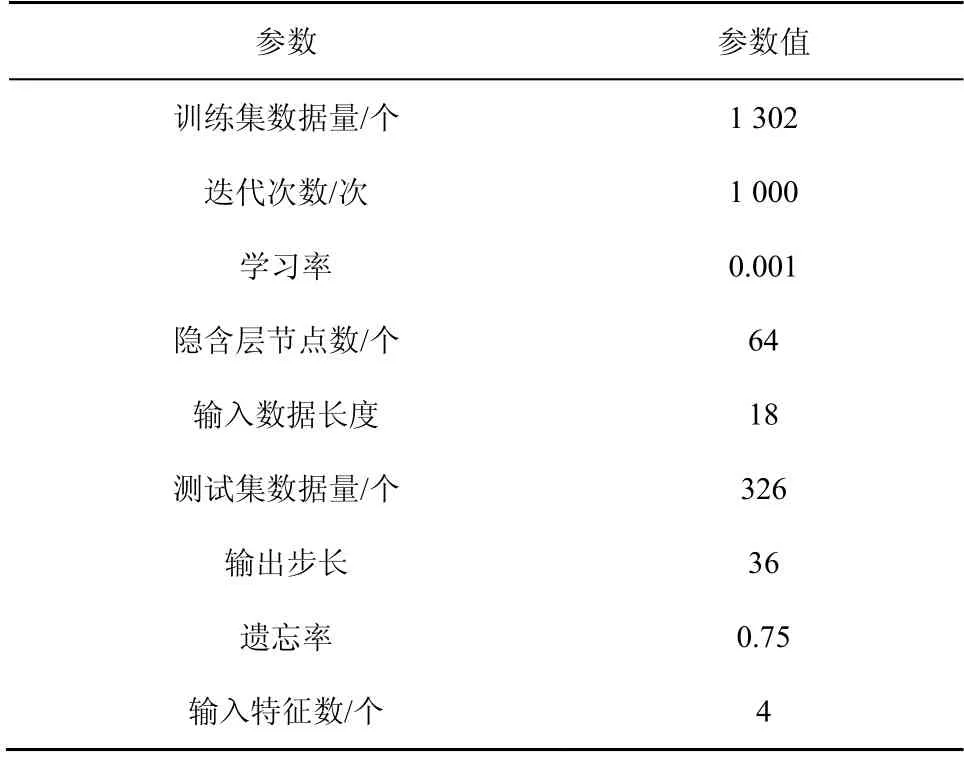
表1 sequence-to-sequence 泊位预测模型参数

表2 为所提模型有注意力机制和无注意力机制对数据集BHMBCCMKT01 的预测值与真实值对比，图6 和图7 为相应预测值与真实值对比曲线。图8 为所提模型有注意力机制和无注意力机制下泊位预测MAE 随步长变化的曲线。

由表2 数据可知，有注意力机制的预测数据平均误差为6.75，无注意力机制的预测数据平均误差为17.75。对比图6 和图7 可以看出，注意力机制在所提模型中具有重要作用。从图8 可以看出，所提模型无注意力机制时，其MAE 随步长的增加上升较快；而有注意力机制时，其MAE 随步长的增加上升较慢。

当利用所提预测模型预测未来36 个目标步长的停车场泊位占有率时，其对应的真实值为194，而预测值为178，其误差为16，预测结果可以满足实际预测精度要求。综上分析可知，所提模型在步长取较大值时预测结果的误差相对稳定，模型可达到较好的预测效果。

3.3.2多个停车场数据测试分析

使用28 个停车场作为实验数据，并对每一个停车场数据集按4:1 进行数据划分，然后进行模型训练和测试。使用基于注意力机制的sequence-tosequence 预测模型同LSTM 预测模型进行对比分析。表3为泊位占有率预测最小MAE，显示了sequenceto-sequence 泊位占有率预测模型以及LSTM 泊位预测模型在数据集上的总体效果。LSTM 预测模型的预测步长为10，sequence-to-sequence 预测步长为36，从表3 中可以看出，sequence-to-sequence 泊位预测模型在28 个停车场的数据集测试中，有23 个预测结果的MAE小于或等于LSTM泊位预测模型。sequence-to-sequence 泊位预测模型MAE 的中位数（median）为0.021，LSTM 泊位预测模型MAE 的中位数为0.025。sequence-to-sequence 泊位预测模型MAE 的平均值（mean）为0.024，LSTM 泊位预测模型MAE 的平均值（mean）为0.028。sequenceto-sequence 泊位预测模型MAE 的最大值（max）为0.059，LSTM 预测模型MAE 的最大值（max）为0.078。sequence-to-sequence 预测模型MAE 最小值（min）为0.010，LSTM 泊位预测模型最小值（min）为0.008 6。从整体来看，sequence-to-sequence 泊位预测模型预测结果MAE 的中位数、平均值、最大值均优于LSTM 泊位预测模型。

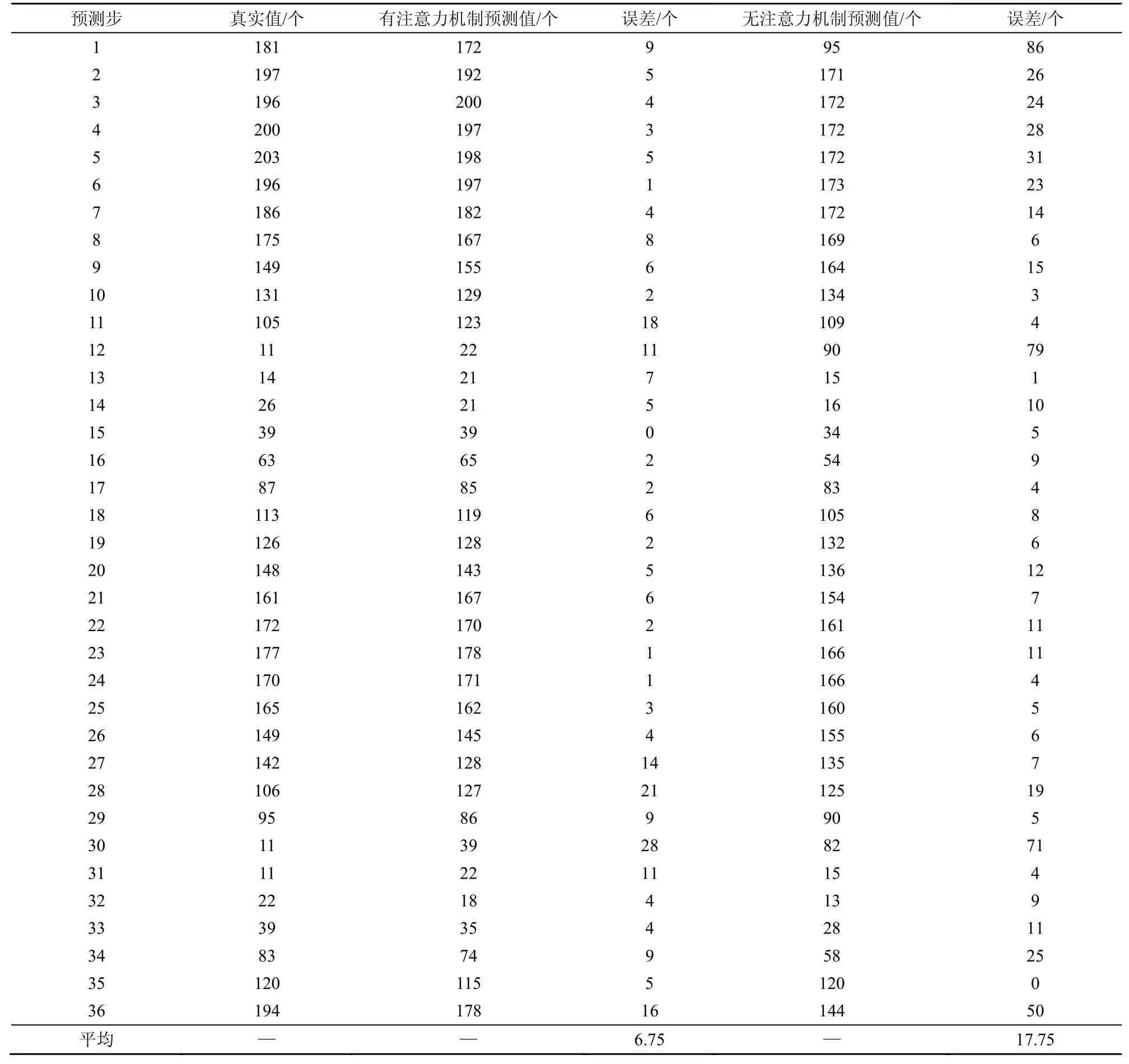
表2 所提模型有注意力机制与无注意力机制的预测值与真实值对比（步长=36）

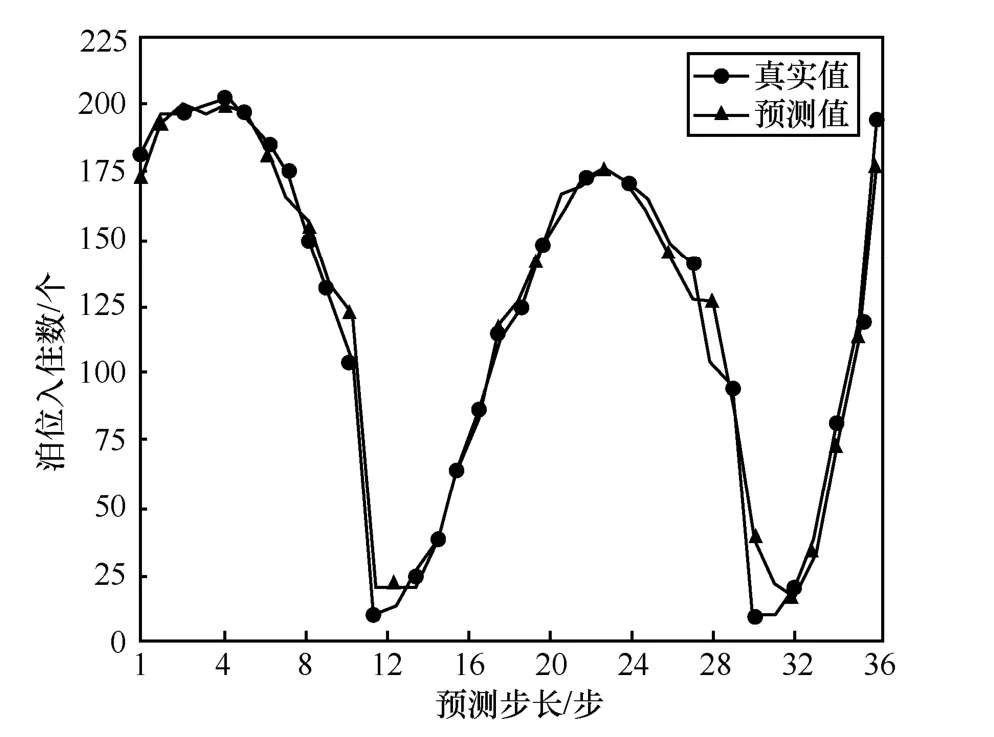
图6 sequence-to-sequence 有注意力机制模型预测值与真实值对比曲线

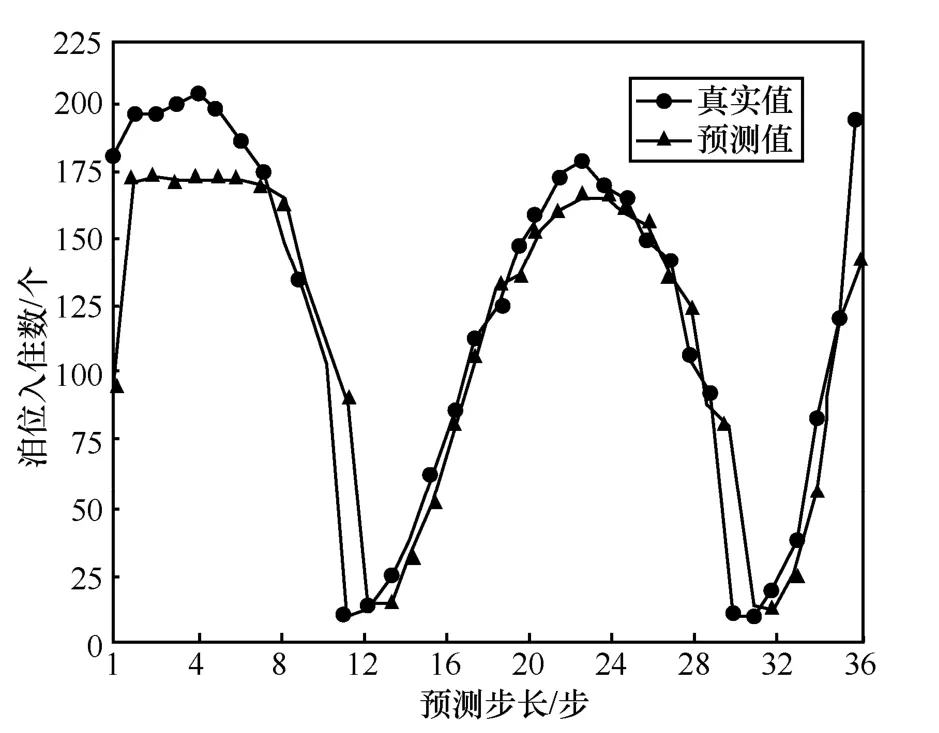
图7 sequence-to-sequence 无注意力机制模型预测值与真实值对比曲线

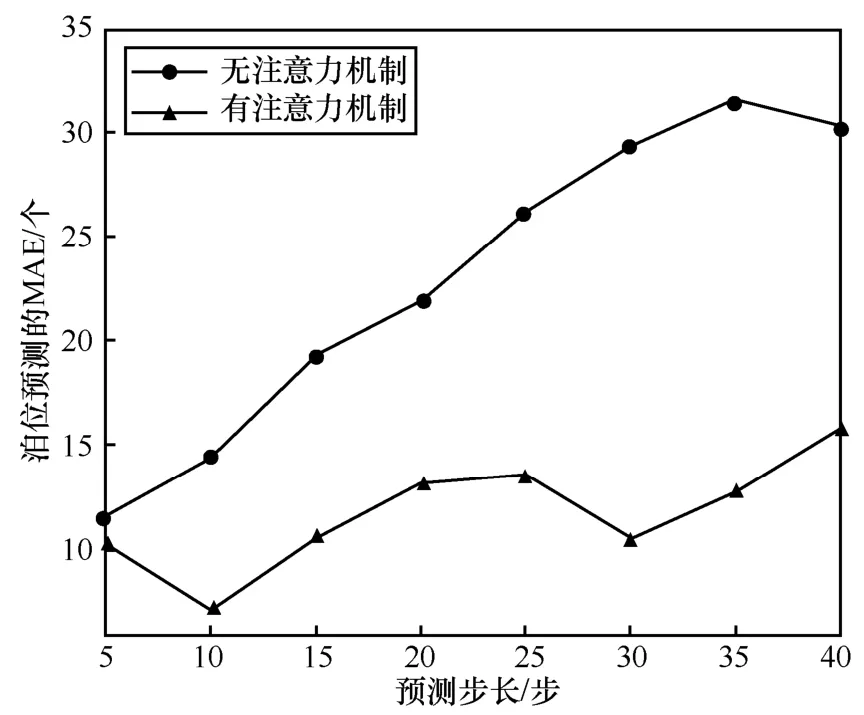
图8 所提模型有注意力机制和无注意力机制MAE 随步长变化的曲线

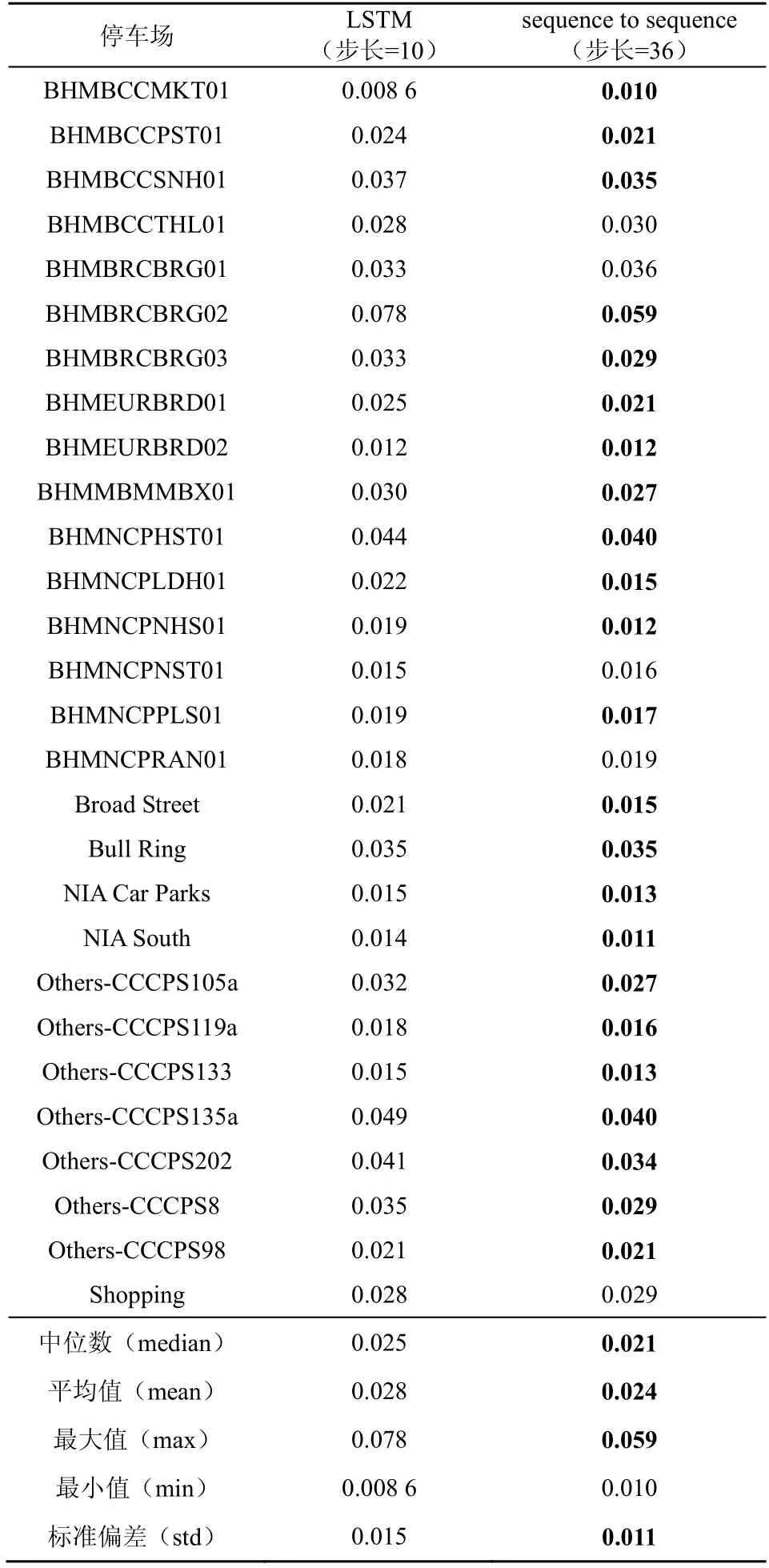
表3 泊位占有率预测的最小MAE 对比数据

如图9 所示，sequence-to-sequence 泊位预测模型预测结果的MAE 更为集中且相对更小。因此，sequence-to-sequence 泊位预测模型预测精度整体优于LSTM 泊位预测模型且更为稳定。

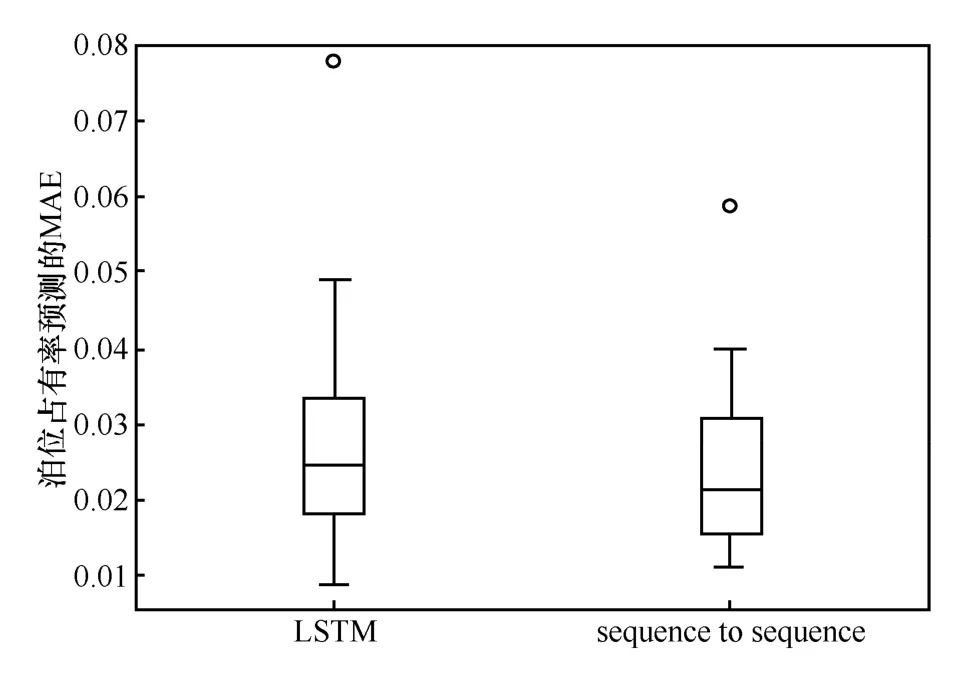
图9 sequence to sequence 模型与LSTM 模型MAE 箱线图分布

综上所述，基于注意力机制的sequence-tosequence 泊位预测模型在泊位预测中，在增加了预测步长的前提下预测精度和稳定性均有提升。

4 结束语

本文以泊位占有率的预测作为研究对象，提出了一种基于注意力机制的sequence-to-sequence 模型对泊位占有率问题进行求解，为了提高泊位占有率的预测精度，在模型中将天气、工作日、节假日等特征作为泊位占有率的融合特征，使模型的泛化能力更强，精度更高。在本文的预测模型中，利用时间模式注意力机制捕获数据的局部特征，利用sequence-to-sequence 模型多输入多输出的特性，使模型的拟合能力更强。通过对模型的训练和参数调整，对测试集进行测试，使用RMSE 和MAE 对模型预测结果进行评估，结果表明，所提模型表现出更好的预测效果。将所提模型与LSTM 模型的泊位占有率预测算法得到的预测数据进行比较，验证了所提模型和方法的有效性。在未来工作中，将对存在奇异点和噪声数据集的处理进行研究，并考虑泊位占有率的空间特征关联信息，设计处理更为复杂情形的预测模型，致力于模型的理论分析和可解释性，进一步提高预测精度，并推广预测模型的应用前景。