一道经典几何题的解法探究与教学思考

殷高瞻 杨秀丽

摘 要：如果学生在问题的解决过程中，能抓住问题的本质，充分审视每个条件，多角度看问题，懂得推理的方法，那么他的逻辑思维水平会大大的提高。归纳和演绎是逻辑推理的两个方面，归纳推理的命题范围由小到大，结果是或然的，其作用是发现结论;演绎推理的命题范围由大到小，结果是必然的，其作用是证明结论。逻辑推理是科学发现的基本途径，两个方面不可偏废。下面笔者通过一道几何问题的多解情况展示逻辑推理在问题探究和解决中的作用。

关键词：逻辑推理;蝴蝶形;中点证明;一题多解;多解归一

一  试题呈现

立意分析：本题属于中点证明类综合题。在坐标系的背景下，考察全等三角形的性质与判定，结构简洁，内涵丰富，充分体现了中点证明的多角度性。通过让学生经历观察、猜想、思考、推理、归纳等过程来探究图形的本质特征。以此考察学生独立思考、推理、综合分析问题和解决问题的能力。该题具有入口宽、出口窄、综合性强、区分度好等特点，具备了经典题的基本特征，能有效和可信的评价学生數学核心素养，具有良好的解题导向功能。

二  解法探究

解法1：作垂线构造蝴蝶形证中点法

如图2，猜想. 连接AF，CE，则可得≌，所以，，再根据作垂线构造蝴蝶形证中点法，过点A作交EF的延长线于点H，过C作交EF于点T，只要证出AH=CF，只要证≌，即可得到AG=CG. 因为OF=OE=2，所以，设，则，所以≌，所以AH=CT，所以≌，所以AG=CG.

解题反思：方法1中本着作垂线构造蝴蝶形证中点的方法，通过发现并证明≌，得到AF=CE，通过导角得到，从而得到，发现并证明了≌，从而得到AH=CT，最后证明≌，从而使得问题得到解决，三次全等，顺理成章，虽然复杂，却也可解。

解法2：作平行构造蝴蝶形证中点方法

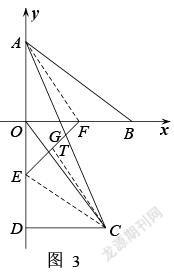
如图3，连接CE，AF，在方法1中已经说明了，，看，和猜想到AG=CG，即是要证G为AC的中点，根据作平行构造蝴蝶形证中点法，添加辅助线，过点C作交EF于点T，欲证，这两个三角形三个内角都分别相等了，缺边，需证CT=AF或FG=TG，结合CE=AF，可证CE=CT，导角可得，又因为，，所以，根据等角对等边得CE=CT，CT=AF，从而解决了问题。

解题反思：这个方法比之方法1，在过程书写上，要简洁一些，可是在思维量上，却又多出一些。关键是导角得到，而后得到第二次全等的关键要素CT=AF. 既然过点C作AF的平行线可以，那么过点A作CE的平行线也是可以的，过程同解法2，本文不再赘述。

解法3：通过审视题目的条件，观察、分析发现，OE=OF=2，，猜想AG=CG，欲证线段相等，八年级上人教版教材中，常用方法是证全等。AG在中，想到尝试过点C作轴交EF的延长线于点T，交x轴于点R，可得为等腰直角三角形，通过计算长度可得，，，，所以AE=CT，所以，从而证出AG=CG，使问题得到很好的解决。

解题反思：在几何问题的思考中，往往忽略代数计算的因素，从而错失完美的解题方法而走一些弯路。这种方法，充分考虑到了坐标系中的关键点的坐标，运用代几结合的思想，稍加分析，结合构造蝴蝶形证中点法，添加辅助线，稍加计算得出了蝴蝶形全等的关键要素——AE=CT，令人发自内心的叫好！

三  解题导向

1. 加强数学建模思想的渗透

教什么，如何教？这是教师教学的永恒课题。基于数学核心素养的数学教学，不仅需要模仿、记忆，更需要理解，感悟。《义务教育数学课程标准》（2011年版）在“前言”中指出：“义务教育阶段数学课程在呈现作为知识与技能的数学结果的同时，应重视学生已有的经验，使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程。”经典例题蕴含着丰富的教学资源，教师要很好的挖掘。利用一些经典的问题，经典的解法，加强数学建模思想的渗透，将知识、题型、解法归类和模型化，比如本题中中点模型之作垂线构造蝴蝶形、作平行线构造蝴蝶形、代几结合计算线段长度直接借助坐标轴构造平行等等，使学生能够辨认它属于哪一类基本解题模型，使解题有章可循，有法可依，从而提高解题效率，并通过不断积累运用，内化为自己的知识经验。比如本题中看到，就想到等腰直角三角形，可以帮助自己导角，导边，扫清全等关键要素的障碍。

2. 注意一题多解和多解归一

一题多解，对于开阔学生思路，发散学生思维，提升学生逻辑思维能力，消化理解知识，融会贯通，有着许多优点，但这往往是教师的一厢情愿。因为人的思维本身是有惰性的，当一个学生解数学题时，特别是综合题，能够找到一种解法已经很不容易，因此往往在寻找到一种解法时，是没有意识去寻找新的解法的。另外，思维是有惯性的，在没有外力的情况下，学生很难跳出已有的思维模式，往往会一条道路走到黑，如何能解决这些问题呢？这就要发挥解题教学功能了。解题教学的过程就是一种观察、尝试、猜想、探索、实验、论证、发现的过程，教师一定要带领学生读懂条件和结论，抓住题目中的条件特征、结论特征和图形特征，从中寻找突破口。当呈现一种解法后，教师要及时追问：还有其它解法吗？学生由此展开不同思路的探究与交流，并尽可能多地展示学生不同的思路和方法，最终比较解法优劣，优选最佳方法。同时，教师还要引导学生提炼各种解法的共性，进行多解归一。比如本题，通过宏观思考，我们会发现，前两种解法第一次全等是相同的，导角的方法也是运用补角的定义，三种解法都运用了构造蝴蝶形证中点法，这可以加深学生对数学的理解，促进对通性通法的认识，提高解题技巧与能力，增强逻辑思维能力。没有比较就没有鉴别，一题多解和多解归一的教学策略可以改变学生思维的方式，让学生有一种如梦方醒的感觉，如本题对第三种方法发自内心的叫好，能够使学生跳出已有的思维模式，有意识、有目标地多角度、多起点、多层次，立体地、全方位地思考问题。因此，对学生数学核心素养的培养而言，一题多解和多解归一的教学是要比多解几道题更为有效。

参考文献：

[1]李爱民.在问题解决中提升逻辑推理素养[J].中学数学（初中版）.2019（2）：21.

[2]白雪峰.一道中考压轴题的解法探究与教学思考[J].中学数学（初中版）.2018（2）：28-29.