基于相关个体拷贝数变异数据的趋势检验及在孤独症数据中的应用

吕梦轩，王昱泉，胡跃清

(复旦大学 生命科学学院 生物统计学与计算生物学系，上海 200433)

基因组的结构变异包含单核苷酸变异(Single Nucleotide Variants，SNVs)、小段的插入或缺失(Indels)、拷贝数变异(Copy Number Variations，CNVs)以及大片段的结构变异(Structural Variants，SVs)[1].拷贝数变异属于中等规模的结构变异，通常指长度在1kb以上5Mb以下的基因组片段拷贝数的异常增加或减少[1].其产生机制主要有非等位同源重组、非同源末端连接和DNA复制错误[2].总变异的12%可以归为拷贝数变异[3].综观文献，已报道的拷贝数变异位点超过55万个[4]，其中约一半所处的位置与蛋白编码区域重叠[5]，而发生在这些区域内的拷贝数变异可能会导致基因融合、基因断裂、隐性基因显性化[6]等现象，从而影响到相关基因的表达甚至直接改变基因的功能[6].和单核苷酸多态性(SNPs)类似，虽说拷贝数变异并不都是有害的，但已有众多的研究报道指出拷贝数变异与人类多种疾病有关，例如高血压[7]、孤独症谱系障碍[8]等.因而拷贝数变异是当今基因组学的一个重要研究对象.早期用于检测拷贝数变异的技术有人类染色体核型分析、荧光原位杂交等，其缺点是精度较低，且无法进行全基因组水平的检测[9].基因芯片技术[10]与二代测序技术[11]的发展提升了拷贝数变异检测的精度.二代测序技术在精度和通量上都有优势，而基因芯片的成本较低.

目前与拷贝数变异数据相关的研究大多专注于如何对拷贝数变异进行检测与定位，而针对它与疾病关联分析的方法不多，并且有的方法也存在着一定局限性.例如直接分析原始数据的研究方法容易受到背景误差的干扰，不同批次之间的数据可能会带来偏差[12].此外，多数方法只适用于一种结构类型的研究对象(基于人群的病例-对照数据[13]或是传统的家系数据[14])，并不能直接应用于既包含相关个体，又包含不相关个体的数据集(例如相关病例-不相关对照(Related cases-unrelated controls)数据集).针对家系数据的研究方法通常仅关注父母与患病孩子的3人组结构，针对群体数据的研究方法通常仅适用于普通的病例对照数据.基于现有方法存在的一些不足以及拷贝数变异数据的特点，本文改进了Cochran-Armitage趋势检验(Cochran-Armitage Trend Test，CATT)[15-16]，提出了适用于相关个体拷贝数变异数据的趋势检验(Modified Trend Test，MTT)方法，使其能够适用于研究对象中包含相关个体的情形.随机模拟结果表明MTT在多种情景下都具有较好的功效表现.同时借助于MTT有较广的适用范围，比较了几种不同数据采集方案的相对功效，结果表明相关病例-不相关对照具有较高的性价比.将MTT应用于孤独症真实数据的分析，检测出与疾病显著相关的拷贝数变异位点和位点上的相关基因，并通过基因功能富集分析与文献检索说明了结果的可靠性，这为后续研究提供了指引.

1 符号与方法

考虑到数据有可能来源于不同的技术平台，我们把拷贝数分为两类：可基因分型(Genotypable)，指每条染色体上的拷贝数都已知；不可基因分型(Ungenotypable)，指只知道两条染色体拷贝数之和，而不知道单条染色体上的拷贝数[12].

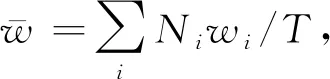
表1 变量D和一个有序变量X构成的列联表Tab.1 Contingency table generated by variable D and an ordinal variable X

(1)

它被用于Cochran-Armitage趋势检验.

1.1 可基因分型时统计量SMTTG的构建

给定一个遗传位点，记该位置上两条染色体的拷贝数为(0,0),(0,1),…,(m,n),…其中m≤n.用D代表患病状态，D=1表示患病，D=0表示未患病.假设有nA个病例和nU个健康对照，总数N=nA+nU.将数据集按照两条染色体上拷贝数组合的类别和个体的患病状态分类整理成表2，其中w=(w0,0,w0,1,…,wm,n,…)′表示趋势检验中基于模型假定对每种类别的权重赋值.

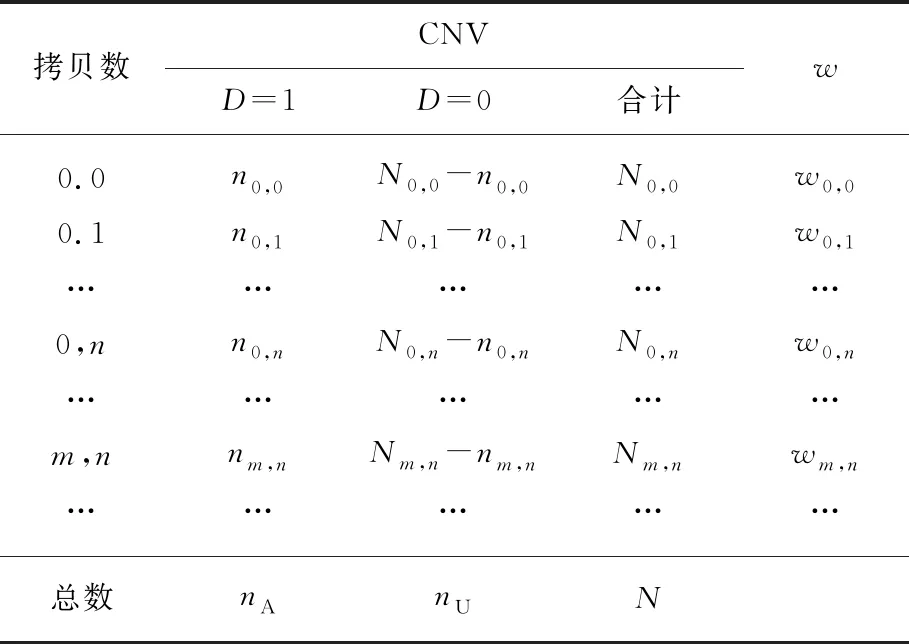
表2 按照两条染色体拷贝数组合的类别和患病状态划分而成的列联表Tab.2 Contingency table generated by the copy numbers on two chromosomes and disease status

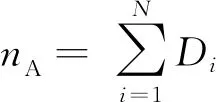
(2)

它描述了病例组与对照组在每种拷贝数类别上的平均差异.下面计算拷贝数与疾病无关联的零假设H0下，t的方差Var(t)：

(3)

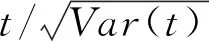
1.2 不可基因分型时统计量SMTTN的构建

由于仅有两条染色体上拷贝数之和的信息，我们把观察数据整理成如下列联表(表3).

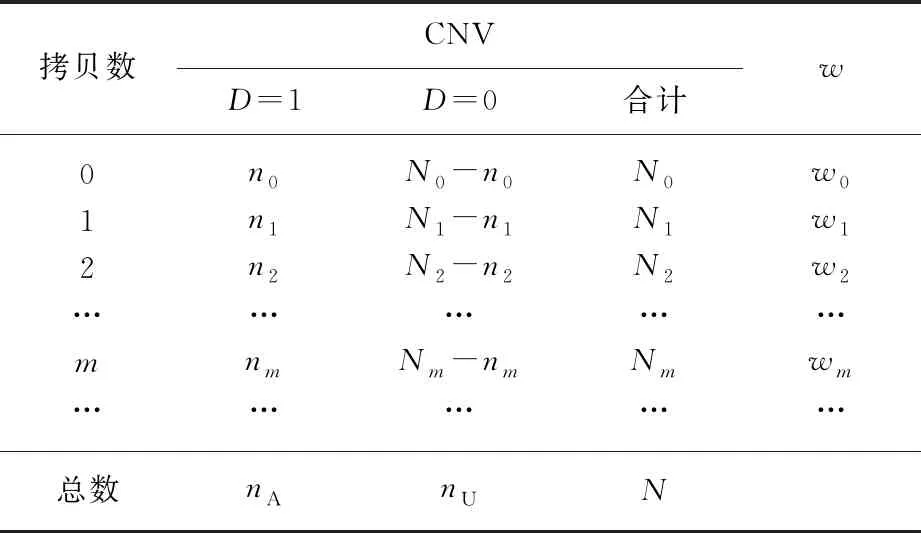
表3 按照两条染色体上拷贝数之和的类别和患病状态划分而成的列联表Tab.3 Contingency table generated by the total copy numbers on two chromosomes and disease status

给定一个遗传位点，两个拷贝数之和可取0,1,…,m,…,构建统计量的过程与前一小节类似.仍用只有一个分量是1，其余分量都是0的向量来表示个体i的拷贝数信息，Ci=(c0,c1,…,cm,…)′，即当个体i在两条染色体上的拷贝数之和为m时，cm=1，否则cm=0.类似地，得到统计量t：

t在零假设下的方差为Var(t)，它的形式已经在上一小节中给出了，但要注意的是，对于不可分型的拷贝数变异数据，其具体的计算过程有差别.在零假设下，Var(Ci)和Var(Cj)仍为一个多点分布的协方差阵.它的第1行第1列上的元为q1(1-q1)，第1行第2列的元为-q1q2，其中q1表示两条染色体上的拷贝数之和为0的概率，q2代表两条染色体上的拷贝数之和为1的概率，其余元素依此类推.协方差矩阵任意(r,c)元的计算也有相应变化.设个体X和Y的亲缘系数为(k0,2k1,k2)，他们的两条染色体的拷贝数分别用(x1,x2)和(y1,y2)表示.由表3可知，r对应于拷贝数之和r-1，c对应于拷贝数之和c-1.则需计算的(r,c)元为：

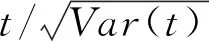
2 随机模拟研究

用随机模拟产生可基因分型和不可基因分型的两种拷贝数数据来评估检验方法MTT，并将它运用到家系数据和群体数据的检验中.

2.1 随机模拟数据的产生

先产生足够数量的初始数据集(含家系数据与群体数据)，然后根据相应的致病模型决定每个个体的患病状态.最后根据随机模拟的要求从初始数据集中筛选出符合要求的家系或病例-对照数据.它跟现实研究中样本数据的招募流程较接近.

模拟家系数据的产生：尽管MTT对家系的结构类型没有限制，但为方便起见，我们选择产生4人组家庭，每个家庭含两位父母和两位孩子.此外，还假定单条染色体上的拷贝数可以为0(缺失)，1(正常)，或2(增多)，两条染色体拷贝数的组合可以为(0,0)、(0,1)、(0,2)、(1,1)、(1,2)、(2,2)，拷贝数之和则为0～4.为使模拟数据贴近真实，采用Shao等的研究结果[19]，将单条染色体上拷贝数的概率向量设为p=(0.12,0.55,0.33)′，利用它产生父母两条染色体上(这里仅考虑常染色体)的拷贝数数据，随后由孟德尔遗传定律得到两个小孩的拷贝数.

模拟群体数据的产生：给定向量p后，不断重复产生满足上述条件的单条染色体的拷贝数，随后两两组合成一个个体的两条染色体.

患病状态的产生：考虑拷贝数变异可能的致病模型，我们采用3种不同的logistic回归模型来决定个体的患病状态.用Ca表示任意个体a的拷贝数之和，Ca1和Ca2分别表示个体a第一条和第二条染色体上的拷贝数，取β0=ln(0.1).

疾病模型1：logit[P(Di=1|Ca)]=β0+βCa.

疾病模型2：logit[P(Di=1|Ca)]=β0+β|Ca-2|.

疾病模型3：logit[P(Di=1|Ca1,Ca2)]=β0+β(I(Ca1≠1)+I(Ca2≠1)).

关于趋势检验权重的赋值，Cochran[17]认为“赋值应当体现对相应划分的构建和使用方式的最佳认识”，权重赋值事实上是一种模型假定，提供了较窄的备择假设，进而提升了统计检验的功效[17].Sasieni[20]针对基因型中的可加模型、显性模型和隐性模型，分别给予(0,1,2)、(0,1,1)和(0,0,1)3种权重赋值.我们沿用Sasieni的做法，针对上述3种疾病模型确定了3种较为简便的权重赋值.对于疾病模型1，个体a患病概率的logit值与其拷贝数之和呈线性相关，因而选择赋值(0,1,2,2,3,4)来对应两条染色体上(0,0)、(0,1)、(0,2)、(1,1)、(1,2)、(2,2)这6种类别的拷贝数组合，选择赋值(0,1,2,3,4)来对应(0,1,2,3,4)这5种类别的拷贝数之和.对于疾病模型2，|Ca-2|表示个体a拷贝数之和减去2的绝对值.当β>0时，|Ca-2|越大，患病概率的logit值也越大，因而选择赋值(2,1,0,0,1,2)来对应两条染色体上(0,0)、(0,1)、(0,2)、(1,1)、(1,2)、(2,2)这6种类别的拷贝数组合，选择赋值(2,1,0,1,2)来对应(0,1,2,3,4)这5种类别的拷贝数之和.对于疾病模型3，I为示性函数，当β>0时，单条染色体上拷贝数不等于1的个数越多，发病概率的logit值也越大，因而选择赋值(2,1,2,0,1,2)来对应两条染色体上(0,0)、(0,1)、(0,2)、(1,1)、(1,2)、(2,2)这6种类别的拷贝数组合，选择赋值(2,1,0,1,2)来对应(0,1,2,3,4)这5种类别的拷贝数之和.

2.2 随机模拟研究设计与结果

随机模拟1：在零假设下产生模拟数据，比较MTT方法P值(PMTT)与均匀分布(理论P值P理论)的吻合程度来观察其合理性.数据类型Ⅰ是家系数据，每个家庭4人，父母中一个健康一个患病，2个孩子中一个健康一个患病；数据类型Ⅱ是相关病例-不相关对照数据，其中病例组中的个体具有相关性(简便起见，我们选取患病父子对作为病例组).在这2类数据中，患病个体和健康个体人数的比例都为1∶1，且总人数定为2000，模拟研究的重复次数为1000次(以下同).图1分别展示了两种类型数据MTT方法P值与均匀分布的Q-Q图.由图可见，MTT的P值都和均匀分布吻合地很好，这表明MTT是合理可靠的.

随机模拟2：在对立假设下产生如上所述的两种类型数据.针对类型Ⅰ数据，比较MTT与CATT以及Shrestha等的GE方法[14]的功效高低.GE方法适用于基于家系的拷贝数变异数据，它考虑3人组家庭，其中父母健康孩子患病，分别比较孩子与父母的拷贝数之和.使用-1,0,1来表示孩子的拷贝数小于、等于或大于父亲(母亲)这3种情况，则每个家庭对应可以有-2,-1,0,1,2这5种赋值.对所有家庭按照赋值进行分类汇总，在拷贝数与疾病无关的零假设下，可以进行独立性的皮尔逊卡方检验.模拟结果见图2.当父子对患病时，CATT没有考虑到家庭成员的相关性，会高估方差进而使得检验统计量偏小，因而其一类错误率偏保守.MTT与GE较好控制了一类错误率.在对立假设下，针对3种疾病模型，MTT都具有更高的检验功效.针对类型Ⅱ数据，比较MTT和CATT的统计功效，模拟结果见图3(见第718页).CATT没有考虑到病例间的相关性，低估方差进而使得检验统计量偏大，导致其一类错误率偏大，因而CATT的检验结果不可靠，MTT则依然具有稳健的功效表现.

随机模拟3：传统家系数据的研究方法聚焦于一对父母和患病小孩，例如传递不平衡检验(Transmission Disequilibrium Test,TDT)[21]，FBAT(Family-Based Association Test)[22]等.这些家系中若存在健康小孩(Sibling)的信息，则通常会忽略.而使用MTT可以利用家系中健康小孩的信息来提升检验功效.为此，我们比较如下3种数据收集方案对功效的影响，方案 Ⅰ：每个家庭包含一对健康父母加一个患病小孩；方案 Ⅱ：每个家庭在方案 Ⅰ 基础上加一个健康小孩；方案 Ⅲ：每个家庭在方案 Ⅰ 基础上加一个健康人群对照.家庭数量定为500个(方案 Ⅰ 包含1500个个体，方案 Ⅱ 包含2000个个体，方案 Ⅲ 包含2000个个体).

从模拟结果图4中可以看出，方案Ⅲ表现最佳，而方案Ⅱ与方案Ⅰ相比，在功效表现上并没有多少提升，这个结果有些出乎预料.其原因可能是未患病小孩的遗传信息和两位健康父母接近(这也是有研究方法用未患病小孩信息来估计缺失的父母信息的原因之一)，因而并不能为统计量提供更多的额外信息.

随机模拟4：在随机模拟3中，我们发现在3人组家系数据的基础上多纳入一个人群对照，可以有效提升检验功效.家系数据与群体数据作为两种不同的研究对象，各有所长.因而我们自然地想到利用MTT来比较家系数据(方案A)、普通病例-对照数据(方案B)以及相关病例-不相关对照(方案C)这3种数据收集方案对统计功效的影响.方案A中，选取4人组家庭，父母和两个孩子中各有一人患病一人健康.方案B中，病例组人数与对照组人数相等.方案C中，选取患病父子对作为病例组，且与对照组人数相等.3种数据收集方案总人数都定为2000.

随机模拟结果见图5.在各种情形下，方案C都具有更高的相对功效，方案B的功效次之，而方案A的功效较前两者低一些.其原因可能是在家系数据中，患病个体和未患病个体通常具有血缘关系，导致遗传信息相似，这在流行病学中称为“过度匹配(Overmatching)”[23]现象.因而在不考虑人群分层等混杂因素的情况下，我们可以优先考虑基于群体数据的采集方案以获得更高的检验功效.

综上，当研究对象中包含相关个体时，MTT方法能在控制住一类错误率的前提下，拥有较好的功效表现.而借助具有更广适用范围的MTT方法，我们比较了多种数据采集方案的功效表现，这给数据采集策略提供了一定的参考.

3 真实数据分析

我们选取了来自机构SFARI(Simons Foundation Autism Research Initiative,https：∥www.sfari.org/)下的一个项目Simons Simplex Collection(SSC)的研究数据.SFARI成立于2003年，致力于孤独症谱系障碍的研究，SSC作为SFARI旗下的一个核心研究项目，目前已招募了超过2700组家庭，这些家庭大多为4人组家庭，每个家庭有一个患有孤独症谱系障碍的孩子(Proband)，2个健康的父母(Parents)以及一个健康的兄弟姐妹(Sibling).本次分析的数据中共包含1710个父母、836个患病的孩子和834个健康的孩子.原始拷贝数变异数据来源于比较基因组杂交芯片平台，经过处理后得到的信息为两条染色体上拷贝数之和，故采用SMTTN统计量.

根据数据库提供的背景信息，在数据集的所有个体中，共检测到了980个发生了拷贝数变异的位点，去除X染色体上的位点后，共有930个常染色体上的拷贝数变异位点.拷贝数变异的范围是0～4，其中0和1为缺失，2为正常，3和4为增多.针对拷贝数之和为(0,1,2,3,4)这5种类别，根据拷贝数变异与孤独症谱系障碍之间可能的背景机制[24-25]，选取(2,1,0,1,2)作为统计量的权重赋值.针对这930个常染色体上的拷贝数变异位点，运用MTT、CATT和GE进行统计检验.

图6展示了MTT的检验结果，经多重校正后，共有26个具有显著性意义的拷贝数变异位点.使用CATT和GE则分别检验出了19个和17个具有显著性意义的位点.针对MTT、CATT和GE检测出的显著性位点，我们利用DGV(Database of Genomic Variants,http：∥dgv.tcag.ca/dgv/app/home)与NCBI Data Viewer(https：∥www.ncbi.nlm.nih.gov/genome/gdv/)网站搜集并整理了这些拷贝数变异位点上所对应的基因.结果如图7所示.对于MTT检测所得的26个拷贝数变异位点，共整理得到242个基因.对于CATT和GE检测得到的拷贝数变异位点，分别整理得到161个和133个基因，图7中的公共部分表示其中重合的数量.在检测得到的显著性位点数与基因的数量上，MTT都要多于CATT和GE，且CATT的检测结果大部分都包含于MTT的检测结果中.

针对MTT检测得到的显著性位点所对应的基因，我们利用GeneAnalytics网站(https：∥geneanalytics.genecards.org/)对上述基因进行功能富集分析，并通过文献检索来进一步了解这些基因背后可能包含的生物学意义.图8展示了利用MTT检测到的基因中富集水平前7位的身体组织与生理系统.由图8(见第720页)可见，在身体组织中得分最高的是大脑.而在生理系统中得分最高的则是神经系统.图8中组织与系统的得分是由匹配到的基因得分计算而来，得分越高表明关联性越强，而基因得分则取决于其所对应的实体类型和基因注释.已有的研究结果表明，孤独症谱系障碍的发病与大脑[26]和神经系统[27]息息相关，这在一定程度上表明了MTT找到的基因与孤独症谱系障碍之间的关联性.

图9展示了富集水平前7位的生物学过程(GO Term)与通路，其中条状图右侧的数字表示匹配的基因数量.在GO Term生物学过程中富集水平排前5类的分别是肌细胞分化正调控，甘油磷脂合成过程、维生素E细胞应答、甾类激素应答和输卵管发育.Wu等[28]研究发现杜氏肌营养不良与孤独症共同发生的几率要显著高于随机水平，但是目前导致两种疾病相关联背后的生物学机制仍有待研究.Chauhan等[29]比较了孤独症患儿与健康儿童的氨基-甘油磷脂水平，结果表明：孤独症患儿的磷脂酰乙醇胺水平较低而磷脂酰丝氨酸水平较高.基于此特征，研究人员认为可以将氨基-甘油磷脂水平作为诊断孤独症的一种生化指标.Amminger等[30]在进行的一项双盲试验中表明：给孤独症患儿补充服用Omega-3脂肪酸可以缓解并改善病症，而维生素E作为一种有效的抗氧化剂，在本研究中与不饱和脂肪酸共同服用以减少自由基的影响.Auyeung等[31]总结并发现产前的甾类激素暴露会明显增加孤独症的患病几率.

在通路富集分析的结果中，排前5的分别是成肌过程中的CDO信号通路、早老素调节信号通路、嘧啶脱氧核糖核苷酸降解通路、G12～G13细胞信号通路和ESR1与ESR2基因非配体依赖性激活通路.Fatemi[32]发现带有早老素-1缺陷的小鼠存在大脑皮层的发育异常，后续研究表明早老素-1缺陷与颤蛋白突变有关.而在精神分裂、孤独症、无脑回畸形等患病人群中都发现有颤蛋白突变现象，可能的原因是颤蛋白突变所导致的大脑内部结构的变化.Herman等[33]总结了一些可能导致孤独症的病因，其中有部分报道案例即是由嘧啶代谢异常所引起的.Wang等[34]的研究表明ESR1基因的多态性与ESR2基因的超甲基化都与孤独症的发生有着紧密的关联.此外，我们还检索了MTTu检测到的相关功能注释基因的文献.Quinlivan等[35]跟踪研究了3例带有CHKB基因突变的肌肉萎缩症病人，其中的一例病人在7岁时被确诊为孤独症谱系障碍.Wei等[36]对孤独症小鼠大脑皮层组织进行了蛋白质组分析，结果表明在孤独症小鼠中CPNE7基因的表达显著上调，因而可能是导致孤独症的候选基因之一.Bhalla等[37]利用队列研究，发现CDH15和KIRREL3基因上的非同义突变可能会导致不同程度的智力障碍.多项研究表明CTNNB1基因上的突变与智力障碍及孤独症谱系障碍等疾病相关，Dong等[38]在小鼠中敲除了CTNNB1基因来研究其可能的致病机理，结果发现基因敲除小鼠表现出明显的目标识别与社交互动上的障碍，并重复相同动作，这与人类孤独症的症状相似.进一步研究发现c-Fos基因在这些小鼠大脑皮层中的表达量显著降低而在其他组织中的表达量保持正常.该研究揭示了CTNNB1上的突变可能会导致c-Fos基因发生组织特异性的表达变化，进而可能导致孤独症相关的症状.Uchino等[39]研究发现SHANK3基因表达量的下降与孤独症之间存在明显相关性.进一步研究表明，DNA甲基化可以组织特异性地调控SHANK3基因的表达量，进而影响到神经突触的发育、成熟和稳定.值得注意的是，在上述基因中，CHKB、CPNE7和SHANK3仅包含在MTT的检测结果中.由此可见，MTT相较其他两种方法能找到更多的拷贝数变异位点，且这些位点上的基因与孤独症谱系障碍确实存在着一定的关联性.

4 总结与展望

作为人类基因组遗传多样性中的重要组成部分，拷贝数变异已经成为了遗传学、生物医学等领域重要的研究对象之一.拷贝数变异的产生机制、与疾病之间的潜在关联也随着人类的不断研究而慢慢揭开面纱.同时随着测序技术的不断进步以及各种基于测序的人类基因组研究项目的推进，每天都在产生着大量的测序数据.目前针对拷贝数变异的研究方法多数着重于如何基于测序数据进行检测和定位.而针对拷贝数变异与疾病的关联分析的方法依然甚少.针对现有方法存在的一些局限性，以及经过处理后的拷贝数变异数据的特点，在传统的Cochran-Armitage趋势检验的基础上，我们提出MTT方法，它适用于相关个体拷贝数变异数据.拷贝数变异数据可以是可基因分型和不可基因分型.通过随机模拟，我们检验了MTT的可靠性，并在多个场合与已有方法做了功效的比较，结果表明MTT方法具有更高的灵敏度.此外还比较了不同的数据采集方案下MTT统计量的相对功效，结果表明以相关病例-不相关对照作为研究对象的数据采集方案具有更好的功效表现.随机模拟结果体现了MTT具有较广的适用范围，且随机模拟的结论对数据采集方案也有一定的指引意义.在实际数据分析中，我们运用MTT方法处理了SSC数据，得到了26个具有显著性的拷贝数变异位点，我们整理了这些拷贝数变异位点上对应的基因，并通过功能富集分析和文献检索，进一步展示了这些基因与孤独症谱系障碍可能的关联，并为后续的实验研究提供了一定的指引.

MTT方法仍有几点值得注意与改进的地方：(1) MTT方法基于趋势检验，因而依赖一定的模型假定，模型假定提供了较窄的备择假设与更高的检验效能.在实际数据分析中，需要借助一定的背景知识或先验信息来确定疾病模型.若缺少有助于确定模型的背景知识或先验信息，导致模型对现实的描述不符，则此时的检验效能将会下降，皮尔逊卡方和似然比检验会是更为可靠的检验方法.(2) 针对给定的遗传模型，能否确定一个趋势检验的权重赋值，使得在一定水平的相对功效下所需的样本数量最小(即是否能选择到最优的权重赋值)？Zheng等[40]研究了给定基因遗传模型下的最佳赋值问题.他们使用极坐标和一个表示角度的参数θ来描述可加、显性和隐性3种遗传模型，进而将最优赋值问题转化为带参数θ的极值问题，这无疑对基于拷贝数变异数据的最优赋值问题提供了解决思路.如果能将拷贝数变异的遗传模型也转化为仅有一个参数的模型，那么或许也能找到给定遗传模型下适用于拷贝数变异数据的最优赋值.(3) MTT 方法所针对的是单个拷贝数变异位点，对于复杂疾病，单个拷贝数变异位点能解释的遗传方差往往有限，因而如何在统计量中将多个拷贝数变异位点的信息结合起来，提出一个针对多位点的检验统计量是今后针对拷贝数变异与复杂疾病的关联研究的方向之一.