基于城市轨道交通大数据的站点客流存量反演与客流去向预测
刘 婵,黄天印,江 渝
(1.复旦大学 数学科学学院,上海 200433;2.上海申通地铁集团有限公司,上海 201103;3.上海财经大学 数学学院,上海 200433)
随着我国城市规模不断扩大和经济建设飞速的发展,城市化进程在逐步加快.以轨道交通为骨干的公共交通体系在为城市居民提供安全、快速、舒适的交通环境的同时,也成为了解决大城市交通拥堵、环境污染问题的主要途径.近几年国内城市轨道交通行业实现超常规高速发展,预计到2020年年底全国拥有轨道交通的城市将达到50个,总通车里程将达到近6000km,总投资将达4万亿元的规模.截至2018年12月,上海市城市轨道交通路网共有415个站点,里程长达673km,几乎覆盖了整个城市,运营里程已经跻身世界第一.轨道交通路网规模日益庞大、结构日益复杂,对路网的安全运营管理提出了一个极大的挑战.利用轨道交通进出站大数据,实时掌握路网中各个站点的客流存量和各条线路上的客流负载信息,及时准确地对路网超负载的可能位置和时间作出预警,进而通过限流、调整行车间隔等手段有效控制引导客流,从而有效防控事故风险、提高乘客乘车舒适度,是路网精细化管理中最重要的课题.
该问题的数学建模与算法主要是在每个乘客都选择最短出行路径的假设下(参见文献[1]),利用乘客进出任意两个站点的公共交通卡记录数据来实现.特别需要解决如何通过大数据将客流量分配到各条最短路径上,从而准确反演各个站点的实时客流存量和有效预测客流去向.文献[2-11]讨论了用于确定最短出行路径的K短路搜索算法和Dial算法,以及计算客流去向分配比率的Logit模型等.虽然这些算法都很有效,但模型中多设定了诸多变量并通过日常问卷产生的数据来进行计算,还没有能够充分利用现有的交通卡进出站大数据来进行反演或者预测的研究.
本文利用图论中交通/流量网络的概念对轨道交通路网进行了拓扑建模,对各个站点通过闸机进/出站客流量和通过线路到达/离开客流建立了客流守恒公式.基于该守恒公式和大数据机器学习算法对路网每个站点进出站数据进行分析和挖掘,得到了将路网客流量“分配”到每对进出站点间K条最短路径上的比率,进而建立了反演各个站点客流存量和对线路客流负载进行预测的数值算法.
1 反演预测模型和算法的建立
我们利用图论对研究的实际问题建立相应的数学模型.
1.1 交通/流量网络
上海轨道交通的部分路网结构如图1(a)所示.根据这个路网结构我们可以用图论建立交通网络/流量网络(参见文献[12]),即建立如图1(b)所示的有向图G=(S,s,t,E).这里:(S,s,t)是顶点集;S是模拟M个现实站点S1,S2,…,SM的集合;s是流量只出不进的虚拟顶点即源点(source)s1,s2,…,sM组成的集合;t是流量只进不出的虚拟顶点即汇点(sink)t1,t2,…,tM组成的集合;E是边集.
由于有3类顶点,在边集E的边上定义3类流量函数:
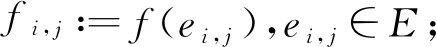
2) 从源点si进入站点Si(i=1,2,…,M)的进站(客)流量函数Ii;
3) 从站点Si进入汇点ti(i=1,2,…,M)的出站(客)流量函数Oi.
同时,可以定义边集E的任一条边上的容量函数(即最大流量函数)为c(e)(∀e∈E).显然这里的流量函数fi,j(或Ii,Oi)和容量函数c(e)与时间相关.在固定时刻t,应该满足以下两个条件:
1) 容量限制(Capacity constraints):每条边e上的流量函数fi,j(或Ii,Oi)≤c(e);
2) (客)流守恒(Flow conservation):对于每个站点Si,t时刻前后流量函数满足:
(1)
式(1)等号左(或右)边值即为站点Si在t时刻的客流存量,记为Ci(t).客流存量的概念在轨道交通网络管理决策中扮演了重要角色.一方面,它衡量了轨道交通路网的承载能力;另一方面,它可以反映轨道交通网络的繁忙程度,从而为轨道交通限流等举措提供参考.
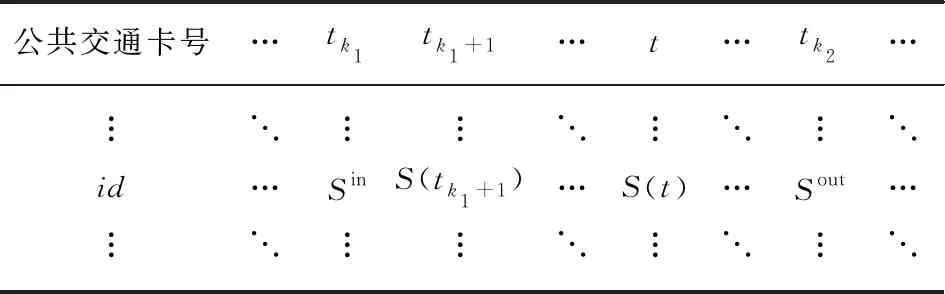
正确反演实时客流存量Ci(t)是本文需要解决的主要问题.从监测和实时记录的角度看,轨道交通网络中可以获取的数据非常有限.可能获得的原始数据主要是乘客出入站点使用公共交通卡的记录,每条记录可以包含的信息仅为:卡号、每次轨道交通出行的金额、进出的站点及相应时间(如表1所示).但是由于上海轨道交通除个别站点外实行的是“不出站换乘”,将进出站数据应用到式(1)中也只能确定Ii(t)和Oi(t),无法确定fi,j或者fj,i的信息.

表1 公共交通卡出入站记录Tab.1 Public transport card entry and exit records
1.2 离散时间表示
但是当我们对时间作离散化,并考虑如下假设:
假设1为描述轨道交通网络中客流流动过程,假设:
1) 所有轨道交通线路上所有轨道交通的发车间隔、运行速度均相同,并记发车间隔为Δt;
3)t0 4) 初始时刻记为t0,结束运营的时间记为tN+1; 5) 相邻站点间距离相同,列车行驶需要耗时Δt,即假设以相邻站点距离中点为界,即使乘客在列车上,也等同于在两个站点中的一个站点上; 6) 忽略轨道交通到达站点与再次发车的时间间隔; 7) 时间段[tj-1,tj)进站的客流必将搭上tj时刻到站的轨道交通; 8) 同站换乘耗时Δt; 9) 时间段[tj-1,tj)从相邻站点坐车抵达的出站乘客,在tj时刻出站,[t0,t1]内没有出站乘客; 10) 站点间线路客流量的最大承载量为无穷大,进站出站的最大客流限制也是无穷大,即容量函数. c(e)≡∞ ∀e∈E. 表2 离散时间下单个乘客的乘车轨迹Tab.2 The track of a single passenger in discrete time 这样,时间段(tk-1,tk]内站点Si聚集的客流有两个来源:一个是该时间段内通过闸机进入Si的;另一个是搭乘列车在tk到达(或途经)站点Si的客流.同样地,该站点下个时间段(tk,tk+1]的客流去向包括tk+1时刻通过闸机从Si出站的,以及搭乘tk+1时刻到站的轨道交通前往邻接站点的.根据表2,tk时刻各个流量函数可以表示按乘客卡号进行加和: (2) 这里δx,y={1(x=y),或0(x≠y)}是Kronecker函数.记tk时刻前刚进站的乘客数量为a,此刻刚随车到达并出站的乘客数量为c,仅在此刻途径Si站、不是刚进站也不是要出站的乘客数量为b,则易知Ii(tk)=a,Oi(tk+1)=c, 流量函数能满足客流守恒式(1),且相应的客流存量为 (3) 从式(3)可以看到,如果我们由单个乘客数据(id,Sin,Sout,tk1,tk2)可以重构出乘车轨迹表2的话,那么就可以计算出流量函数(2),从而得到tk时刻的客流存量: 这就是我们需要解决的问题1:客流存量反演问题. 单纯根据单个乘客的离散数据DAid来具体确定该乘客选择的具体路线几乎是不可能的.但是,尽管每个人的情况千差万别,存在诸如坐过站、坐错车等情况,乘客选择路线基本上还是基于路线长度、换乘时间和线路的拥堵程度等因素.通过基于概率统计的大数据分析技术,对某类乘客的大概率行为进行分析,考察该类乘客在固定站点区间上的路线选择分布,而不是考察单个乘客的路线选择,这为我们解决问题提供了思路,即我们对单个乘客数据(id,Sin,Sout,tk1,tk2)按照相同出入站点和相同进站时刻(Sin,Sout,tk1)进行分组,则对于每个离散时刻tk(k=0,1,…,N+1),存在sk组数据: 其中:sf指在tk时刻在Sin站点进站乘车且有相同终点站Sout的乘客数量.注意到sk≤M×M,即分组数据的组数不超过进出站(Sin,Sout)组合数的总数,因此矩阵ODk的维数是有限的. 由于每组分组数据(sf,Sin,Sout)可选的线路总是有限的,假设途经站点一样但出站时刻不同的线路定义为不同路线,有fΓ位乘客选择了路线Γ,每个乘客的线路轨迹可记为多元函数Γ: 其中:SΓ(t)是t时刻该路线乘客途经的站点.注意到在进出站时间段(tk1,tk2)以外的时刻,乘客途经站点设为0,即 (4) 说明1这个Γ包括所有不同起点-终点但都经过站点Si的线路. 这样估计选择各条路线Γ的客流人数fΓ是非常重要的,特别需要给定如下假设: 假设2给定起始站和终点站,1) 忽略实际中的特殊情况,如坐过站;2) 乘客倾向于用时少、少换乘的线路. 此外,利用式(3)预测tk+1时刻出站客流Oi与去往邻接站点的客流fi,j是需要解决的问题2:客流去向预测问题.这里我们重新定义: 综上所述,本文中需要解决的问题如下: 根据前述讨论,我们给出客流重构算法如下: 1) 对于每个时刻tk,统计分组数据ODk; 2) 对于每一条分组数据,即矩阵ODk中的每一行,即(sf,Sin,Sout),计算站点Sin与站点Sout之间的前K条最短路径; 4) 由式(4)计算轨道交通交通流Ii(tk)和fj,i(tk); 5) 由式(3)计算客流存量Ci(tk). 说明2对该重构算法有具体说明如下: 1) 我们采用了贪心算法(Greedy algorithm)计算任意两个站点Si与Sj之间的前K条最短路径[12]; 这里我们利用上海轨道交通路网数据对前述的客流存量反演与客流去向预测问题进行数值测试. 来进行算法的误差分析,即定义 为站点Si在tk+1时刻的出站量误差. 根据客流重构算法和说明2,我们利用2018年上半年上海轨道交通的“OD”表数据进行测试: 1) 路线数K=3(K最短路径算法一般假设K≤3,参见文献[6]); 2)大数据分析得到倾向度(即线路选择概率):(p1,p2,p3)=(0.7,0.2,0.1). 反演得到的出站客流量如图2所示,出站量误差如图3所示.由图可以看到:出站客流量大,即有效样本量大能够有效提高反演的准确度. 图4给出了反演得到的某工作日上海最重要的几个轨道交通站点客流存量的变化.存量绝对数值符合站点情况,时间方向的峰值也对应早晚上下班高峰时间.气泡图图5反映的是反演得到的全路网各站点的日均客流存量,反演的数值与实际情况相符.我们可以更直观地看到图4中各站点的客流存量大小与其周边轨道交通结构网的关系,当然我们还可以绘制各个时刻各个站点的客流存量气泡图,并由此推断客流分布的流向.这充分说明了客流存量这一指标在轨道交通运营管理中的重要作用. 致谢:感谢复旦大学数学科学学院研究生李玮、刘小满对本工作的帮助.感谢上海申通地铁集团有限公司信息中心的数据支持,以及上海久誉软件系统有限公司的大力协助.
1.3 基于公共交通卡数据的客流存量反演与客流去向预测


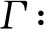


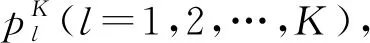

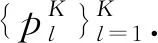
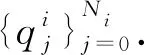
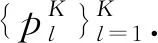
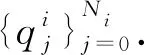
1.4 反演预测算法
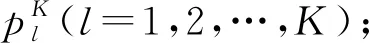
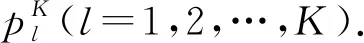

2 数值测试
2.1 客流存量反演

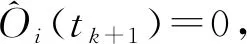
2.2 客流去向预测


