一个三角形几何不等式的推广

单佳骊， 楼红卫

(1.复旦大学 >附属中学，上海200433； 2.复旦大学 >数学科学学院，上海200433)

1 引 言

在几何不等式研究中，三角形几何不等式的研究占有重要地位.一些三角形几何不等式非常简洁优美，证明思路通常利用余弦定理等三角函数性质去证，解法简单快捷.如下是第3届国际数学奥林匹克IMO竞赛题中一个三角形几何不等式及其解法.

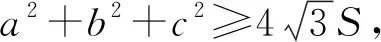
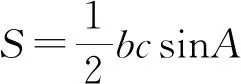
又由Cauchy不等式知b2+c2≥2bc，再结合sin(A+π/6)≤1，得到

且等式成立当且仅当a=b=c(即当且仅当b=c且A=π/3).证毕.

上述解法巧妙地运用了三角形中各边长和面积与三角函数之间的关系，再结合Cauchy不等式而快速得到原命题.受命题1启发，有两个问题值得我们思考和研究：

(i) 能否将命题1中的三角形几何不等式推广为更一般的三角形几何不等式？

(ii) 能否将命题1中的三角形几何不等式推广为多边形几何不等式？

有很多文献研究了三角形几何等式和不等式乃至多边形几何等式与不等式，例如文献 [1-2]研究了三角形几何等式、不等式及其推广，文献[3-4]研究了圆外切和圆内接多边形几何不等式.本文将利用凸函数的Jensen不等式[5]，将几何问题转化为代数问题，获得比命题1更具一般性的三角形几何不等式(见第2节推广1)和圆外切多边形几何不等式(见第二节推广2).

2 主要结论及其证明

首先，将命题1的三角形几何不等式推广到更一般的三角形几何不等式.

推广1设a,b,c为某个三角形的各边长，S为其面积.则对任意大于1的实数α，有

aα+bα+cα≥2α31-α/4Sα/2,

其中等式成立当且仅当a=b=c.

其次，将命题1由三角形情形推广到更一般的圆外切多边形情形.

推广2对于n≥3, 设a1,a2,…,an为某个圆外切多边形的各边长，S为其面积.则对任意大于1的实数α，有

其中等式成立当且仅当a1=a2=…=an.

接下来,结合Jensen不等式，将把推广1和2这两个几何问题转化成代数问题，这将大大简化证明过程.先给出二个重要引理：

引理1令x1,x2,…,xn为正数，n≥1.则对任意不小于1的正数α，有

证令f(x)=xα,x∈(0,+∞),则f″(x)=α(α-1)xα-2>0,x∈(0,+∞).因此f是(0,+∞)上的凸函数.由凸函数的Jensen不等式知：当x1,x2,…,xn>0时，有

即

其中等式成立当且仅当x1=x2=…=xn.证毕.

引理2设n≥1，实数x1,x2,…,xn∈(0,π/2).则

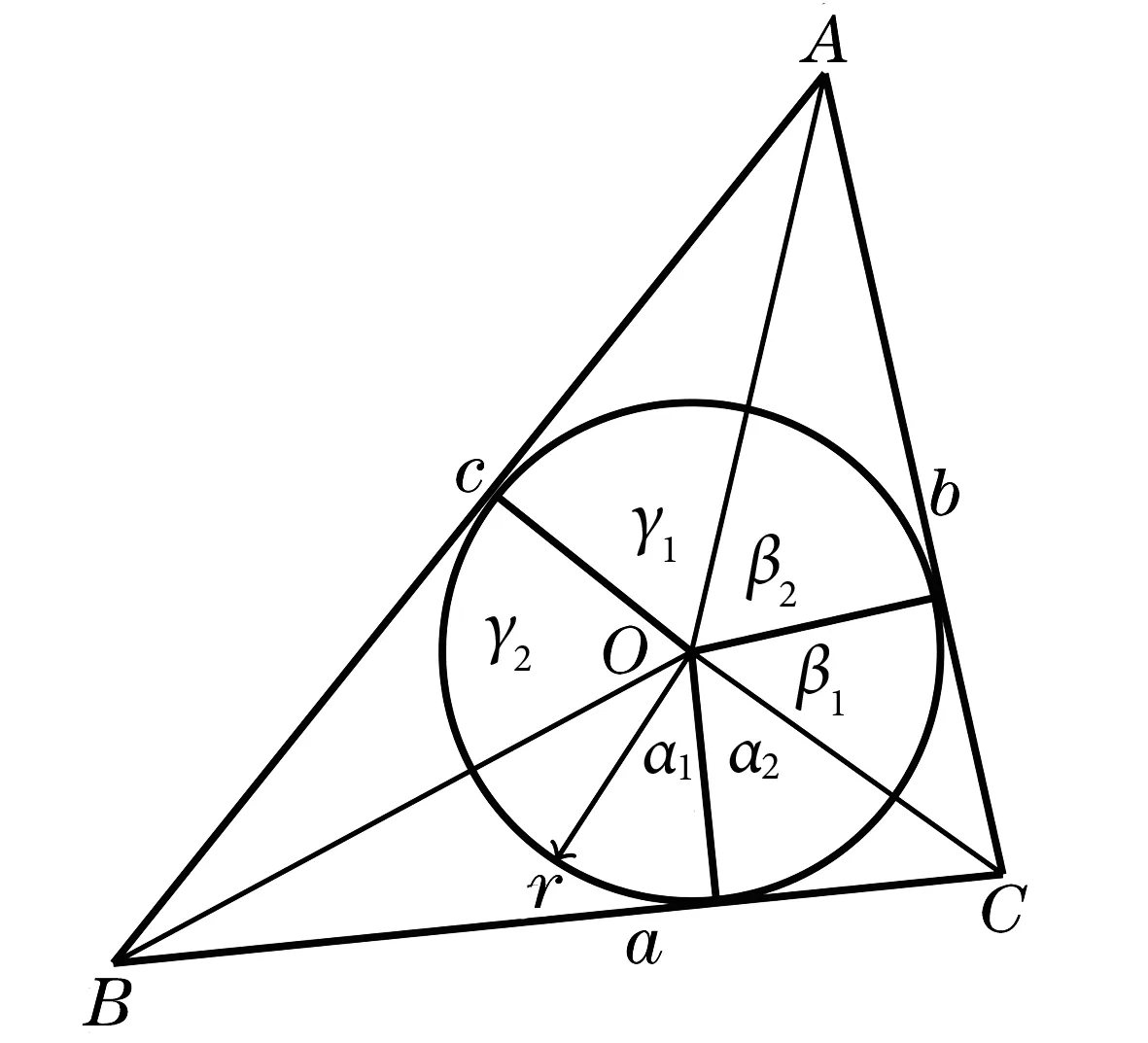
图1

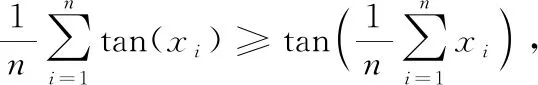
其中等式成立当且仅当x1=x2=…=xn.

证取f(x)=tanx，其中x∈(0,π/2).则f″(x)=2sinx(cosx)-3>0,x∈(0,π/2).因此f是(0,π/2)中的凸函数.由凸函数的Jensen不等式知

选取定级因素因子体系和确定其权重是耕地定级关键的一步。考虑到耕地的自然、社会、经济与区位属性，需要选取的评价因素因子较多，计算量较大，利用GIS对空间信息强大的采集、存储、分析、管理能力是耕地定级及对成果进行科学管理的有效途径[12-16]。

即

其中等式成立当且仅当x1=x2=…=xn.证毕.

下面给出推广1和2的证明.

推广1 证设ΔABC的内切圆圆心为O，半径为r(见图1)，则

从而有

故

a+b+c=r[(tanα1+tanα2)+(tanβ1+tanβ2)+(tanγ1+tanγ2)]，

由于α1,α2,β1,β2,γ1,γ2∈(0,π/2)，应用引理2得

所以

(a+b+c)2=r2(tanα1+tanα2+tanβ1+tanβ2+tanγ1+tanγ2)2

=2S(tanα1+tanα2+tanβ1+tanβ2+tanγ1+tanγ2)

即

其中等号成立当且仅当α1=α2=β1=β2=γ1=γ2=π/3，即a=b=c.又由引理1知

(aα+bα+cα)/3≥3-α(a+b+c)α，

故

其中等式成立当且仅当a=b=c.证毕.

推广2 证设正整数n≥3，n边形的顶点依次为A1,A2,…,An，边长依次为a1,a2,…,an，内切圆圆心为O，半径为r，各边所对的两个内顶角分别为β2i-1,β2i(1≤i≤n).则类似推广1的证明，有

由引理2知

所以有

即

a1+a2+…+an≥(4nStan(π/n))1/2,

且等号成立当且仅当β1=β2=…=β2n=tan(π/n)，即a1=a2=…=an.

再由引理1知，对任意大于1的实数α，

从而我们有

其中等式成立当且仅当a1=a2=…=an.证毕.

3 结 语

本文从一个三角形几何不等式出发，利用凸函数的Jensen不等式，把几何不等式问题转化到代数不等式的证明，证明思路简洁快捷，并获得了更一般的三角形几何不等式及圆外切多边形几何不等式.类似问题对于提升高中阶段的学生学习数学的兴趣和进行初步的研究有很大帮助.

致谢感谢复旦大学“步青”高中生学术见习计划，感谢参考文献给予我们的启发.