诣零换位子中心环的一些刻画

邵雨凡， 陈建华， 魏俊潮

(扬州大学 >数学科学学院，江苏 >扬州225002)

1 引 言

环的交换性的众多条件，优美且有对称性，但经过时代的发展，环论学者发现研究的环的交换性条件过于复杂，或是失去了创新性.随着探究的深入，在近十年来，环论学者将重点转移到局部化的半交换性问题上，如文献[1-3]中所研究的CN环、JTTC环和拟正规环等，探究这些环的性质并利用这些环刻画一些经典的环类，更宽泛地诠释了半交换性问题所具有的意义与价值.本文基于对幂零元素及幂等元素的探究，主要研究在局部交换性条件下环所呈现的性质，给出诣零换位子中心环的若干性质和刻画，其价值在于研究的结合环的半交换性问题保持了环的交换性的若干性质，但条件的放宽意味着适合更多的环类，同时应用性也得到增强.

本文中，R表示有单位元的结合环、N(R)表示R的全体幂零元的集合、Z(R)表示R的中心、E(R)表示R的全体幂等元集合.

定义1[4-6]若对任意a∈N(R)，x∈R，总有[a，x]∈Z(R)，其中环上两个元素a与x的交换子定义为[a，x]=ax-xa，则称R为诣零换位子中心环，简称NC环.若E(R)⊆Z(R)，则称R为Abel环.若N(R)={0}，则称R为约化环.若对任意a∈R，当aRa={0}，总有a=0，则称R为半素环.设I是R的理想，若I中的每个元素都是R的幂零元素，则称I是R的诣零理想；若N(R)∩I={0}，则称I为R的约化理想.若对任意x，y∈R，总有[x，y]∈Z(R)，则称R为换位子交换环.

显然交换环总是换位子交换环，但由文献[7]知，换位子交换环未必为交换环，除非R为半素环.换位子交换环当然是NC环.

定义2[8]设a∈R，若存在b∈R，使得a=aba，则称a是R的正则元；若存在b，c∈R，使得a=a2b=ca2，则称a是R的强正则元.

定义3[9-10]设a∈R，若存在b∈R，使得a=aba，b=bab，ab=ba，则称a为R的群可逆元，且称b为a的群逆元，通常记为a#.用R#表示R的全体群可逆元的集合.

定义4[11]设*∶R→R为双射，满足条件：

(a*)*=a， (a+b)*=a*+b*， (ab)*=b*a*，

则称R为卷积环或*-环.设R为*-环，a∈R，若存在c∈R，使得

a=aca，c=cac， (ac)*=ac， (ca)*=ca，

则称a为Moore Penrose可逆元，简称MP可逆元，且称c为a的MP逆元，记为a+.用R+表示R的全体MP可逆元的集合.设a∈R#∩R+，若a#=a+，则称a为R的EP元.用REP表示R的全体EP元的集合.

2 主要结果

NC环是一类特殊的结合环，下面通过研究NC环与多种环之间的联系，给出NC环的性质和刻画.命题1指出NC环实际上也是Abel环.

命题1NC环为Abel环.

证设R为NC环.任取e∈E(R)，任取a∈R，记h1=(1-e)ae，h2=ea(1-e)，则

h1e=h1，eh1=0=h2e，h2=eh2，

而

注意到

[h1，e]=h1e-eh1=h1-0=h1， [h2，e]=h2e-eh2=0-h2=-h2，

所以h1，h2∈Z(R)，从而

h1=h1e=eh1=0，h2=eh2=h2e=0.

因此对每个a∈R，ae=eae=ea，从而e∈Z(R)，故R为Abel环.

注1 命题1的逆命题不成立：

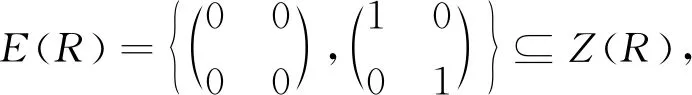
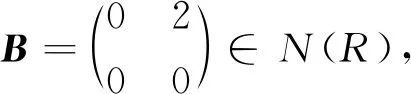
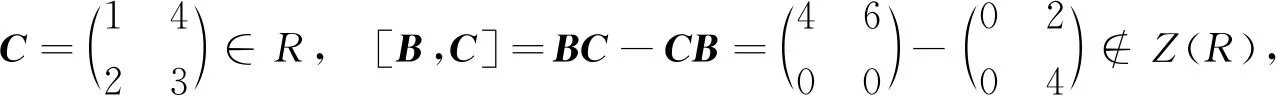
故R不为NC环.

设

则根据通常的矩阵加法及乘法，WT3(R)成为一个环. 借助于NC环，下面的命题给出了交换环的一个刻画.

命题2R为交换环当且仅当WT3(R)是NC环.

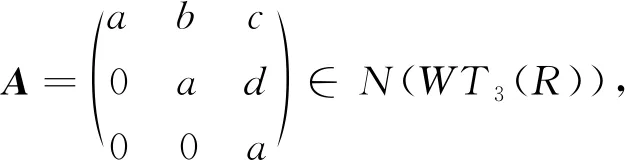
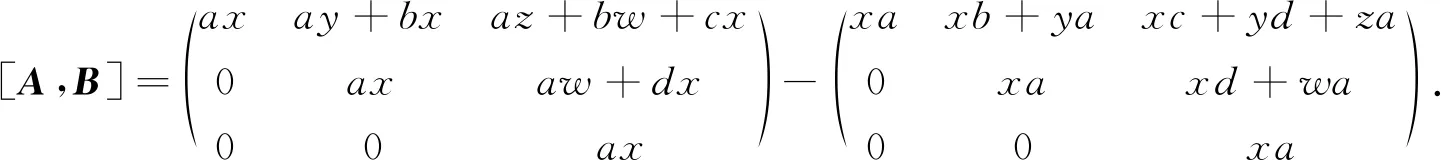
由于R为交换环，故

于是WT3(R)是NC环.

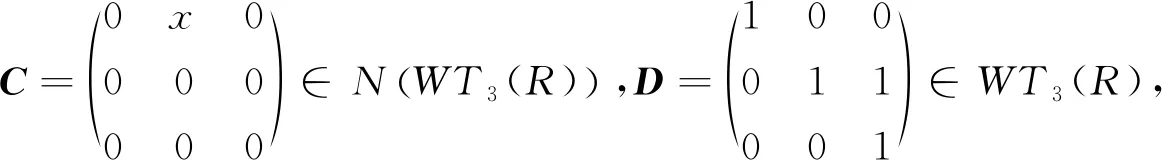
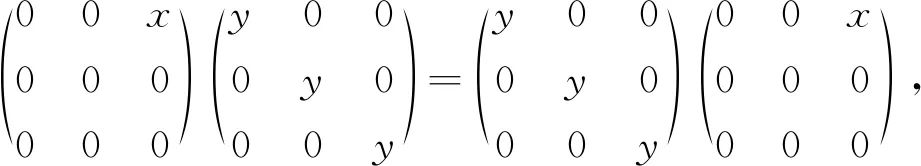
即

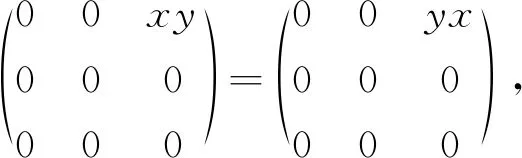
所以xy=yx，于是R为交换环.

设

则根据通常的矩阵加法及乘法，V2(R)成为一个环.

命题3设R为交换环，则V2(R)为NC环.

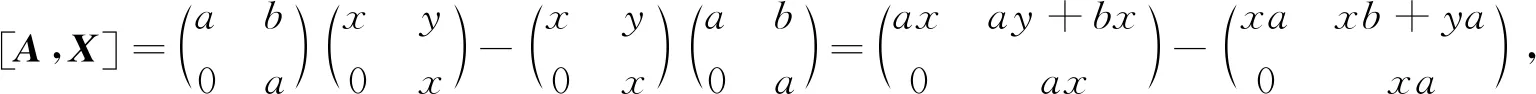
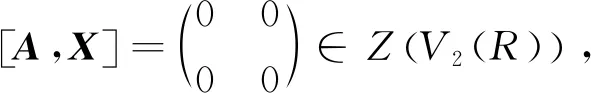
注2 命题3的逆命题不成立，即当V2(R)为NC环时，R不必为交换环：设F是一个域，当取

为NC环时，R不是交换环.

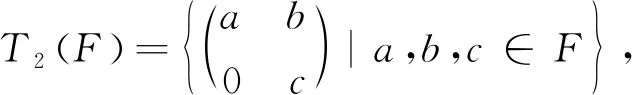
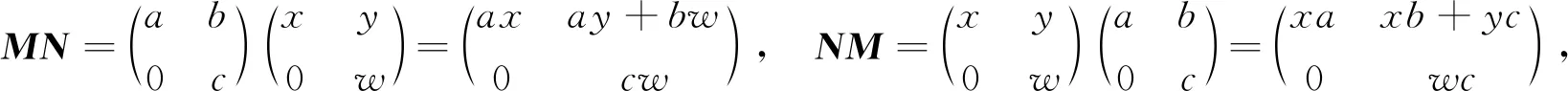
MN≠NM，所以R不是交换环.

下面利用环同构建立NC环、半素环以及交换环之间的联系.

命题4设R为半素环，若V2(R)为NC环，则R为交换环.

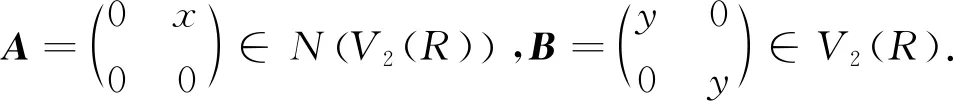
从而对任意的z∈R，(xy-yx)z=z(xy-yx)成立，因此xy-yx∈Z(R).由文献[7]中定理1知R为交换环.

设R为半素环，记T(R，R)={(a，b)|a，b∈R}，在T(R，R)中定义加法及乘法如下：

(a，b)+(x，y)=(a+x，b+y); (a，b)(x，y)=(ax，ay+bx)，

则T(R，R)为一个环.

推论1设R为半素环，若T(R，R)为NC环，则R为交换环.

·

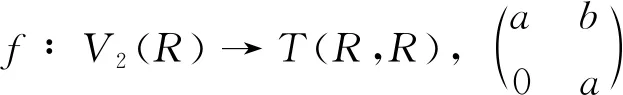
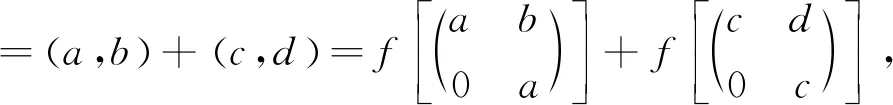
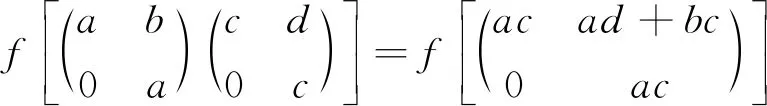
所以f是同态映射.因为对任意的a，b，c，d∈R，a=c与b=d不同时成立.

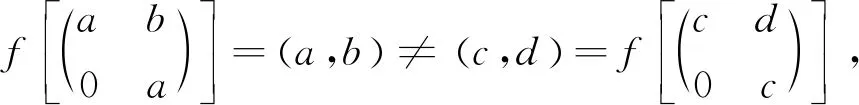
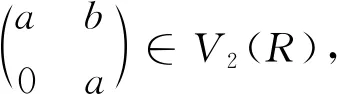
设x是一个未定元，记R[x]为R上的一元多项式环，记(x)表示由x生成的理想，则有商环R[x]/(x2)，记为R〈x〉.容易看出R〈x〉={a+bx|a，b∈R，x2=0}，定义R〈x〉中加法及乘法如下：

(a+bx)+(c+dx)=(a+c)+(b+d)x； (a+bx)(c+dx)=ac+(bc+ad)x，

则R〈x〉为一个环.

推论2设R为半素环，若R〈x〉为NC环，则R为交换环.

证构造映射g∶T(R，R)→R〈x〉，(a，b)a+bx，则容易证明g为环同构，故由推论1知R为交换环.

利用幂零元的性质以及约化理想的结构，可以得到NC环与约化环之间的联系.

命题5设R为半素环，若V2(R)为NC环，则R为约化环.

证若N(R)≠{0}，则有0≠a∈N(R)，从而存在正整数n，使得an-1≠0而an=0，易见n≥2. 由命题4知R为交换环，故

an-1Ran-1=Ran-1an-1=Ranan-2={0}.

由于R为半素环，则an-1=0，矛盾.故N(R)={0}，所以R为约化环.

命题6设I是R的诣零理想.若R为NC环，则商环R/I也为NC环.

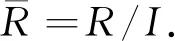
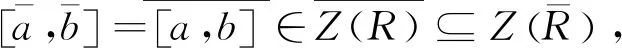
因此商环R/I也是NC环.

命题7设I为R的约化理想，若R/I为NC环，则R为NC环.

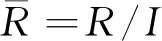
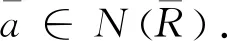
(an-1ta)2=an-1tanta=0.

由于t∈I，则an-1ta∈I，故

an-1ta∈N(R)∩I={0}.

于是an-1ta=0.因为(an-1t)2=an-1taan-2t=0，且an-1t∈I，所以an-1t=0.若n=2，则at=0；若n>2，则(an-2ta)2=0，且an-2ta∈I，故又有an-2ta=0，进一步用上述方法可证，an-2t=0.若n=3，则at=0；若n>3，则重复上述过程，至多有限步，总可得at=0.从而，对任意y∈R，有aty=0.由于(ta)2=tata=0，且ta∈I，故ta∈N(R)∩I={0}，即ta= 0，因此(ayt)2=aytayt=0.由于ayt∈I，则对任意y∈R，ayt=0.由于

t2=[(ab-ba)x-x(ab-ba)]t=a(bx)t-baxt-xabt+xbat=0，

因此t=0，从而对任意x∈R，(ab-ba)x=x(ab-ba).故[a，b]∈Z(R)，所以R为NC环.

命题8设R为有单位元的结合环，则下列条件等价：

(i)R为换位子交换环；

(ii)V2(R)是换位子交换环；

(iii)V2(R)是NC环.

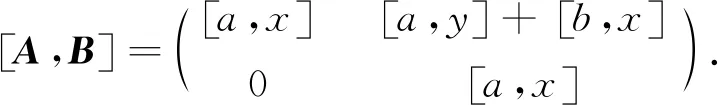
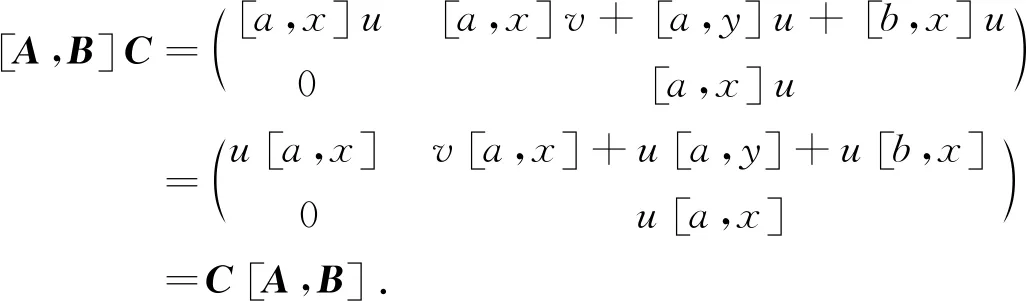
因此[A，B]∈Z(V2(R))，即V2(R)是换位子交换环.

(ii)⟹(iii) 显然.

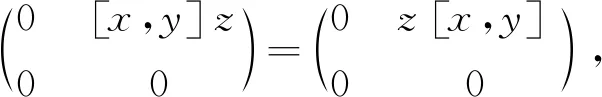
从而[x，y]z=z[x，y]，所以[x，y]∈Z(R).因此R为换位子交换环.

命题9设a是R的正则元，若R为NC环，则a是R的强正则元.

证由于a是R的正则元， 所以存在b∈R， 使得a=aba.记e=ab，g=ba，则

ea=a=ag，e2=e，g2=g.

由于R为NC环，则由命题1知R为Abel环，所以e，g∈Z(R)，于是

a2b=ae=ea=a=ag=ga=ga=ba2，

因此a是R的强正则元.

命题10设R为NC环，若a∈R+，则a∈REP.

证由于a∈R+，所以a=aa+a.由于R为NC环，由命题9的证明知a2a+=a=a+a2，从而

aa+=(a+a2)a+=a+(a2a+)=a+a.

由于a=aa+a，a+=a+aa+，所以a∈R#且a#=a+，从而a∈REP.

命题11设a∈R#∩R+，若[a#，a+]∈Z(R)，则a∈REP.

证由于[a#，a+]∈Z(R)，故[a#，a+]a=a[a#，a+]，即a#a+a-a+a#a=aa#a+-aa+a#.上式左乘a得

aa#a+a-aa+a#a=a2a#a+-a2a+a#

①

由于

aa#a+a=a#aa+a=a#a，aa+a#a=aa+aa#=aa#=a#a，a2a#a+=a(aa#)a+=a(a#a)a+=aa+，

从而①式变为aa+-a2a+a#=0，即aa+=a2a+a#.由于

a2a+a#=a2a+(a#aa#)=a2a+(aa#a#)=a(aa+a)a#a#=aaa#a#=aa#aa#=aa#，

所以aa+=aa#，故a∈REP.

3 结 论

本文主要研究了诣零换位子中心环的一些性质，刻画了这类环的结构.分析了有单位元的结合环R与其上二阶或三阶矩阵环之间的关系，由此得到二阶或三阶矩阵环为诣零换位子中心环的条件.给出了其在局部交换性下呈现的性质，以及其与约化环、Abel环等一些重要环类的联系.除此之外，本文还介绍了诣零换位子中心环上的正则元、强正则元的定义与一些性质，并讨论了其上的广义逆问题，为诣零换位子中心环的应用提供理论基础.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.