一组凹凸性不等式及其应用
赵添润, 王东红, 王岩青
(1.南京航空航天大学 >经济与管理学院,南京211106; 2.南京航空航天大学 >理学院,南京211106;3.中国人民解放军陆军工程大学 >基础部,南京210007)
1 引 言
函数凹凸性是高等数学中函数的一个重要性质. 近年来,国内外许多数学爱好者就函数凹凸性定义之间的联系和性质进行了深入的研究[1-3]. 曲线的凹凸性较广泛地应用于不等式的证明[4]. 本文在原有函数凹凸性定义和性质的基础上,推导出一组新的满足函数凹凸性的不等式,进一步推广到n项形式,并将其应用于求和式数列的极限.
2 函数凹凸性的定义与性质
定义[5]设函数f(x)在区间I上连续,如果对I上任意两点x1,x2(x1≠x2)恒有
f(λx1+(1-λ)x2)>(<)λf(x1)+(1-λ)f(x2) (0<λ<1) ,
则称函数f(x)在区间I上的图形是凸(凹)的.
性质[3]若函数f(x)在区间I上的图形是凸(凹)的, 则对于I内任意三点x1 (1) 定理1设函数f(x)在区间I上有定义,a (2) 即 又因为x>0,所以 f(a)+f(b)≤f(a+x)+f(b-x). (3) 同时,由不等式(1)还可得 (4) 即 又因为x<(b-a),所以 f(a)+f(b)≤f(a+x)+f(b-x) . (5) 同时,由不等式(1)还可得 (6) (7) 由不等式(3)-(7)可知,对∀x∈(0,b-a)不等式(2)成立. 同理,可得如下定理. 定理2设函数f(x)在区间I上有定义,a (8) 不等式(2)的几何解释如下:设函数f(x)在区间I上的图形是凸的,A和B为y=f(x)上的两个点,对∀x∈(0,b-a),当A点的横坐标增加x,B点的横坐标减少x时,得到曲线上相应的两点D和E,则AB的中点C始终位于DE的中点F的下方,如此,直到点D和E的重合为点G(图1).同理,不等式(8)的几何解释如图2所示. 图1 凸函数 图2 凹函数 a+(n-2)Δx=b-Δx;a+(n-3)Δx=b-2Δx;…;a+(n-i)Δx=b-(i-1)Δx. 由定理1可得 即 将上式在i∈[1,n](i为正整数)上累加得 即 同理,可得如下的定理. 本文根据函数的凹凸性给出了两个不等式,并进行了推广,进一步给出不等式在求极限中的应用,例子表明,恰当的运用文中的不等式具有积极的作用. 致谢对相关参考文献给予的启示及审稿人中肯的建议表示感谢!3 一组新的满足函数凹凸性的不等式
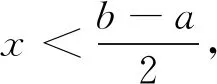
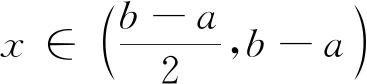
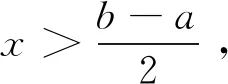
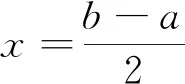

4 定理1和定理2的n项推广形式
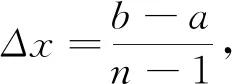

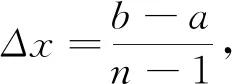
5 应用举例

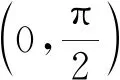
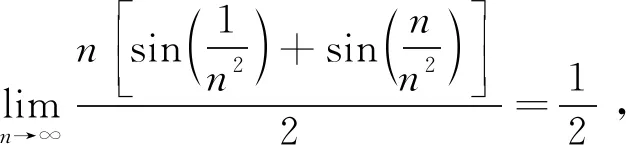

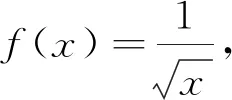
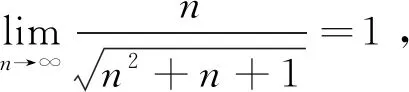
6 结 论

