单纯形法检验数的新计算方法

韩伟一

(哈尔滨工业大学 >经济与管理学院，哈尔滨150001)

1 引 言

自1947年由Dantzig提出著名的单纯形法以来，线性规划的理论和应用研究蓬勃发展，已经成为一门具有丰富内容的成熟学科.当前，求解线性规划的方法主要分为三大类，分别是单纯形方法[1-2]、椭球算法[3]和内点算法[4-5].1972年Klee和Minty给出一个例子表明单纯形方法具有指数时间复杂性，不是一个多项式算法[6].椭球算法尽管是多项式算法，但其实际效果不佳.当前最为推崇的是内点算法，其不仅是多项式算法，而且在实践中具有优良的计算性能，一度认为在大规模稀疏线性规划问题上超越了单纯形法.

尽管单纯形法不是多项式算法，但它具有良好的平均计算性能[7-8].特别是1973年Harris提出最陡边规则[9-10]以后，使得单纯形法与内点法呈现了伯仲难分的态势[1].目前，单纯形法拥有多个变种，大致可分为原始单纯形方法、对偶单纯形方法和原始-对偶单纯形方法等三类.

最早的原始单纯形方法由Dantzig给出，它根据目标函数的最大化或最小化要求，采用最大检验数规则或最小检验数规则确定入基变量，根据广泛流行的θ规则来确定出基变量，根本目的是确定用以矩阵变换的主元.在文献[1]中介绍了几种确定主元的规则，最为常见的有最小或最大检验数规则、最大改进规则[11]和最陡边规则等.无疑，不同的主元规则将产生不同的计算效率，直接决定了单纯形法迭代的次数.值得指出的是，为了避免退化问题对单纯形法造成的影响，潘平奇提出了亏基单纯形方法[12].

检验数在单纯形法中扮演着十分重要的角色，它的一项重要功能是判定当前解是否最优.本文通过给出检验数新计算方法，为有着70多年历史的单纯形法提出一种全新的实施方式.这种计算方式非常简单，可实质性地改变单纯形法的计算步骤，提高单纯形法的计算效率，这将为单纯形方法的教学带来很大的方便[13].

2 检验数计算的新原理

首先给出线性规划的标准形式及其相关定义.定义价值系数向量为C=(c1，c2，…，cn)，资源系数向量为b=(b1，b2，…，bn)T，决策变量向量为X=(x1，x2，…，xn)T，技术矩阵为A，它由n个列向量组成，定义如下

A=[aij]m×n=(p1，p2，…，pn)，

则线性规划的标准形式为

为了行文方便，针对单纯形方法，记

(i)X(B)为基B对应的基可行解，其中非基变量的值为0；

(ii)σ(B)=C-CBB-1A为基可行解X(B)的检验数向量，其中CB=(cB1，cB2，…，cBm)为基变量的价值向量，其中CBi为第i行基变量对应的价值系数；

(iii) 设单纯形法共需要p次迭代，第k(0≤k≤p-1)次迭代过程中相应的基为Bk，总有B0=Im×m；

(iv) 第k次迭代过程中相应的检验数向量为σk(Bk)=(σk1，σk2，…，σkn)，简写为σk.

改进单纯形法及其检验数计算方式的思路是，在保持约束条件不变的情况下，通过改变模型的价值系数形成新的线性规划模型，这个新模型和模型1具有同样的最优解和检验数，且新模型使得检验数的计算更加高效.

设D是模型1的任一可行基，检验数向量σ1(D)=C-CDD-1A为模型1中基可行解X(D)的检验数，令E=σ1(D)，则新模型如下

定理1对于任意一个基可行解，模型1和模型2具有同样的检验数.

证设该基可行解对应的可行基为B，那么模型1的检验数为σ1(B)=C-CBB-1A.

显然B也是模型2的可行基，设模型2中基变量的价值向量为EB，则

EB=CB-CDD-1B.

定义σ2(B)为模型2的检验数，则有

σ2(B)=E-EBB-1A=(C-CDD-1A)-(CB-CDD-1B)B-1A=C-CBB-1A.

从而σ1(B)=σ2(B)，命题成立.

定理2对于某个基可行解，如果其是模型1的最优解，则其也是模型2的最优解.

证若基可行解X1(B1)是模型1的最优基可行解，设最优基为B1，则检验数σ1(B1)≤0.显然X1(B1)是模型2的基可行解，相应的可行基也为B1.

根据定理1，既然σ1(B1)=σ2(B1)，从而有σ2(B1)≤0，故X1(B1)也是模型2的最优基可行解.

定理1和定理2表明，可以用模型2来获得模型1的最优解.

定理3若X是模型1和模型2的基可行解，D是相应的可行基，设模型1的目标函数值为z1，模型2的目标函数值为z2，则z1=z2+CDD-1b.

证由于z2=(C-CDD-1A)X=CX-CDD-1AX.又因为AX=b且z1=CX，从而

z1=z2+CDD-1b.

推论1模型1和模型2等价.

证两个模型具有同样的约束条件，且目标函数值相差一个常数，因而两模型等价.

3 原始单纯形法的新计算方式

利用上述结论可以改变原始单纯形法的计算方式.原始单纯形法的计算步骤如下：

步骤1 给出初始的基可行解，并使得相应的基为单位阵.

步骤2 计算检验数，根据检验数判定最优解的状况.在发生无解或无界的情形下，算法结束，否则转入步骤3.

步骤3 根据入基规则(本文采用最大检验数规则)，确定入基变量；根据θ规则确定出基变量；根据入基变量和出基变量的下标确定主元.

步骤4 以主元为中心进行矩阵变换得到新的基可行解.再转到步骤2.

在上述原始单纯形法中，采用的入基规则可以为最大检验数规则、目标函数值最大改进规则或其它规则.新的计算方式如下

步骤1 给出初始的基可行解，并使得相应的基为单位阵，k=0，基为Bk=Im×m.

步骤2 计算检验数向量σk，根据检验数判定最优解的状况.在发生无解或无界的情形下，算法结束，否则转入步骤3.

步骤3 根据入基规则(本文采用最大检验数规则)，确定入基变量；根据θ规则确定出基变量；根据入基变量和出基变量的下标确定主元.

步骤4 以主元为中心进行矩阵变换得到新的基可行解.

步骤5 把模型的价值向量改变为σk.k=k+1转入步骤2.

下面以例1来说明新计算方式的计算效率

例1maxz=4x1+6x2+x3+x4-x5-2x6.

采用单纯形表，计算过程如下

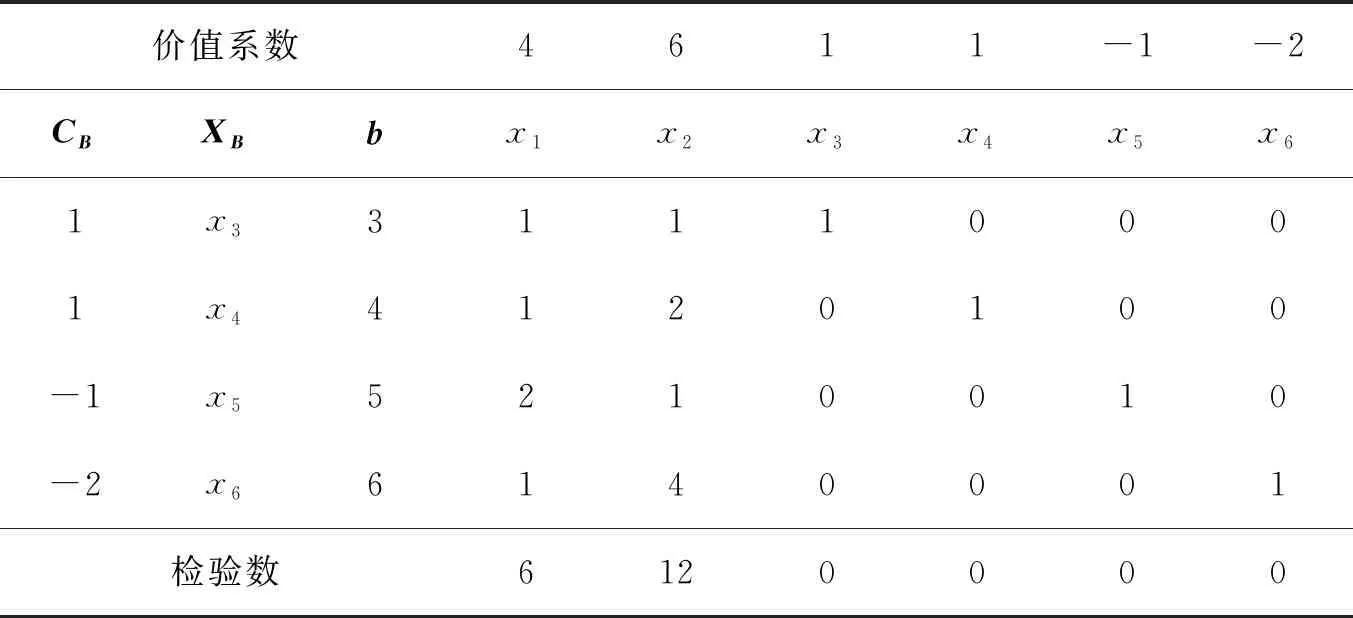
表1 第一个单纯形表

表2 第二个单纯形表

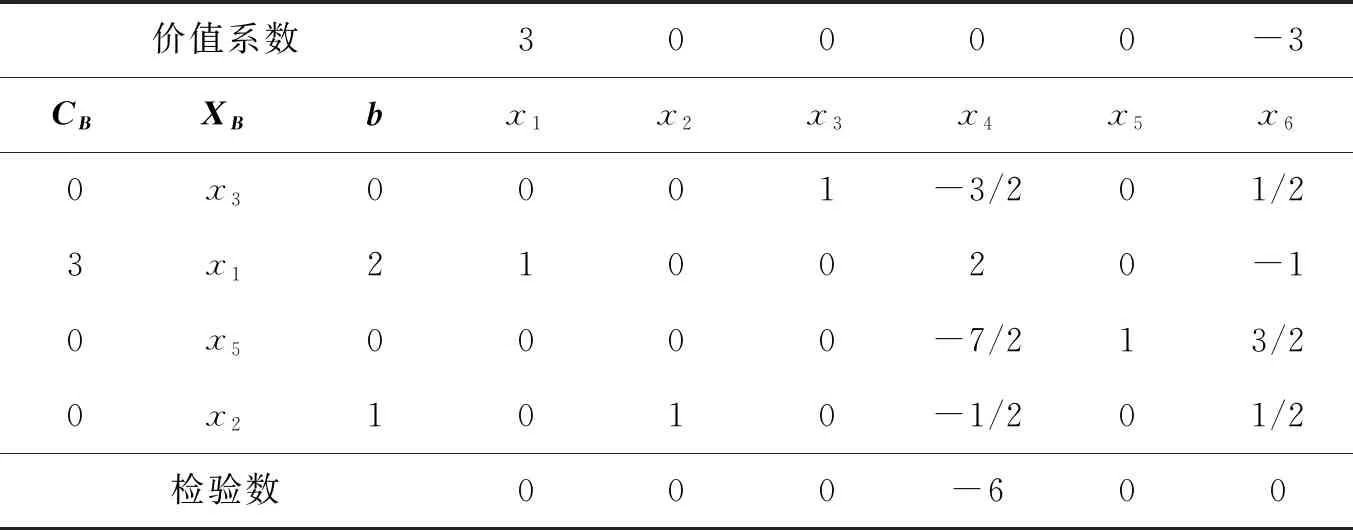
表3 第三个单纯形表

根据上例可以看出，新计算方法之所以能提高计算效率，根本原因在于：用检验数替换价值系数后，基变量的价值系数向量总有m-1个分量为0，这给检验数的计算带来了极大便利，因而能够显著提高检验数的计算效率.

根据新计算方式，还可得到如下重要的结论

性质1对于新计算方式，从第2个表开始，基变量的价值系数总是非负的.

证根据前述基变量的价值系数有m-1个的值为0，另外一个为上个表中入基变量的检验数，因而只能为非负.命题得证.

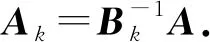
性质2根据新计算方式，可得检验数的递推公式如下

证根据检验数计算公式及新计算方式的过程立即可得.

4 修正单纯形法的新计算方式

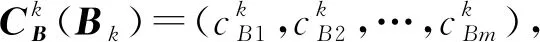
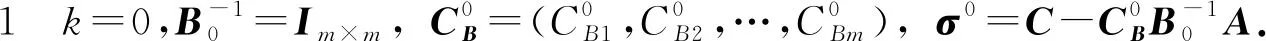
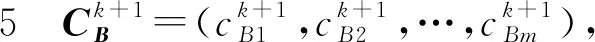
步骤7k=k+1， 重复步骤2.

下面用例1来对比原修正单纯法和新方法的区别.原方法的计算步骤如下：

当k=0时：

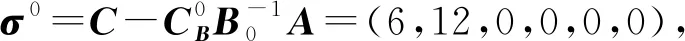
3:选取最大检验数对应的变量x2为入基变量，

当k=1时：

7:选取最大检验数对应的变量x1为入基变量，

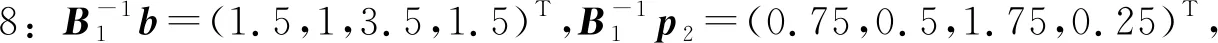
当k=2时：

由于所有检验数非正则求解过程结束.

相对于原方法，新方法仅需修改如下两个步骤：

5 结 论

本文使用检验数来替换价值系数得到了线性规划模型的等价模型，进而给出了单纯形法的新实现方式.这种新方式显著提高了单纯形法检验数的计算效率，提升了单纯形法的计算绩效，实质性地改变了单纯形法的计算步骤.这种新方式尽管原理简单，但它具有很广的应用价值，还可以应用于对偶单纯形法、目标规划单纯形法、运输单纯形法等多个场合，能够提高这些方法的计算效率，无疑将有利于运筹学的教学.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.