如何不用复数讲解常系数线性微分方程

严质彬， 包益欣

(哈尔滨工业大学(深圳) >理学院， 广东 >深圳518055)

1 引 言

关于常系数线性微分方程的教学， 文献中有很多有趣的研究[1-5]. 本文讨论高等数学课程的教学实践中， 关于常系数线性微分方程的一个与复数有关的问题.

考虑二阶常系数齐次线性微分方程

y″+py′+qy=0.

(1)

这里y=y(x)是待求的未知函数(x是实的自变量)，p和q是已知实数. 关于未知数r的实系数二次代数方程

r2+pr+q=0

(2)

称为(1)的特征方程. 为了得到(1)的解， 通常用含有待定未知数r的指数函数y=erx来试解. 由于对一般的系数p和q， 特征方程(2)可能无实数根， 为了得到完整的理论， 要允许r是复数. 当r=a+bi为复数时(b≠0)， 关于实自变量x的复值函数y=e(a+bi)x的定义， 导数公式(erx)′=rerx，复指数的性质ez1+z2=ez1ez2(z1，z2为复数)及欧拉公式

e(a+bi)x=eax(cosbx+isinbx)

的确切含义及证明， 要等到后面讲函数项级数(幂级数的乘法、逐项求导等)时才能学到. 目前的教学实践中， 留给函数项级数的教学课时往往不多， 复指数函数的知识经常不讲解或者一带而过. 所以说高等数学课程中， 常系数线性微分方程的教学在逻辑上有些不足. 本文探讨不用复数， 且用比复指数讲解更少的课时， 如何自然地讲解常系数线性微分方程.

2 复值函数解导出实值函数解的分析

在现有高等数学课程的教学中， 用复指数函数来讲解常系数线性微分方程， 其不足之处并不仅限于要用到后面很晚才学到的知识. 还有另外一点微妙的困难.

设a±bi(b≠0)是(2)的一对共轭复数根， 于是

y1=e(a+bi)x=eax(cosbx+isinbx)，y2=e(a-bi)x=eax(cosbx-isinbx)

是(1)的两个(线性无关的)解. 这里的微妙之处在于：它们是实自变量x的复值(复因变量)函数解. 学习者在自觉不自觉中， 自然是期待实值函数解. 方程的物理意义(电感电容电阻电路， 或者弹簧质量阻尼振动)也是要求实值函数解. 教学中都是通过y1和y2的复系数线性组合

(3)

(4)

根据叠加原理[6]来得到实值函数解. 整个过程形象地说， 是从实数领地的问题出发， 漫游到复数的王国， 最后又回到实数的领地. 在教学实践中， 学生对这个过程经常感到莫名其妙. 对于这种推导， 除了指出叠加原理的作用外， 认为还有其他值得讲解的重要细节.

问题本身是要在实自变量的实值函数的范围内寻找(1)的解， 这样的解的集合是实数域上的线性空间. 先在实自变量的复值函数的范围内寻找(1)的解，这样的解的集合是复数域上线性空间. 把实值函数看作复值函数的特例， 则上述前一个集合是后一个集合的严格子集合. 但前者作为实数域上的线性空间和后者作为复数域上的线性空间有相同的维数， 都是2， 这和它们之间有严格子集关系并不矛盾. 复值函数e(a+bi)x和e(a-bi)x是复值函数解集合作为复线性空间的基底(基础解系)， 它们不是实值函数解. 但这不妨碍它们的复值线性组合(当然是解)有可能组合出实值函数解来: (3)和(4)就是这样的特殊复值线性组合.

先在扩大的范围内寻找“广义解”， 再研究如何从“广义解”返回“狭义解”. 这种思想的重要性在数学及其应用中十分重要， 只要有机会就应该尽可能传授给学生. 这并不是什么现代数学的深奥思想， 在中学数学中就有这种思想的种子: 例如整系数多项式分解因式， 可以在复系数多项式范围内分解， 可以在实系数范围内分解， 可以在有理系数范围内分解， 可以在整系数范围内分解. 先在大的范围内求解， 再根据问题的需要， 回到小范围， 是中学生就懂得的道理.

3 不用复数推导出实值函数解的方法

这里给出不用复指数函数， 甚至完全不用复数的推导方法.

首先， 引导学生观察下面的事实: 对任意给定的实数c和d， 实自变量x的实值函数

ecxcosdx， ecxsindx

的各阶导数都是它们自己的线性组合. 为方便陈述， 把这个事实写成引理的形式.

引理1ecxcosdx及ecxsindx的一阶和二阶导数为

(ecxcosdx)′=cecxcosdx-decxsindx，(ecxsindx)′=decxcosdx+cecxsindx，(ecxcosdx)″=(c2-d2)ecxcosdx-2cdecxsindx，(ecxsindx)″=2cdecxcosdx+(c2-d2)ecxsindx.

根据上述观察， 可以用含有两个待定的未知实数a和b的实自变量x的实值函数

y1=eaxcosbx，y2=eaxsinbx

来试解(1).由引理1， 经简单计算， 有

y″1+py′1+qy1=(a2+pa+q-b2)eaxcosbx-(2a+p)beaxsinbx，

(5)

y″2+py′2+qy2=(2a+p)beaxcosbx+(a2+pa+q-b2)eaxsinbx.

(6)

容易得到下面的定理.

定理1设a和b是实数. 则实自变量x的实值函数y1=eaxcosbx是二阶常系数齐次线性微分方程(1)的解的充要条件是a和b满足

(7)

证充分性由(5)显然. 下证必要性. 由y1=eaxcosbx是解及(5)有

(a2+pa+q-b2)eaxcosbx-(2a+p)beaxsinbx=0.

注意这是关于自变量x的函数等式， 也就是代入自变量x的任意值， 等式都成立. 以x=0代入并注意到对任意x，eax>0， 即得

a2+pa+q-b2=0.

于是得函数等式

(2a+p)beaxsinbx=0.

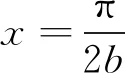
定理2设a和b是实数. 则实自变量x的实值函数y2=eaxsinbx是二阶常系数齐次线性微分方程(1)的非零解的充要条件是a和b满足(7)且b≠0.

证充分性显然. 下证必要性. 由y2=eaxsinbx是解及(6)有函数等式

(2a+p)beaxcosbx+(a2+pa+q-b2)eaxsinbx=0.

以x=0代入， 即得(2a+p)b=0及函数等式

(a2+pa+q-b2)eaxsinbx=0.

(10)

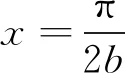
a2+pa+q-b2=0.

注意在定理2的陈述中有一个微妙的条件“非零解”， 而在定理1中没有加这个条件. 对y2=eaxsinbx来说， 当b=0时， 对任意的a，y2都是解(零解)， 但不是对任意的a， 方程组(7)都满足.

有人可能会觉得， 一开始就用带有两个待定未知实数a和b的函数eaxcosbx及eaxsinbx去试解微分方程(1)“不自然”. 其实， 这种试解方法无非就是受到下述事实的启发: 所试用的函数类对于求导具有某种封闭性. 在教学实践中， 注意启发学生观察引理1所蕴含的这种“封闭性”. 有了这个铺垫， 则用eaxcosbx及eaxsinbx去试解， 不会比用erx去试解更“不自然”， 何况后者还要用到没有学过的、其证明并非一蹴而就的复指数函数的知识. 反过来说， 如果对上面的“封闭性”不作启发和强调， 则学生也会对用erx去试解感到“不自然”. 所以在这个问题上， 学生是否感到“自然”而不是觉得被牵着鼻子走， 并不取决于用了含多少个待定参数的函数来试解， 而是取决于对上面的“封闭性”是否作了启发式的讲解.

以a，b作为未知数， 求方程组(7)的实数解非常简单， 其讨论不会增加课时. 为方便起见，总结成下面的定理.

定理3设p和q是给定的实数. 则以a和b为未知数的方程组(7)恒有实数解. 且有

(i) 若p2-4q≥0， 则(7)的实数解是

(ii) 若p2-4q<0， 则(7)的实数解是

4 与复数方法的关系

定理4设p和q是给定的实数. 则(a，b)是方程组(7)的实数解的充要条件是r=a+bi是特征方程(2)的复数解.

证将r=a+bi代入(2)经简单计算， 比较复数等式两边的实部和虚部， 即得方程组(7).

容易看出， 上述第3节的讨论完全不必以定理4为前提.

5 结 论

不用复指数函数， 甚至不用复数， 可以讲解常系数线性微分方程的解的理论.

致谢感谢审稿人对本文的仔细阅读和提出的修改意见.