n维模糊数值函数Henstock-Stieltjes积分原函数的可导性与导函数的可积性

肖志勇， 王欣欣

（陇东学院数学与统计学院，甘肃庆阳745000）

为了处理一些不确定、模糊问题，模糊数学得以发展，其中，模糊分析学中的模糊数值函数微积分理论是一个重要的研究方向［1-4］.在实值函数情形下，Stieltjes积分可以看作是Riemann积分的推广.对于模糊数值函数，Nanda［5］和 Wu［6］从不同角度定义了Riemann-Stieltjes积分.文献［7-8］发现了连续的模糊数值函数关于单调不减函数是Riemann-Stieltjes可积的.2010 年，巩增泰等［9］定义和讨论了一维模糊数值函数的Henstock-Stieltjes积分及其性质，研究了积分原函数的可导性与导函数的可积性.2014年，刘坤等［10］定义了n维模糊数值函数的Henstock-Stieltjes积分，并给出了一些性质.2017年，崔建斌等［11］讨论了n维模糊数值函数的Henstock-Stieltjes积分的性质，并利用集值函数、向量值函数以及实值函数的Henstock-Stieltjes积分给出了其刻画定理.本文利用支撑函数讨论了n维模糊数值函数Henstock-Stieltjes积分原函数的可导性与导函数的可积性.

1 预备知识

本文中用En表示n维模糊数空间.模糊数∈En，是指是正规、凸模糊集，隶属函数 u（x）是上半连续函数且具有紧支集［1］.对在模糊数空间En中加法及数乘运算分别定义为：

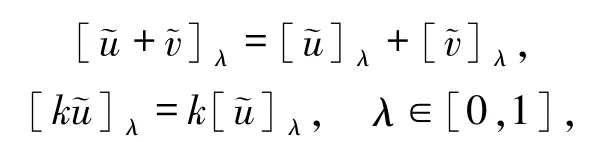
其中，当 λ∈（0，1］时，有

当λ＝0时，有

定义

引理 1.1［1］设∈En，则：

2）若0≤λ1≤λ2≤1，有

3）若正数列｛rm｝非降收敛于 r∈（0，1］，有

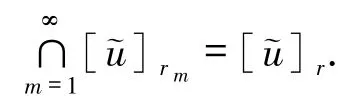
反之，若对任何 r∈［0，1］，均存在 Ar⊆Rn满足上述条件1）～3），则存在唯一的模糊数，使得对且

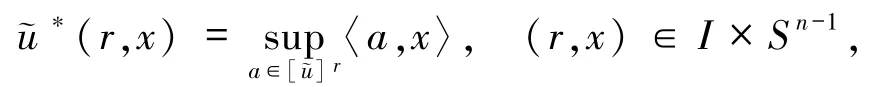
其中，I＝［0，1］，Sn-1是 Rn的单位球面，即

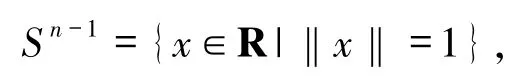
〈·，·〉是Rn中的内积.

引理 1.2［12］若1］，那么

2）当 k≥0 时，u*（r，kx）＝ku*（r，x）；

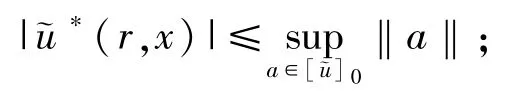
2 主要结果

定义2.1设n维模糊数值函数关于实值增函数 α（t）在 t0∈［a，b］处 α - 可导，是指En，使得极限

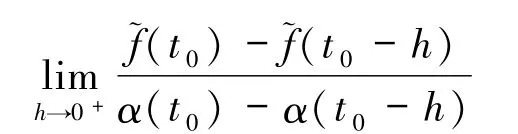
定义2.2设n维模糊数值函数关于实值增函数 α（t）在 t0∈［a，b］处 α -支撑可导，是指使得极限

和

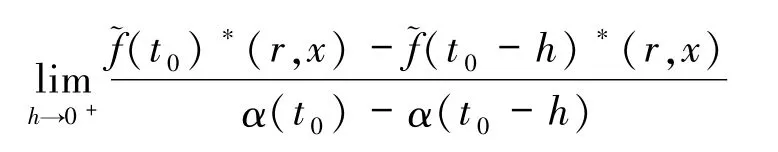
对（r，x）∈I× Sn-1一致存在且等于称之为在 t0处的 α - 支撑导数，记为，即

定理 2.3设 n 维模糊数值函数上满足 H-差性质，则处 α - 可导的充分必要条件是处 α - 支撑可导，且

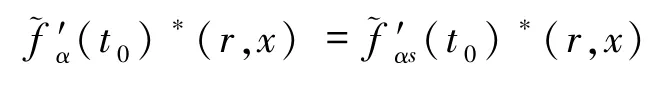
或

证明必要性 因为在 t0∈［a，b］处 α -可导，则存在n维模糊数使得

即∀∈＞0，∃δ＞0，当0＜h＜δ时，有

所以，极限

对（r，x）∈I× Sn-1一致存在且等于.同理，可证对任意x∈Sn-1，极限

对（r，x）∈I× Sn-1一致存在且等于即在 t0∈［a，b］处 α -支撑可导，且

和

或

即∀∈＞0，∃δ＞0，当 0＜h＜δ时，对（r，x）∈I×Sn-1一致有

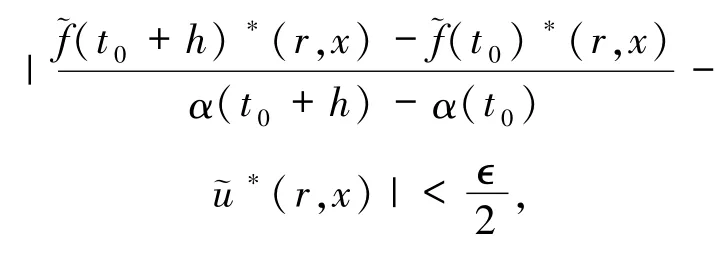
所以∀∈＞0，∃δ＞0，当0＜h＜δ时，有

即

即

定义 2.4［10］n 维模糊数值函数关于实值函数 α（t）在［a，b］上模糊 Henstock-Stieltjes可积，是指存在，对任意给定的∈＞0，存在定义于［a，b］上的正值函数 δ（t），使得对［a，b］上的任何δ-精细分法 T＝｛［u，v］，ξ｝，有

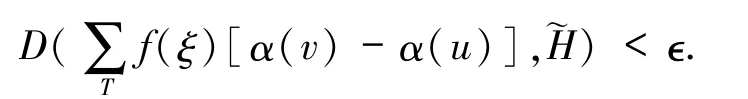
定理 2.5设是［a，b］上的 n 维模糊数值函数，α（t）为实值增函数，则的充分必要条件是对任意的 x∈Sn-1，实值函数在［a，b］上关于 α 对 r一致（HS）可积（δ（t）的选取与 r无关），且

证明必要性 若

则对任意 ∈＞0，存在定义与［a，b］上的正值函数δ（t），使得对［a，b］上的任何 δ- 精细分法 T＝｛［ti-1，ti］；ξi｝有

因此

所以，对任意的 x∈Sn-1，有

充分性的证明类似于文献［8］定理2（5）→（1）.

定理 2.6设 n 维模糊数值函数是［a，b］上连续，α（t）为实值增函数，则在［a，b］上α -可导，且对任意的 t∈［a，b］，有

其中

证明显然，对任意的H-差存在.因为 n维模糊数值函数上连续，因此对任意 ∈＞0，存在 δ＞0，当0＜h＜δ时，有所以，对任意 ∈＞0，存在 δ＞0，当0＜h＜δ时，对（r，x）∈I×Sn-1一致有

即

对（r，x）∈I× Sn-1一致存在且等于.类似地，有

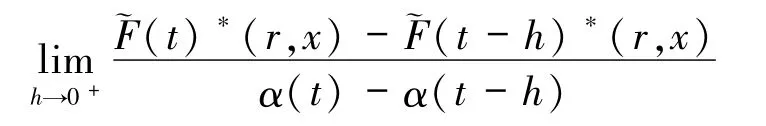
对（r，x）∈I× Sn-1一致存在且等于因而在 t处的 α -支撑可导.所以，根据定理2.3，在 t处的 α -可导，且

定理 2.7设n 维模糊数值函数是［a，b］上满足H-差且α-可导，则

且

证明因为n维模糊数值函数是［a，b］上满足H-差且α-可导，所以根据定理2.3可知，对任意 ∈＞0，存在 δ＞0，当

时，对r一致有

由上面两式得

从而，对任意的 ∈＞0，存在 δ（t）＝δ，使得对［a，b］上任意δ-精细分法

有

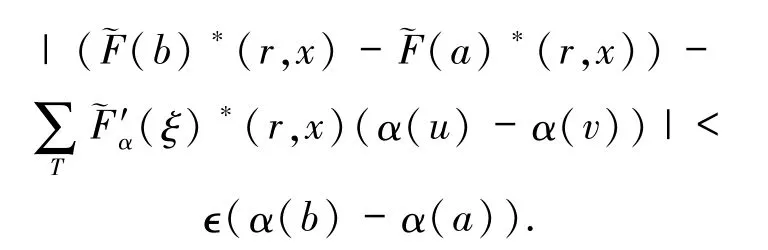
所以对任意的 x∈Sn-1，实值函数在［a，b］上关于 α 对 r一致（HS）可积，且

即

根据定理2.5有

且

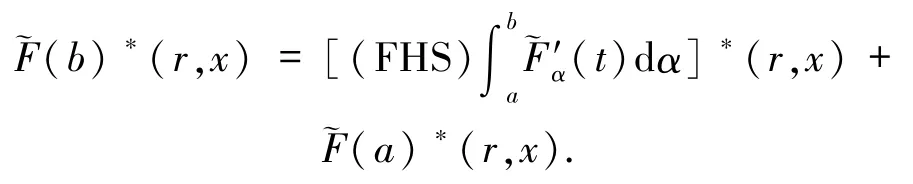
因而

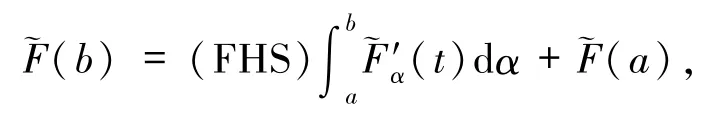
即