具有随机干扰和无症状感染者的疟疾模型研究

王生福， 聂麟飞

（新疆大学数学与系统科学学院，新疆乌鲁木齐830046）

疟疾是世界上最具破坏性的疾病之一.尽管随着医疗科技的飞速发展，近年来死亡人数下降了30%，但每年仍有数百万人死亡［1］，其中受影响最严重的是儿童.据医疗数据统计发现，在疟疾的流行区域，大约50%的疟疾感染者是无症状的［2-3］.由于无症状患者不太可能寻求治疗，因此这些人有可能将疾病传播给其他人，使得疟疾在某些地区长期流行.基于上述原因，众多国内外学者建立了大量的动力学模型去了解疟疾的传播规律和措施［4-8］.特别地，Tang 等［7］提出了如下具有无症状感染和季节影响的SIRS疟疾传播模型：

其中 S（t）、Ia（t）、Is（t）、R（t）分别表示 t时刻人群中的易感者、无症状染病者、有症状染病者和恢复者的数量.模型假设易感者每次接触被传染的概率为β，μ是人的自然死亡率；无症状染病者的数量占总染病者的数量的比率为θ，有症状染病者和无症状染病者的恢复率系数分别为γs和γa，有症状染病者和无症状染病者康复后失去免疫率的系数为α；因有症状的感染者将在医院接受治疗或隔离，所以易感者接触有症状感染者时被传染的概率为βp，其中 p∈［0，1］.

由模型（1）不难发现人口总数N（t）为常数，即N（t）＝N.进一步，忽略季节对疾病的影响，则模型（1）等价于下面的简化模型

由文献［7］可知，模型（2）的基本再生数

即当R0＜1时，模型（2）仅有一个无病平衡点E0＝（N，0，0），且是全局渐近稳定；而当 R0＞1 时，模型（2）存在地方病平衡点，且是局部渐近稳定，这里由下式决定

事实上，环境白噪声也会对传染病模型造成一定的影响［9-13］.因此，在传染病动力学模型中加入环境白噪声更具有现实意义［10，14-16］，已有许多学者进行了相关研究.例如文献［15］指出，环境白噪声可以改变传染病模型的基本再生数.此外，环境白噪声也可以使模型参数在一定范围内发生改变，如出生率、死亡率以及传播率系数等会受到干扰而围绕某些数值波动.有基于此，假设环境白噪声的影响分别与变量 S（t）、Ia（t）和 Is（t）成正比，则模型（2）可随机化为

这里 Bi（t）（i＝1，2，3）是相互独立的标准布朗运动，（i＝1，2，3）是白噪声强度.

1 非负性与有界性

令（Ω，R，{Rt}t≥0，P）是一个带有滤子的完备概率空间并且满足通常的条件（即滤子R0是单调递增，右连续的，并且包含所有的零测度集）.记＝｛（x1，x2，x3）：xi＞0，i＝1，2，3｝，f（t）是定义在［0，∞）上的可积函数，令

定理1.1对任意给定的初值

模型（3）存在唯一解（S（t），Ia（t），Is（t）），且该解以概率1位于中.即对于所有 t≥0，有（S（t），Ia（t），Is（t））∈，a.s..

证明因模型的参数是局部Lipschitz连续的，故对于任意给定的初值（S（0），Ia（0），Is（0））∈，模型（3）存在唯一的局部解（S（t），Ia（t），Is（t）），t∈［0，τe），这里 τe表示爆破时间.为了证明这个解是全局存在的，只需证明τe＝∞几乎处处成立.设 k0＞1 且足够大，使其满足（S（0），Ia（0），Is（0））∈（1／k0，k0）.对于每个整数 k ＞ k0，定义停时

其中，infØ＝∞（Ø表示空集）.显然，当k→∞时，τk单调递增的.令则 τ∞＜ τe，a.s..若τ∞＝∞，a.s.，则 τe＝∞，a.s..因此，只需证明τ∞＝∞，a.s.即可.

易知 V（S，Ia，Is）非负，对其应用 Itô公式可得

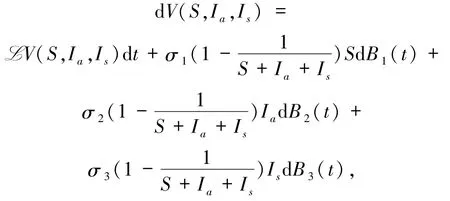
其中

显然K为正常数，且

将（5）式两边从0到τk∧T积分并取期望得

因此，

令 Ωk＝｛τk≤T｝，k≥k1，由（4）式可知，P（Ωk）≥ε.对于每个 ω∈Ωk，由停时的定义可知，在 S（t）（τk，ω），Ia（t）（τk，ω），Is（t）（τk，ω）三者中至少有一个等于 k 或1／k，可得

其中

进一步，由（6）式可知

其中 IΩk（ω）为 Ωk的示性函数.令 k→∞ ，则有

矛盾.所以 τ∞＝∞.这就意味着（S（t），Ia（t），Is（t））以概率1在有限时间内不会产生爆破.证毕.

引理 1.2设（S（t），Ia（t），Is（t））是模型（3）满足初值条（S（0），Ia（0），Is（0））∈的解，则以下结论成立：

且

证明由模型（3）知

令 μ＋α＝μ1，求解（9）式可得

其中

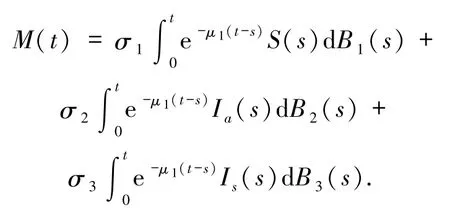
显然，M（t）是一个连续的局部鞅并且满足M（0）＝0.定义

其中

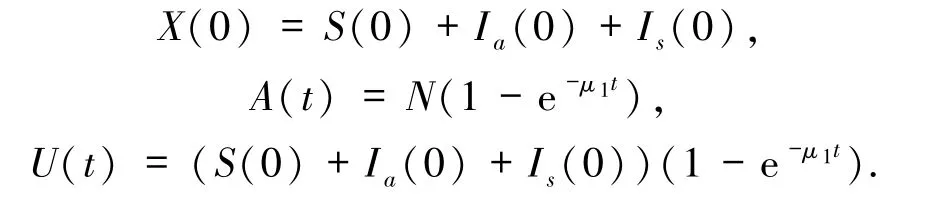
由等式（10）可知

于任意的 t≥0 成立，表明 A（t）、U（t）是 t≥0 上满足A（0）＝U（0）＝0的连续自适应过程.由文献［9］中的定理3.9知.由此，结论（7）成立.令

由二次变分

由强大数定理［10-11］知

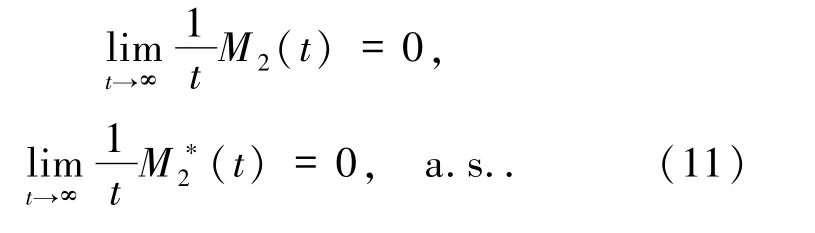
同理，

因为

则由（11）和（12）式可知

由此得出结论（8）是正确的.证毕.

2 持久性和灭绝性

定理 2.1设（S（t），Ia（t），Is（t））是模型（3）满足初值条件（S（0），Ia（0），Is（0））∈的解.如果

则

且

证明由模型（3）可知

对上式关于0到t积分得

于是

其中

易知，

另一方面，对模型（3）的后2个等式使用Itô公式有

对上式从0到t积分得

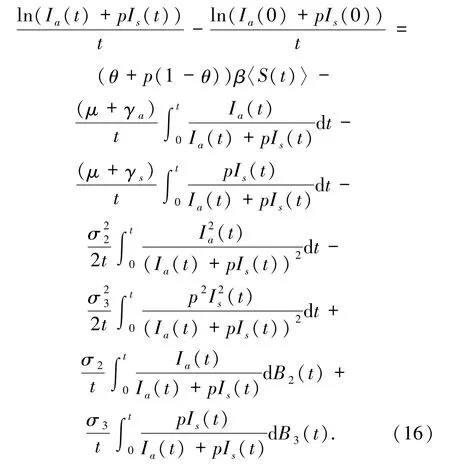
把（14）式代入（16）式可知

又因为

根据（15）和（18）式对等式（17）两边取上极限，并注意到＾R0＜1，则有

即

进一步，由（14）和（15）式可知

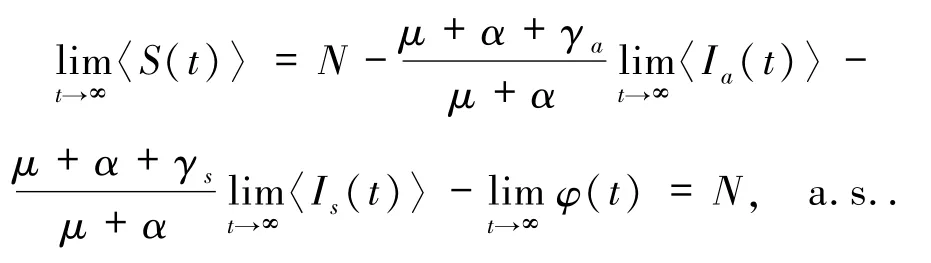
证毕.

定理 2.2若 α＝0，且

则模型（3）是持久的，即

其中（S（t），Ia（t），Is（t））∈R3＋是模型（3）的任意解.

证明由模型（3）的第2个等式可得

进而，

同理，由模型（3）的最后一个等式可得

于是，由（19）和（20）式可知

根据等式（17）可知

根据等式（15）和（21）对上式两边取下极限，并注意到¯R0＞1，则有

max｛（μ＋γa），（μ＋γs）｝（¯R0-1）＞0， a.s..因而，

再由模型（3）知

进而，

故定理成立.证毕.

3 结论

本文研究了一类具有随机干扰和无症状感染者的SIRS疟疾模型，这里假设环境白噪声的影响分别与变量 S（t）、Ia（t）和 Is（t）成正比.首先考虑了模型（3）全局正解的存在性与唯一性、有界性.其次证明了模型（3）的随机持久性和灭绝性.定理2.2指出当¯R0＞1且满足α＝0时，模型（3）是持久的，即疾病持续成“地方病”.然而由定理2.1可知，当＾R0＜1时，疾病依概率1灭绝.

然而，在传染病的传播过程中，传播方式的复杂性、病毒的变异性、种群的异质性、统计数据的不完整性、以及环境因素和人为干扰的不确定性使疾病的预防和控制面临新的形势与挑战，这些都是将要开展的研究工作.