多粒度实值形式概念分析

李金海，邓小媛，智慧来

(1 昆明理工大学 数据科学研究中心，云南 昆明 650500； 2 昆明理工大学 理学院，云南 昆明 650500； 3 河南理工大学 计算机科学与技术学院，河南 焦作 454000)

形式概念分析提出的本意是希望对哲学上的抽象概念进行数学上的形式化描述与研究，最早从事该研究的是德国数学家Wille教授[1]及其团队[2]。国内于2000年左右开始关注概念格与关联规则挖掘等领域的研究[3-5]，主要聚焦国际上比较热门的基本问题提出新的研究方法。此后10年，国内学者开始对概念格约简感兴趣，给出了各种概念格约简方法[6-11]。2011年以来，许多学者围绕决策形式背景上的概念格约简开展研究[12-17]，这些研究主要基于张文修团队提出的决策形式背景[18]。与此同时，一些学者又相继提出了若干新颖的研究课题，比如多粒度形式概念分析[19]、概念认知学习[20-25]、粒描述[26-27]等，这些新兴的研究方向大大促进了经典形式概念分析的发展[28]。

一方面，在研究形式概念分析时，实值是描述形式背景的对象与属性之间关系最为复杂的数据类型之一[29]，它对应的概念格既是区间值概念格的推广[30-31]，又是模糊概念格的扩展[32-34]，这种推广或扩展是针对取值范围的延拓，因其应用广泛而受到众多学者的关注[12,14]。此外，实值概念格的并行构造也得到了重视，这类问题主要侧重快速计算概念节点[35]。另一方面，粒计算与形式概念分析的结合日渐深入，从最早的粒概念及其约简开始[8]，到随后的概念知识粒与概念信息粒[36]，以及近期开展的一系列跨领域、深层次、多角度的融合研究，充分表明这两个理论有非常好的结合性[37-38]。特别地，自从将粒计算中的多粒度思想[39-40]引入形式概念分析后，很快建立了多粒度形式概念分析理论[41-43]，并成为热门研究话题[44-45]。为了进一步拓宽实值概念格的应用范围，还需继续研究多粒度实值形式概念分析，即如何借助多粒度思想探讨实值概念知识发现与规则提取。

鉴于上述分析，本文基于多粒度数据或多粒度关系提出多粒度实值形式概念分析方法，旨在探究多粒度概念知识空间的概念转移规律以及规则推理的运算关系，具体提出了实值类属性块以及多粒度实值形式背景，给出了带决策的多粒度实值形式背景的知识发现方法，为今后多粒度实值数据的多层次知识发现研究奠定了理论基础。

1 实值形式背景与实值概念

(1)

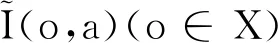
Δ(A)=

是实值属性集A上的所有实集构成的集合，其中μt(ai)(i=1,2,…,m)是实区间集。算子↑:2U→Δ(A)和↓:Δ(A)→2U定义为

(2)

从(2)式可以看出，

(3)

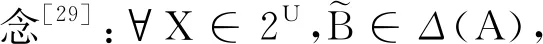
2 多粒度实值形式背景

前文讨论了实值形式背景和实值概念，下面再将多粒度思想引入实值形式背景中，提出多粒度实值形式背景。为此，约定来源于同一类别(类型)的实值属性构成的集合称为实值类属性块。

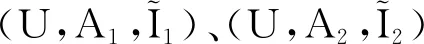
(4)

需要指出的是，本文提到的粒度粗细均包含了粒度相等的情况。

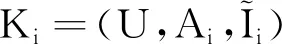
实际上，多粒度实值形式背景刻画了实区间集赋值之间的一种关系。具体地，对于描述一个对象的问题，可以选择在粒度粗的属性下进行统一的笼统描述，也可以选择在粒度细的多个分属性下进行具体的描述。当然，在不同的粒度空间下描述对象，其提供的信息是不等价的，细粒度空间中的描述通常比粗粒度空间中的描述给出了更多可供参考的信息。

(5)

根据假设，{as}s∈S、{bt}t∈T均为布尔属性集，且{as}s∈S和{bt}t∈T拥有的对象形成论域U的划分。那么对于任意对象o∈U，由公式(4)可得fo(ai)=fo(bj1)∪fo(bj2)∪…∪fo(bjk)成立。因此，当fo(ai)=∅时，fo(bjt)(t=1,2,…,k)均为∅；当fo(ai)={1}时，fo(bjt)(t=1,2,…,k)中有一个为

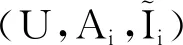
性质1表明多粒度实值形式背景是经典多粒度形式背景的推广。为了叙述方便，本文讨论的多粒度实值形式背景均默认形成特化全序关系，即实值类属性块的粒度越来越细；另外，最粗的实值类属性块的元素个数均设为1，这是出于画粒度树的需要。

由于前面已约定最粗的实值类属性块的元素个数均为1，那么粒度树的根节点通常只有一个。此外，根据定义5，来自同一粒度空间的属性要求排在同一层，那么每棵粒度树的总层数均为r，即与多粒度实值形式背景的粒度层数相同。

表1 实值形式背景

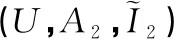
表2 实值形式背景

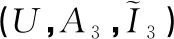
表3 实值形式背景

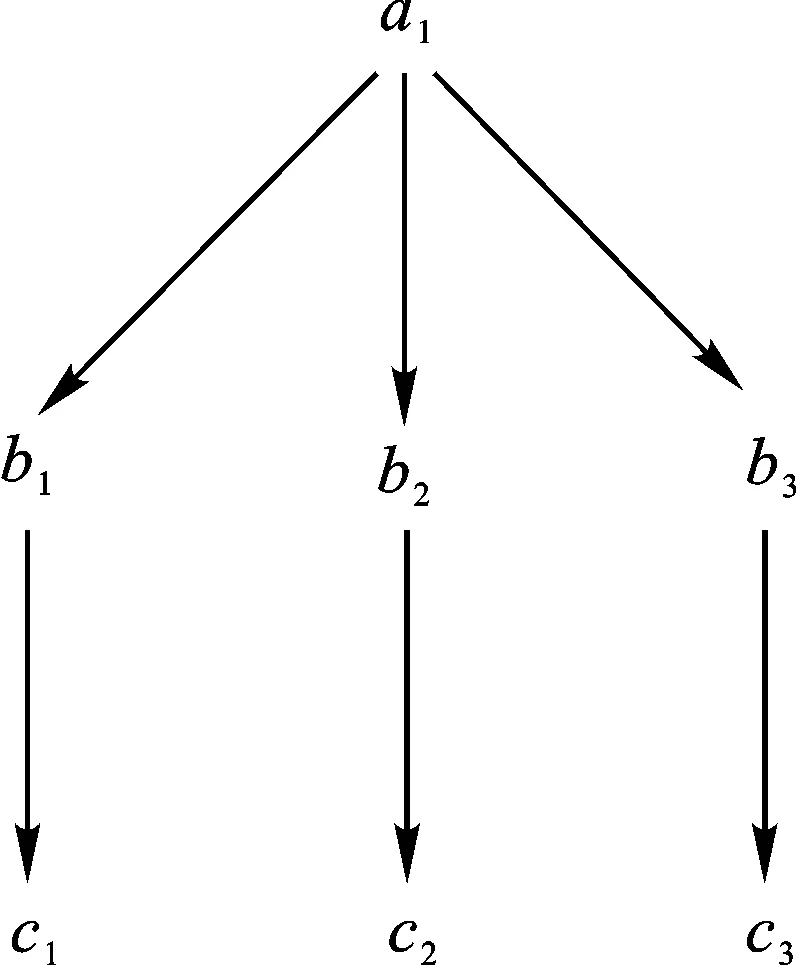
图1 属性a1的粒度树Ta1

图2 属性a2的粒度树Ta2

容易验证，对表1～3的实值形式背景并置形成一个多粒度实值形式背景。具体地，由图1可知表1的类属性块{a1}比表2的类属性块{b1,b2,b3}粒度粗，表2的类属性块{b1,b2,b3}与表3的类属性块{c1,c2,c3}粒度粗细相同；由图2可知表1的类属性块{a2}比表2的类属性块{b4,b5}粒度粗，表2的类属性块{b4,b5}又比表3的类属性块{c4,c5,c6,c7}粒度粗。

证明设粗粒度实值形式背景的L-实概念的外延为X。一方面，在细粒度实值形式背景中X的每个对象仍属于X对应的诱导L-实概念(X↑↓,X↑)；另一方面，对于任意对象o∈U-X，它肯定不属于X对应的诱导L-实概念(X↑↓,X↑)，否则可以推出对象o在粗粒度实值形式背景中也属于外延X，这与X是L-实概念的外延矛盾。综上可知，X=X↑↓，即X在细粒度实值形式背景中也是某一L-实概念的外延。

性质2表明，在多粒度实值形式背景中，细粒度实值形式背景的L-实概念的个数比粗粒度实值形式背景的L-实概念的个数多，这是因为在粗粒度实值形式背景中满足“主要小于”关系的对象在细粒度实值形式背景中可以不满足“主要小于”关系。即在粗粒度实值形式背景下不能形成L-实概念的序对在细粒度实值形式背景中有可能形成L-实概念。

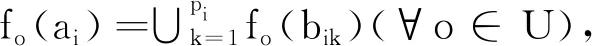
即对于粗粒度实值形式背景的L-实概念，它的每个实值属性ai的可能取值是细粒度实值形式背景中对应的特化属性可能取值的并。

性质3表明，多粒度实值形式背景的各个单粒度实值形式背景的L-实概念之间可以相互转化，即可以由粗粒度空间中的L-实概念拆分得到细粒度层的L-实概念，也可以由细粒度空间中的L-实概念合并得到粗粒度空间的L-实概念。依据上述性质，下面给出一个由细粒度实值形式背景的L-实概念得到粗粒度实值形式背景的L-实概念的算法。

算法1 计算粗粒度实值形式背景的L-实概念

输出：粗粒度实值形式背景的L-实概念Q。

初始化Q=∅；

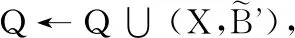
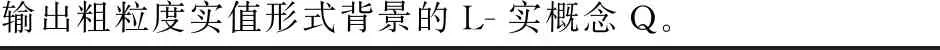
输出粗粒度实值形式背景的L-实概念Q。

例2对于例1中的多粒度实值形式背景，第1和第2粒度层下的实值形式背景的概念格分别如图3和图4所示，其中节点的详细信息见表4和表5。

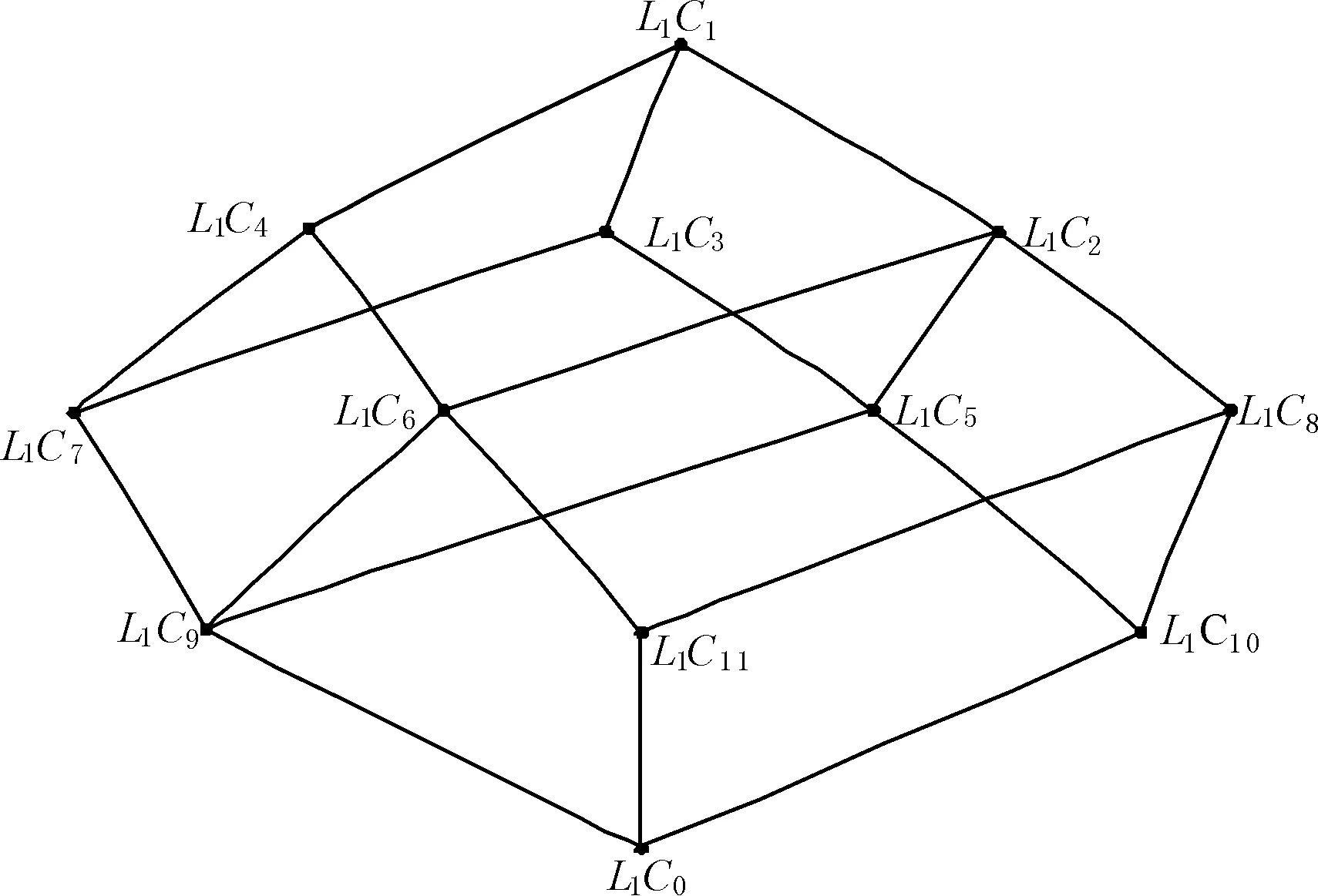
图3 表1的实值形式背景的概念格

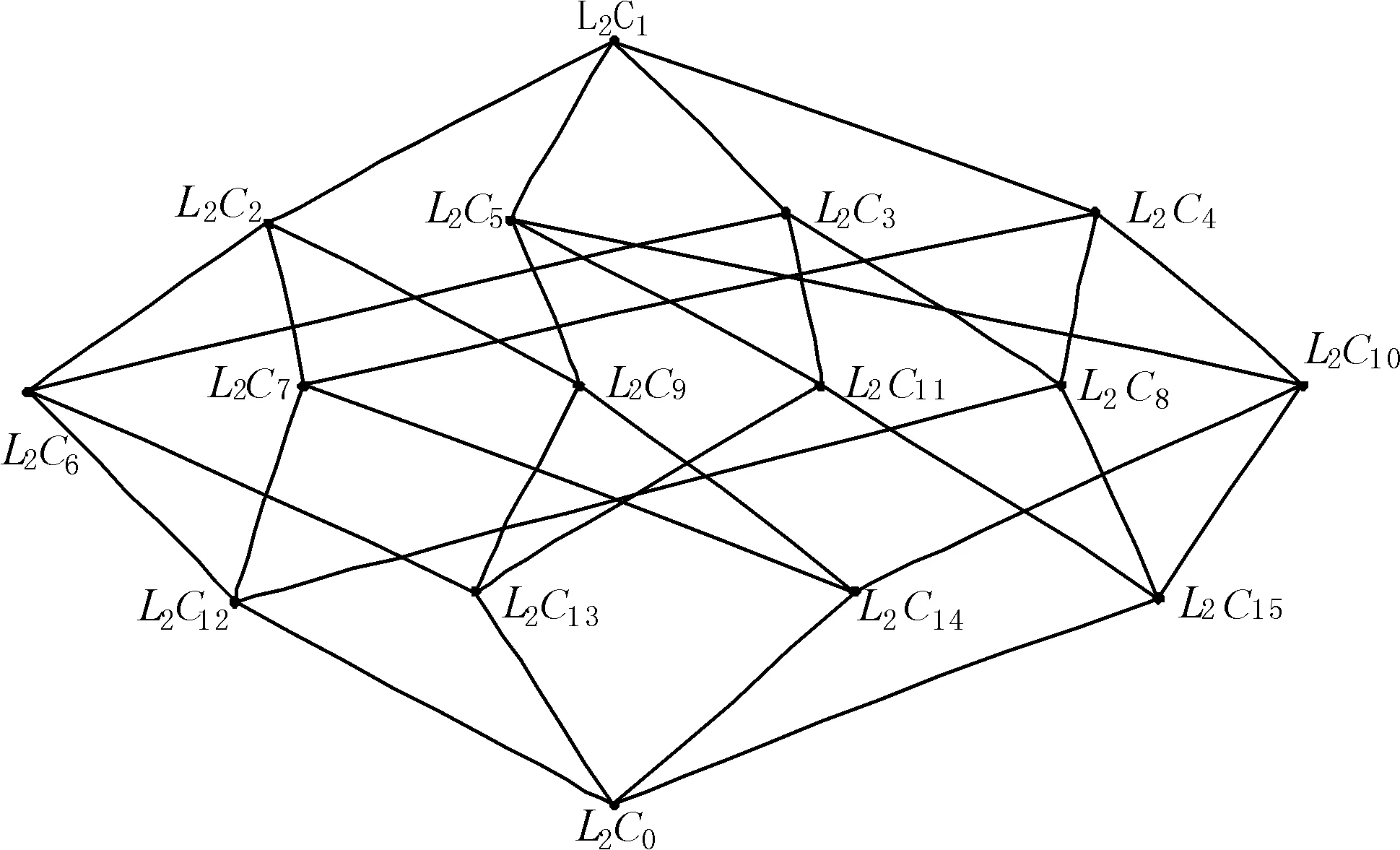
图4 表2的实值形式背景的概念格

表4 表1的所有L-实概念

表5 表2的所有L-实概念

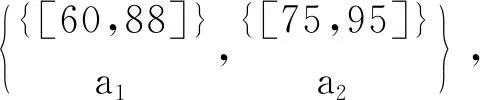
3 多粒度实值决策形式背景的知识发现

本节进一步将决策属性引入多粒度实值形式背景中，讨论多粒度实值决策形式背景各粒度层下决策规则之间的联系。

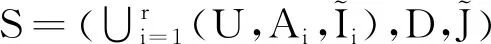
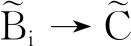
表6 实值形式背景

图5 表6的实值形式背景的概念格

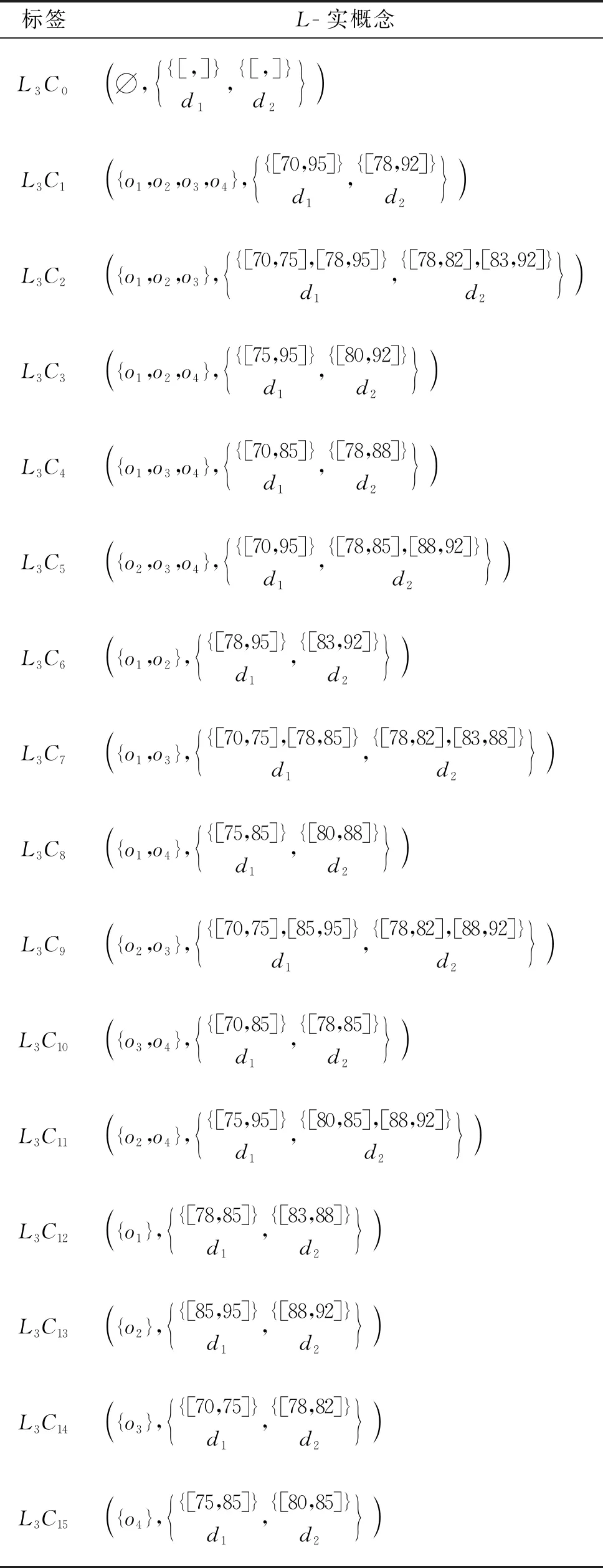
表7 表6的所有L-实概念

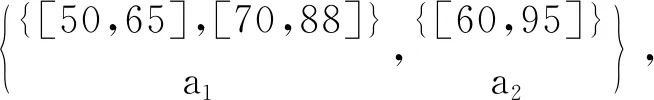
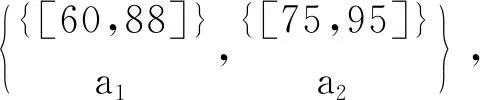
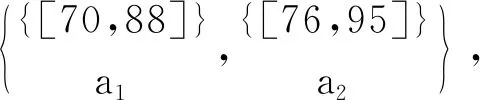
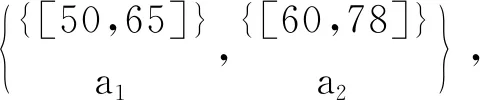
4 结语

本文将多粒度思想引入实值形式概念分析中，提出了多粒度实值形式背景，研究了L-实概念与L-实决策规则随着粒度空间粗细变化的转移或演化规律。有关多粒度实值概念与决策规则的结论，既完善了实值概念格理论，又推广了现有的多粒度形式概念分析方法。

一方面，在粒度空间从粗到细的变化过程中，尽管可以使得数据分析更加具体化，但是计算复杂度也会相应增加，因此需要继续研究L-实概念与L-实决策规则的演化效率；另一方面，在粒度空间从细到粗的变化过程中，信息会丢失，从而影响L-实概念与L-实决策规则的有效性，所以有待进一步给出多粒度实值形式背景的信息度量方法以及L-实概念与L-实决策规则的有效性评估方法。

另外，为了进一步对多粒度实值形式概念分析理论与方法进行完善，仍需考虑将实值类属性块推广到多粒度实值类属性块，即允许条件概念的实值属性信息来源于不同的粒度空间，从而使得L-实概念与L-实决策规则的知识发现实现深层次的跨粒度层组合。

最后，需要指出的是，本文的讨论均针对L-实概念展开。然而，对于实值形式概念分析，除了L-实概念，还有另一种实概念(即S-实概念)，本文未考虑S-实概念的研究情况，主要原因是它将有类似的结论成立，故没有平推式列出相应的结论。