自适应设计广义线性模型的自适应Lasso惩罚最小二乘的渐近性质
高启兵,于 欢,时倩倩,朱桂梅
(南京师范大学 数学科学学院, 江苏 南京 210046)
广义线性模型同时适用于连续和离散数据分析,其应用范围比正态线性模型更广泛,在生物、医学、社会和经济金融等领域有重要应用,所以自Nelder和Wedderburn提出该模型以来就一直备受相关学者关注[1]。有关广义线性模型统计推断的渐近理论研究可参见文献[2-9]。
变量选择是近代回归分析中的热点问题。在实际应用中,研究者通常收集较多相关变量,但只有部分是显著有用的。如果将过多不显著的变量用于统计建模,会降低模型的有效性及可解释性,同时可能得出错误的结论。因此,变量选择在各类统计建模中具有重要作用。传统的变量选择方法有逐步回归和最优子集方法,但它们都有一些局限性,如缺乏稳定性等。近年来,基于惩罚的变量选择方法被应用于各类统计模型,且备受关注。如Tibshirani提出的Lasso惩罚方法[10],其具有能同时进行变量选择和参数估计的特性;Fan等在指出Lasso方法的一些不足之后,提出能同时具有变量选择及参数估计的Scad惩罚方法,该方法具有稀疏性、连续性、相合性及Oracle性质[11]。其他惩罚方法还有 Frank等提出的桥惩罚方法[12]、Zou等提出的具有分组效应的弹性网惩罚方法[13]及Zhang提出的MCP凹惩罚方法等[14]。由于Lasso方法在某些情况下是不相合的,Zou为了改进Lasso方法而提出了自适应Lasso方法,并且还证明了自适应Lasso具有Oracle性质[15]。近年来,也有关于广义线性模型基于惩罚方法的变量选择方法研究:Wang等考虑了桥惩罚估计方法及其性质[16];Wang等研究Lasso和组Lasso方法的渐近性质[17];Cui等探讨基于拟似然的桥惩罚估计的渐近性质[18];Cui等讨论自适应Lasso惩罚最小二乘估计的渐近性质[19];陈夏等考虑自适应Lasso拟似然估计的渐近性质等[20]。但是,他们考虑的都是独立数据或固定设计下的广义线性模型,不适应于自适应设计广义线性模型,即具有时间序列成分或一定相依结构的动态数据广义线性模型分析。本文将对自适应设计广义线性模型的自适应Lasso惩罚最小二乘方法的渐近性质进行探讨。
1 模型与主要结果
假设观测数据为{(yi,Xi),i=1,2,…,n},满足
式中:yi是一维响应变量;Xi是q维设计向量;β=(β1,β2,…,βq)T为未知的q-维参数,具有真值β0;μ(·)为已知的均值函数;Fi-1是由{(yi,Xj),j=1,2,…,i-1}生成的σ-域,Xi关于Fi-1可测,即设计向量由历史数据而定。
以上模型称为自适应设计广义线性模型,对该模型的研究主要应用极大拟似然方法,有关参数极大拟似估计的渐近理论参考文献[4,9,21]等。
为进行参数估计和变量选择,考虑以下自适应Lasso惩罚最小二乘目标函数:
(1)
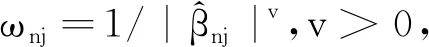
式中Θn是参数空间。
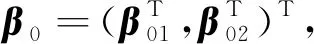
为获得本文的结果,需要下列假设条件。
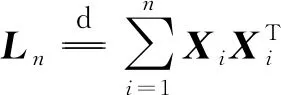
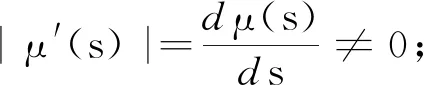

下面给出在自适应设计下自适应Lasso惩罚最小二乘的渐近性质。
定理1若条件C1~C5满足,则有
定理2若条件C1~C5满足,则当n→∞时有
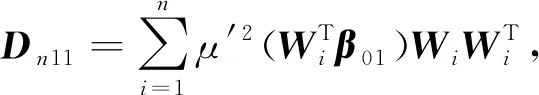
2 数值模拟
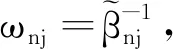
在模拟中,生成N=200组数据集,每组数据集都包含n个观测数据。在自适应设计下考虑以下Logistic回归模型:
式中β0是11维的向量,设β01=1,β02=1,β05=0.8,β08=-1,其余分量均为0。考虑2种不同的样本量:n=200和n=400。协变量Xi=(1,ui,yi-1,yi-2,yi-3,yi-4),其中第一项是截距项,ui是服从均值为0、方差为1且第(i,j)个元素的协方差是r|i-j|的6维多元正态分布,其中对于r也考虑了2种情况:r=0.2和r=0.4。
为了对比不同方法在模型选择上的性能优劣,计算以下模型误差ME(式中简记为er):
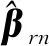
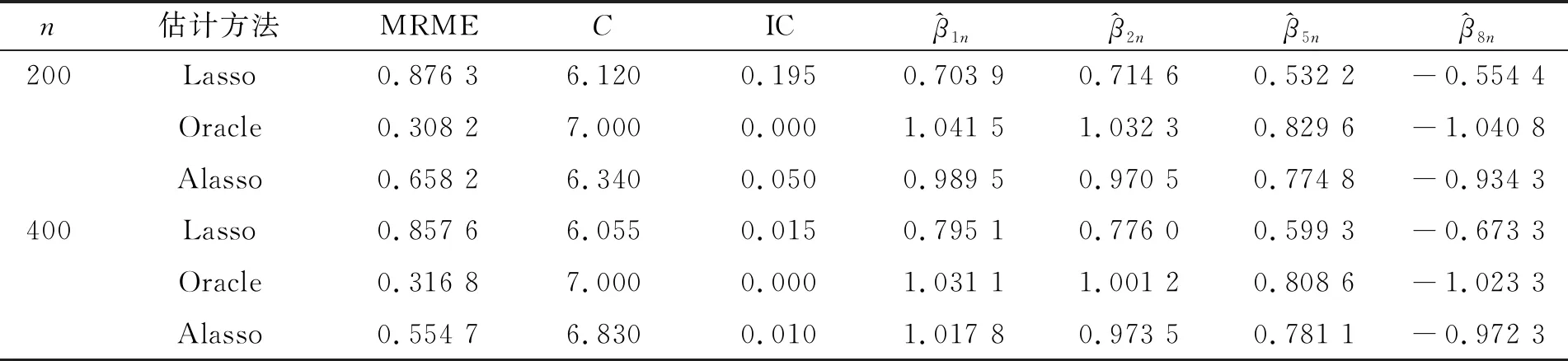
表1 Logistic模型中MRME、(C,I)以及参数估计值的比较(r=0.2)
通过模拟研究,可得以下结论。
1)自适应Lasso产生的模型的MRME比Lasso要小,与Lasso方法相比,自适应Lasso估计选择的零系数的数目接近真实值,这与定理3的变量选择结果一致。
2)在参数估计上自适应Lasso估计也要优于Lasso方法,尤其是对自适应设计部分非零参数的估计,自适应Lasso估计值更接近真实值。随着样本数的增多,自适应Lasso参数估计的精度明显提高。
3 主要结果证明
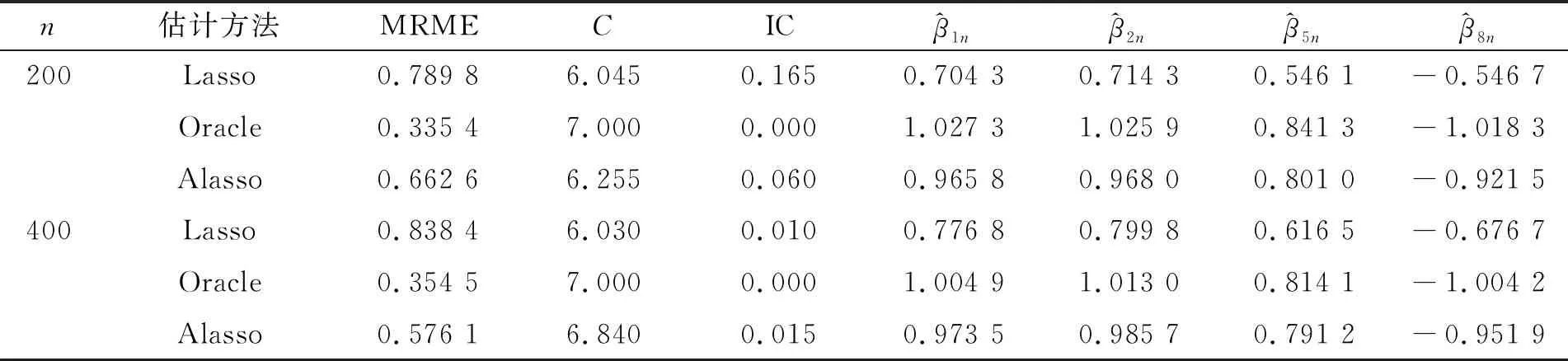
表2 Logistic模型中MRME、(C,I)以及参数估计值的比较(r=0.4)
为证明本文结果,需要以下引理。
引理1假设条件C1~C4成立,则有
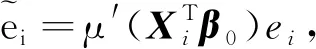
证明令uk和ul是q维单位向量,且它们的第k个和第l个分量分别为1。因为{ei,i=1,2,…}是一个鞅差,并且Xi是Fi-1可测的,所以
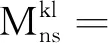
s=1,2,…,n
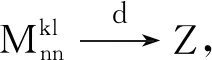
引理2假设条件C1~C4成立,则有
式中C是一个正常数。
证明令βu=β0+αnCu。经过计算,可以把Wn(β)分为4个部分。首先,
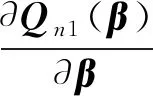
然后对上式求导可得
Wn(βu)=-An(βu)-Bn+Cn(βu)+Vn(βu)。
式中:
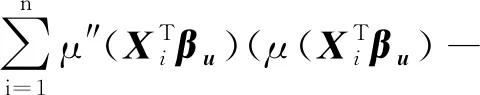
从而有
πn3(βu)+πn4(βu)。
式中:
根据条件C1可知当n→∞时,有
由C1和C3,有
由C3,有
因此,可以推出
同理,可以类似地证明
经过计算不难看出,
根据引理1,‖Mn‖=op(1),由条件C3知‖Nn‖=O(1)。从而有
类似地,可以证明
综上,可以推断出
πn2+πn3(βu)+πn4(βu)‖≤
‖πn1(βu)‖+‖πn2‖+‖πn3(βu)‖+
‖πn4(βu)‖=op(1)。
故引理2得证。
引理3假设条件C1~C5成立,则有
证明根据Ln(β)定义,有
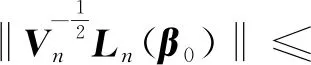
Op(1)。
故引理3得证。

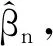
不妨令
[Qn1(β0+αnCu)-Qn1(β0)]+
式中:
Ψn1=[Qn1(β0+αnCu)-Qn1(β0)];
要证明定理1,只要证明这2部分在‖u‖=1上均一致大于0即可。对于Ψn1,2次应用积分中值定理有
Ψn1=Qn1(β0+αnCu)-Qn1(β0)=
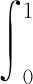
Ln(β0)]dt1=αnCuTLn(β0)+
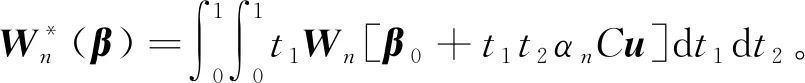
根据引理3可知
再由引理2有
所以有
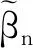
综上所述,∀ε>0,当C取足够大时就可以以大于1-ε的概率使得Ψn1+Ψn2>0。定理1得证。
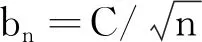
式中i=t+1,…,q。
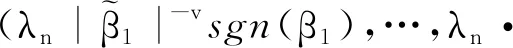
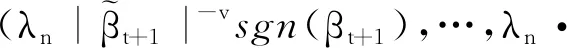
应用积分中值定理,有

(β-β0)+F2(β2)。
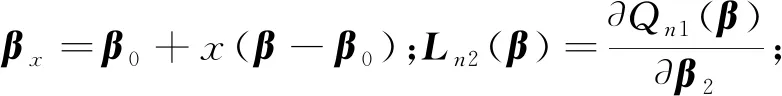
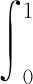
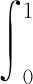
式中1q-t是一个分量全是1的q-t的维向量。根据引理3以及c1nIq≤Vn≤c2nIq可知
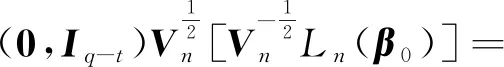
因此,
即
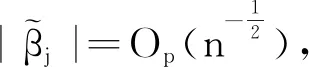


即
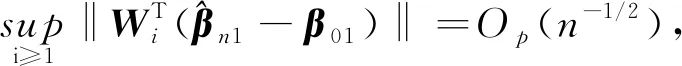
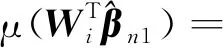
β01)+Op(n-1/2),
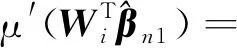
β01)+Op(n-1/2)。
把以上2式代入前一个式子,可得
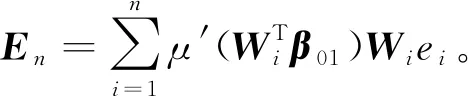
另一方面,根据条件C1~C3,易得c1nIt≤Sn≤c2nIt,从而结合条件C5及ωnj的定义有
综上所述,可得
定理3得证。
4 结论
本文在已知均值结构的前提下,研究自适应设计下广义线性模型自适应Lasso惩罚最小估计的渐近性质。在一定条件下,可以得到自适应 Lasso惩罚最小二乘估计的相合性和Oracle性质。该结果将固定设计的广义线性模型的变量选择问题推广到自适应设计的广义线性模型中,为动态观测数据(如时间序列数据)的分析提供理论保障。最后,通过模拟显示,同Lasso惩罚及Oracle方法的结果进行对比,自适应Lasso惩罚方法要优于Lasso惩罚方法并接近Oracle方法。

