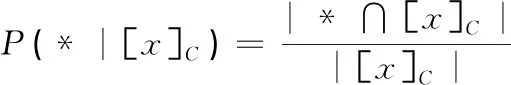单值中智信息下的一种新型三支决策模型

杨海龙,任欢欢,焦 丽

(陕西师范大学 数学与统计学院, 陕西 西安 710119)

三支决策理论[1]是处理决策问题的一种新的思想方法论。 Yao利用TAO模型来描述和解释三支决策, 其中符号“T”“A”和“O”分别指三支决策的3个层次[2]。 第1层是“三分”：将一个论域划分为三个互不相交的部分, 即正域、负域和边界域。 第2层是“治”：提出这3部分相对应的策略。 第3层是“效”：对前2层给出的3分和策略的好坏进行评价。

三支决策的研究包括理论、模型和应用研究, 发展迅速。 在理论方面, Hu提出了三支决策空间的概念[3]；Yao从集合论的角度讨论了三支决策[4]。 在模型方面, Zhang等研究了两类分类错误的三支决策模型[5]。Li等将单论域上的三支决策模型[6]推广到双论域[7]； Li等进一步研究了0-1信息表上的三支决策模型[8]。 在应用方面,Zhou等提出了一种基于三支决策的方法来降低垃圾邮件过滤过程中误分类的错误率[9]；Liu等在序决策系统中构建了一个三支决策模型来优化薪酬管理方法[10]。

中智集[11-12]作为直觉模糊集[13]的推广, 在处理不确定和不精确信息时更具有普适性。 众多研究者在中智集理论和应用方面做了深入研究。特别是关于中智集和三支决策的融合研究, 引起了国内外研究者的关注。Abdel-Basset等通过使用评价函数成功地将三支决策与单值中智集结合并给出了资源选择问题的AHP-QFD框架[14]。Singh利用中智集研究了三支概念格的表示方法[15]。 此外,Singh研究了不同粒度下的三支n值中智概念格[16]。Jiao等在单值中智信息下基于余弦相似度和欧氏距离提出了两种三支决策模型, 并给出了模型的应用[17]。本文进一步开展此研究, 利用单值中智数的计分函数和精确度函数, 基于贝叶斯决策理论提出一种新型三支决策模型。

1 预备知识

1.1 单值中智集与单值中智数

定义1[11-12]设U是一个论域。U上的单值中智集A由正确隶属函数TA、不确定隶属函数IA和错误隶属函数FA构成,其中∀x∈U,TA(x),IA(x),FA(x)∈[0,1]。U上的单值中智集A可以表示为

A={〈x,TA(x),IA(x),FA(x)〉:x∈U}。

∀x∈U,称(TA(x),IA(x),FA(x))为一个单值中智数。 在不致混淆的情况下, 一个单值中智数n可表示为n=(Tn,In,Fn)。

常见的单值中智数的比较方法有以下两种。

定义2[11]设n=(Tn,In,Fn)和m=(Tm,Im,Fm)是两个单值中智数，若Tn≤Tm,In≥Im,Fn≥Fm，则称n小于等于m,记作n⪯m。

定义3[18]设n=(Tn,In,Fn)和m=(Tm,Im,Fm)为两个单值中智数，若Tn≤Tm,In≤Im,Fn≥Fm，则称n小于等于m，记作n⪯m。

定义2和定义3给出的两种排序方法的不同之处是对不确定隶属度的处理不同,均存在一些不足。 首先,它们并不能比较任意两个单值中智数。 例如,取n=(0.3,0.5,0.2),m=(0.5,0.7,0.9),则不论利用定义2还是定义3,n和m都不可比较。 其次,文献[19]指出定义2和定义3是两种极端情况,并通过例子阐述了这两种排序方法都没有充分体现不确定隶属函数IA的作用。 进一步,提出了一种新的单值中智数排序方法[19]。

为了给出单值中智数新的排序方法, 文献[19]首先引入了单值中智数的计分函数和精确度函数概念。

定义4[19]设集合D*={x=(x1,x2,x3)|x1,x2,x3∈[0,1]}，定义函数s为

s:D*→[0,1],∀n=(Tn,In,Fn)∈D*,

称s为单值中智数的计分函数。

定义函数h为

h:D*→[0,1],∀n=(Tn,In,Fn)∈D*,

称h为单值中智数的精确度函数。

基于计分函数和精确度函数,文献[19]提出了一种新的单值中智数排序方法。

定义5[19]设n=(Tn,In,Fn)和m=(Tm,Im,Fm)是两个单值中智数。

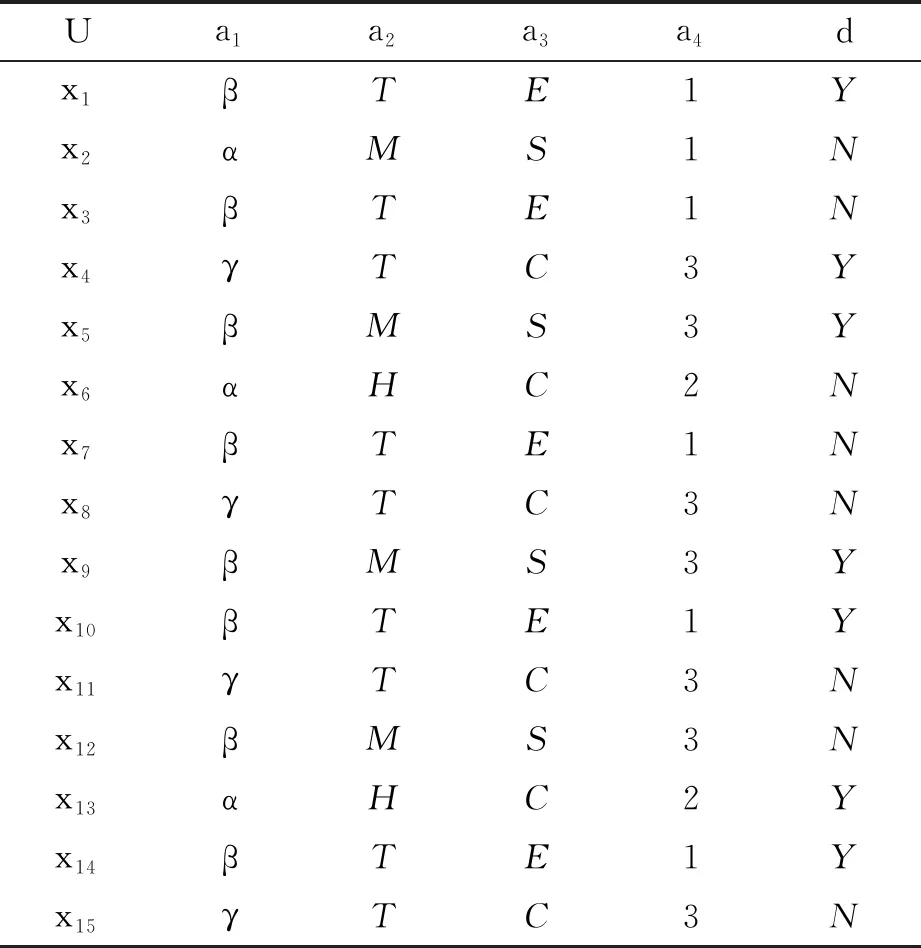
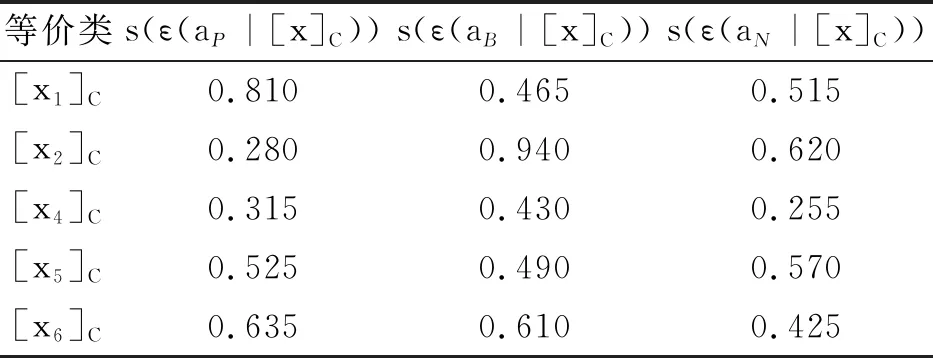
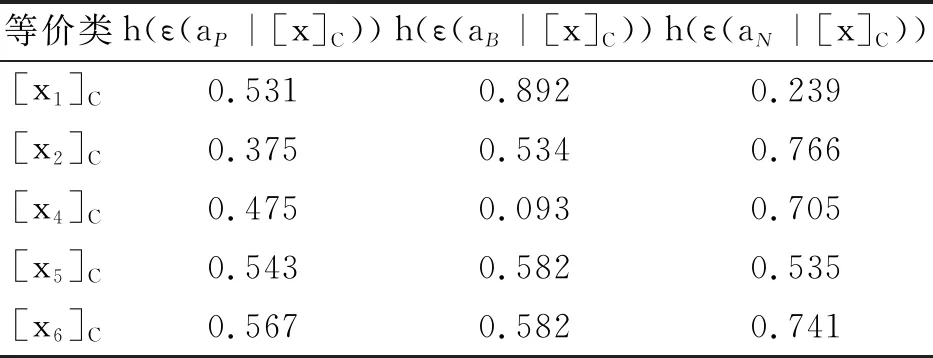
1)若s(n)

2)若s(n)=s(m),h(n)

3)若s(n)=s(m),h(n)=h(m),In

4)若s(n)=s(m),h(n)=h(m),In=Im，则称n等于m,记作n=m。

命题1[19]设n、m和p是3个单值中智数，则以下结论成立：

1)n⪯n;

2)若n⪯m且m⪯n，则n=m;

3)若n⪯m且m⪯p,则n⪯p;

4)若n⪯/m，则mn。

定义6[20]设n和m是两个单值中智数，θ是一个实数，其中θ>0，单值中智数的加法和数乘运算定义为

1)n⊕m=〈Tn+Tm-Tn·Tm,

In·Im,Fn·Fm〉;

2)θn=〈1-(1-Tn)θ,(In)θ,(Fn)θ〉。

1.2 三支决策

三支决策的核心思想是将论域U划分为3个两两不相交的部分, 即正域、负域和边界域。这3个域分别表示为Pos(U)、Neg(U)和Bnd(U)。正域、边界域和负域分别确定三分类中接受、不承诺和拒绝的决策规则。三支决策在解决问题和处理信息方面发挥着重要作用。

下面以2个状态来阐述基于贝叶斯决策过程的三支决策。 设Ω={X,┐X}是状态集,A={aP,aB,aN}是行动集,其中,状态集Ω中的X和┐X分别表示对象x(x∈U)属于状态X和不属于状态X，行动集A中的aP,aB,aN分别表示对x采取的3个行动，即决定x∈Pos(X),x∈Bnd(X),x∈Neg(X)。

在表1中,λPP、λBP和λNP分别表示当对象x属于X时，采取aP、aB和aN这3种行动带来的损失。同样地，λPN、λBN和λNN分别表示当对象x不属于X时，采取aP、aB和aN这3种行动带来的损失。

表1 损失函数

采取这3种不同行为所产生的期望损失可以表示为ε(a·|[x])(·=P,B,N)，具体如下：

ε(aP|[x])=λPPP(X|[x])+λPNP(┐X|[x]),

ε(aB|[x])=λBPP(X|[x])+λBNP(┐X|[x]),

ε(aN|[x])=λNPP(X|[x])+λNNP(┐X|[x])。

根据贝叶斯决策理论，得到以损失最小为依据的决策规则如下：

(P)当ε(aP|[x])≤ε(aB|[x])且ε(aP|[x])≤ε(aN|[x])，则x∈Pos(X);

(B)当ε(aB|[x])≤ε(aP|[x])且ε(aB|[x])≤ε(aN|[x]),则x∈Bnd(X);

(N)当ε(aN|[x])≤ε(aP|[x])且ε(aN|[x])≤ε(aB|[x])，则x∈Neg(X)。

2 单值中智信息下基于计分函数和精确度函数的三支决策模型

Jiao等基于余弦相似度和欧氏距离给出了单值中智信息下2种三支决策模型[17],本节基于计分函数和精确度函数给出单值中智信息下的一种新型三支决策模型。

在单值中智信息下, 损失函数是单值中智数的形式, 如表2所示。对于X中的对象x,采取行动aP、aB和aN的期望损失为

表2 带有单值中智信息的损失函数

ε(aP|[x])=λPPP(X|[x])⊕λPNP(┐X|[x]),

ε(aB|[x])=λBPP(X|[x])⊕λBNP(┐X|[x]),

ε(aN|[x])=λNPP(X|[x])⊕λNNP(┐X|[x])。

由定义6可得

ε(aP|[x])=λPPP(X|[x])⊕λPNP(┐X|[x])=

(TλPP,IλPP,FλPP)P(X|[x])⊕

(TλPN,IλPN,FλPN)P(┐X|[x])=

(1-(1-TλPP)P(X|[x]),(IλPP)P(X|[x]),

(FλPP)P(X|[x])⊕(1-(1-TλPN)P(┐X|[x]),

(IλPN)P(┐X|[x]),(FλPN)P(┐X|[x]))=

(TεP,IεP,FεP)。

(1)

式中：

TεP=1-(1-TλPP)P(X|[x])(1-TλPP)P(┐X|[x])；

IεP=(IλPP)P(X|[x])(IλPN)P(┐X|[x])；

FεP=(FλPP)P(X|[x])(FλPN)P(┐X|[x])。

类似地，

ε(aB|[x])=(TεB,IεB,FεB),

(2)

ε(aN|[x])=(TεN,IεN,FεN)。

(3)

式中:

TεB=1-(1-TλBP)P(X|[x])(1-TλBN)P(┐X|[x]),

IεB=(IλBP)P(X|[x])(IλBN)P(┐X|[x]),

FεB=(FλBP)P(X|[x])(FλBN)P(┐X|[x]);

TεN=1-(1-TλNP)P(X|[x])(1-TλNN)P(┐X|[x]),

IεN=(IλNP)P(X|[x])(IλNN)P(┐X|[x]),

FεN=(FλNP)P(X|[x])(FλNN)P(┐X|[x])。

显然，ε(a·|[x])(·=P,B,N)都是单值中智数。

由定义5和决策规则(P)—(N)，可得

(P1)若s(ε(aP|[x]))

或s(ε(aP|[x]))=s(ε(aB|[x])),

h(ε(aP|[x]))

或s(ε(aP|[x]))=s(ε(aB|[x])),

h(ε(aP|[x]))=h(ε(aB|[x])),IεP≤IεB;

以及s(ε(aP|[x]))

或s(ε(aP|[x]))=s(ε(aN|[x])),

h(ε(aP|[x]))

或s(ε(aP|[x]))=s(ε(aN|[x])),

h(ε(aP|[x]))=h(ε(aN|[x])),IεP≤IεN成立；

则x∈Pos(X);

(B1)若s(ε(aB|[x]))

或s(ε(aB|[x]))=s(ε(aP|[x])),

h(ε(aB|[x]))

或s(ε(aB|[x]))=s(ε(aP|[x])),

h(ε(aB|[x]))=h(ε(aP|[x])),IεB≤IεP;

以及s(ε(aB|[x]))

或s(ε(aB|[x]))=s(ε(aN|[x])),

h(ε(aB|[x]))

或s(ε(aB|[x]))=s(ε(aN|[x])),

h(ε(aB|[x]))=h(ε(aN|[x])),IεB≤IεN成立；

则x∈Bnd(X);

(N1)若s(ε(aN|[x]))

或s(ε(aN|[x]))=s(ε(aP|[x])),

h(ε(aN|[x]))

或s(ε(aN|[x]))=s(ε(aP|[x])),

h(ε(aN|[x]))=h(ε(aP|[x])),IεN≤IεP;

以及s(ε(aN|[x]))

或s(ε(aN|[x]))=s(ε(aB|[x])),

h(ε(aN|[x]))

或s(ε(aN|[x]))=s(ε(aB|[x])),

h(ε(aN|[x]))=h(ε(aB|[x])),IεN≤IεB成立；

则x∈Neg(X)。

根据上述过程, 由给定的决策表可得对象的2个状态, 进一步计算出条件概率。在给出损失函数的情况下, 得到期望损失。然后通过计分函数和精确度函数比较期望损失, 得到三支决策规则。 对此过程进行总结, 得到以下算法步骤。

算法1单值中智信息下基于计分函数和精确度函数的三支决策。

第一步给定决策表(U,C∪D,V)，其中对象集U={x1,x2,…,xn}，条件属性集C={a1,a2,…,am}，决策属性集D={d}，V是属性值集。根据决策属性得到对象的2个状态X和┐X，及等价类[x]C，其中[x]C是由C确定的x的等价类,[x]C={y∈U|Cai(x)=Cai(y),i=1,2,…,m}，Cai(x)是x关于属性ai的属性值。

第三步由式(1)～(3)计算出每个等价类的期望损失ε(a·|[x]C)(·=P,B,N)。

第四步由定义4计算出每个期望损失对应的计分函数和精确度函数。

第五步根据决策规则(P1)～(N1)得到决策结果。

3 应用举例及比例

下面利用一个例子来阐述所提模型的有效性和可行性。

例1近年来,古董收藏越来越受大众欢迎。 一位古董爱好者欲购买一些古董, 设有15个可供选择的古董, 4 个条件属性, 1个决策属性。 为方便起见,令U={x1,x2,…,x15}表示15个可供选择的古董之集;C={a1,a2,a3,a4}表示4个条件属性之集, 其中a1表示市场价值,a2表示储存要求,a3表示购买价格,a4表示增值空间;D={d}，其中d是决策属性,表示“是否购买”。 设关于15个候选古董的决策表(U,C∪D,V)如表3所示, 每个属性的属性值的含义如下:

表3 15个候选古董的决策表(U,C∪D,V)

a1的属性值α、β、γ，分别表示高、中、低；

a2的属性值H、M、T分别表示苛刻、中等、宽松；

a3的属性值E、S、C分别表示贵、合适、便宜；

a4的属性值1、2、3分别表示大、一般、小；

d的属性值Y、N分别表示购买、不购买。

λ·Y和λ·N(·=P,B,N)分别表示在购买和不购买的情况下，采取行动aP、aB和aN造成的损失(见表4)。

表4 5个等价类对应的损失函数

由表3可以得到2个状态集：

X={x1,x4,x5,x9,x10,x13,x14},

┐X={x2,x3,x6,x7,x8,x11,x12,x15}

和每个对象xi的等价类为

[x1]C=[x1,x3,x7,x10,x14},

[x2]C={x2},

[x4]C={x4,x8,x11,x15},

[x5]C={x5,x9,x12},

[x6]C={x6,x13}。

表5 条件概率的值

ε(aP|[x1]C)=(0.86,0.23,0.24)。

类似地，可得对其他等价类中的对象采取不同行动的期望损失，如表6所示。

表6 等价类中的对象采取不同行动的期望损失

根据定义5, 可分别计算出每个期望损失的计分函数和精确度函数, 如表7和表8所示。

表7 期望损失的计分函数

表8 期望损失的精确度函数

显然,对于等价类[x1]C有s(ε(aB|[x1]C))

类似地,可以得到其他对象的决策结果:x2∈Pos(X);x1,x3,x5,x7,x9,x10,x12,x14∈Bnd(X);x4,x6,x8,x11,x13,x15∈Neg(X)。换言之,古董x2是个不错的选择, 应购买;古董x1、x3、x5、x7、x9、x10、x12和x14需要进一步考虑;古董x4、x6、x8、x11、x13和x15则不适合购买。

本文利用基于计分函数和精确度函数的排序方法比较单值中智数的大小, 从而比较采取各种行动的期望损失, 得到决策规则。相比于文献[17]中的模型，本文的模型更突出了单值中智数中不确定隶属度的意义。此外, 将本文提出的模型应用于文献[17]第4节中的例子, 可以发现所得的正域与文献[17]是相同的,即所推荐的对象是一样的。本文为单值中智信息下的三支决策问题提供了新思路和新方法。