基于快速凸无穷范数极小化的大量子空间的子空间分割
唐科威,穆梦娇,李缙红,张 杰,姜 伟,彭兴璇
基于快速凸无穷范数极小化的大量子空间的子空间分割
唐科威,穆梦娇,李缙红,张 杰,姜 伟,彭兴璇
(辽宁师范大学数学学院,辽宁 大连 116029)
子空间分割是计算机视觉和机器学习中的一个基本问题。由于实际问题中的数据往往类数较多,使得大量子空间的子空间分割问题显得尤为重要。近年来基于谱聚类的方法在子空间分割领域得到了越来越多的关注,但是在相关工作的实验中,子空间的个数却往往不超过10个。无穷范数极小化是近年来提出的一个专门针对大量子空间的子空间分割问题的方法,其通过降低表示系数矩阵的差异性能有效地处理该问题,但是仍有一定的局限,例如计算速度仍不够快,缺乏针对独立子空间问题的理论保证。为此,提出快速凸无穷范数极小化,该个方法不仅能够降低表示系数矩阵的差异性,而且能够对独立子空间情况提供理论保障且计算速度更快,大量的实验证明了该方法的有效性。
子空间分割;基于谱聚类的方法;大量子空间;无穷范数;快速算法
在大数据时代,数据的低维结构分析在许多实际应用中发挥着关键作用[1-6]。众所周知,在不同的光照条件下拍摄一个受试者的正面脸部图像,可以用一个低维子空间很好地刻画。事实上,该结构在许多其他应用中也存在,例如视频中刚体运动的轨迹特征点、不同形态的手写数字。不幸的是,一个单一的低维子空间通常不足以准确地刻画数据的几何结构,而多个子空间可以更好地刻画,因此需要面对子空间分割问题。给定一组采样于多个子空间并集的数据点,子空间分割的目的是将数据点划分为组,每个组对应一个子空间。子空间分割广泛应用于计算机视觉和机器学习领域,如图像分割[7-9]、运动分割[10]和人脸聚类[11]。现有的子空间分割方法大致可分为[12]迭代方法、统计方法、代数方法、基于谱聚类方法。基于谱聚类的方法是近年来的研究热点,该类方法首先寻找一个包含所有数据点之间相似度的亲和矩阵,然后对其应用归一化切割(normalized cut,NC)[13]来获得分割结果,而基于谱聚类方法的主要差别在于构造亲和矩阵的方式不同。
根据NC的原理,如果将亲和图构造为同一子空间获取数据点之间的权值大于不同子空间获得的数据点之间权值的形式,则分割效果较好。为了便于讨论,本文假设数据点的顺序与真实结果一致,此假设是不失一般性的,因为大多数基于谱聚类的方法都是全局最优的。在这种假设下,亲和矩阵的块对角结构引起广泛讨论。当子空间是独立的时候,很多方法都能得到块对角结构,例如低秩表示(low-rank representation,LRR)[14-15],最小二乘回归(least square regression,LSR)[16]和稀疏子空间聚类(sparse subspace clustering,SSC)[17-18]。为此,文献[16]和文献[19]还专门研究了目标函数满足一定的条件,就可以得到一个基于独立子空间假设的块对角结构,并且称这个条件为强制块对角结构(enforced block diagonal,EBD)条件。在子空间独立的情况下,满足EBD条件的前2条即可保证得到块对角结构。
实际应用中的数据集通常存在噪声和异常值,即使许多方法被设计成追求块对角的亲和矩阵,也不可避免非对角区域的元素是非零的。当子空间数量较多时,非对角噪声会严重影响分割性能。而在实际问题中,数据集往往包含很多类,因此面对大量子空间的子空间分割问题时,仅仅追求亲和矩阵的块对角结构是远远不够的。文献[20]表明,亲和矩阵中同类点对应的元素相互接近能在一定程度上克服上述非对角噪声带来的影响,本文称此性质为亲和矩阵的低差异性。其实,以往工作中探讨的很多性质都与亲和矩阵的低差异性有一定关系,例如聚组效应(grouping effect,GE)。
文献[21]表明,最小二乘回归(least square regression,LSR)[16]、光滑表示聚类(smooth representation clustering,SMR)[21]等方法具有GE。对于一组给定的高维数据点以及一个自表示矩阵,如果不同数据点间差异比较小,那么自表示矩阵中对应的列也趋于零,则该自表示矩阵具有GE[21]。因此,如果同一个子空间中的数据点相邻,则具有GE的块对角图在对角块上的差异较小。然而,这样的结果依赖于数据点的分布。对于任何数据集,都可以很容易地在相同的子空间中找到一些彼此之间距离很远的数据点,所以不能利用GE这个性质来准确地度量亲和矩阵的差异性。稠密块稀疏表示(dense block and sparse representation,DBSR)[22]的提出也考虑了亲和矩阵的低差异性。DBSR最小化自表示矩阵的1,1-范数和2-范数的组合,获得了稀疏性和稠密块性质的组合。由于最大奇异值可以是对角块差的一个界,因此可以诱导等密度块来实现亲和矩阵的低差异性。但是,该方法的计算速度对于大量子空间的子空间分割问题来说还不够快。无穷范数极小化(infinity norm minimization,INM)[20]是一个考虑了亲和矩阵低差异性的快速方法。该方法通过引入无穷范数控制对角块的差,对角块的差是指对角块的最大值减去最小值。因为矩阵的无穷范数不超过最大奇异值,所以相对于以往方法,该方法往往能够使亲和矩阵的差异性更低,从而对于大量子空间的子空间分割问题能获得更好的分割效果。但是INM不能满足EBD条件,因此无法在理论上保证亲和矩阵的块对角结构,同时在速度上也有上升的空间。
本文在INM的基础上提出了快速凸无穷范数极小化(fast convex infinity norm minimization,FC-INM)的方法来处理大量子空间的子空间分割问题,通过最小化无穷范数和1,1-范数的组合可以保证亲和矩阵的低差异性。在子空间独立的情况下,FC-INM能够满足EBD条件,从而在理论上保证了亲和矩阵的块对角结构。此外,受到文献[20]和文献[23]的启发,在求解FC-INM模型的过程中运用了一些加速技巧。实验结果表明,本文方法不仅计算速度高于INM,而且取得了较好的效果:
(1) 可以降低亲和矩阵的差异性,在大量子空间的子空间分割问题中取得了很好的效果;
(2) 在子空间独立的情况下,理论上可以保证获得的亲和矩阵具有块对角结构;
(3) 通过借鉴线性时间投影算法和Woodbury矩阵反演公式,本文方法的计算速度明显高于INM方法。实际上,本文方法的ADM算法比大多数基于谱聚类方法的ADM算法都快。
1 相关工作
1.1 符号说明
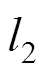
1.2 无穷范数极小化的回顾
为了便于理解,本文首先回顾INM子空间分割方法。记=[1,···,]为数据集,其中x(=1,···,)代表一个数据点,INM的模型为


根据先前工作的结果,INM的交替方向迭代(alternating direction method,ADM)[24]算法相对稳定。
算法1. INM的ADM算法。
输入:矩阵,参数。
输出:。
初始化:====0,=10-6,=1.1,=10-4。
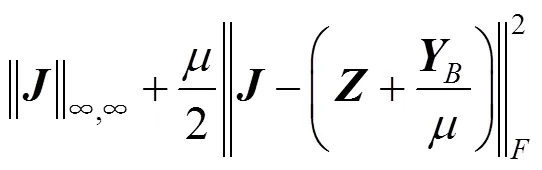
2 本文模型
INM虽然在子空间分割中取得了很好的效果,但是,在子空间独立的情况下,无法在理论上保证亲和矩阵的块对角结构,即不满足EBD条件的前2条。
已知函数(,)是定义在(,)上的,其中是由一些方阵组成的集合,是由非零列的方阵组成的集合。
假设所有矩阵都是兼容维数的,那么EBD的条件[16]为:
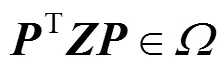
(2)(,)≥(,),当且仅当=或者3=4=0时,等号成立。
(3)(,)=(1,1)+(2,2)。
EBD条件(1)是子空间分割的基本要求,保证了分割结果对输入数据矩阵的列的任何排列都是恒定不变的。条件(2)是最小化函数后,在一定子空间假设下成为对角块的关键。条件(3)实际上没有要求函数的解是块对角的,但是通过此条件可以了解每个块的结构与所使用的函数之间的联系。

其中参数>0,用于控制亲和矩阵低差异性和稀疏性的平衡。
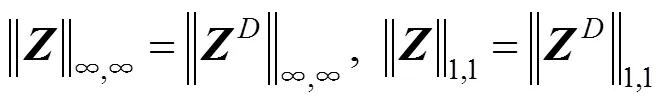
由此可见,本文模型满足EBD条件的前2点。
由命题2可知,当子空间独立时,本文方法计算的具备块对角结构。
考虑到实际应用中数据通常含有噪声,本文将式(2)中的模型改写为
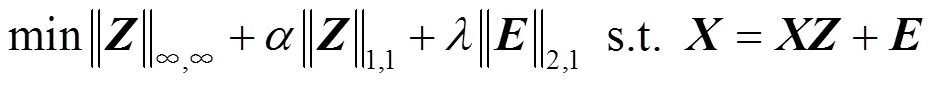
此外,通过对无穷范数相关问题采用了全新的求解方案,本文模型的数值算法还在计算速度上有所提高。在大量子空间的子空间分割问题中,数据量往往很大,所以此改进是尤为重要的。基于以上内容,本文方法称之为快速凸无穷范数极小化(fast convex infinity norm minimization,FC-INM)。
3 数值算法
为了便于无穷范数和1,1范数的求解,需要引入辅助变量和,则有
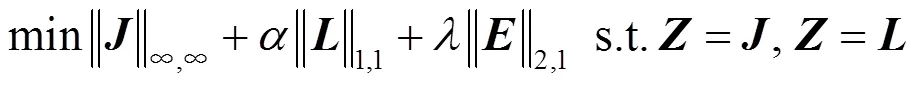
上述模型的增广拉格朗日函数为
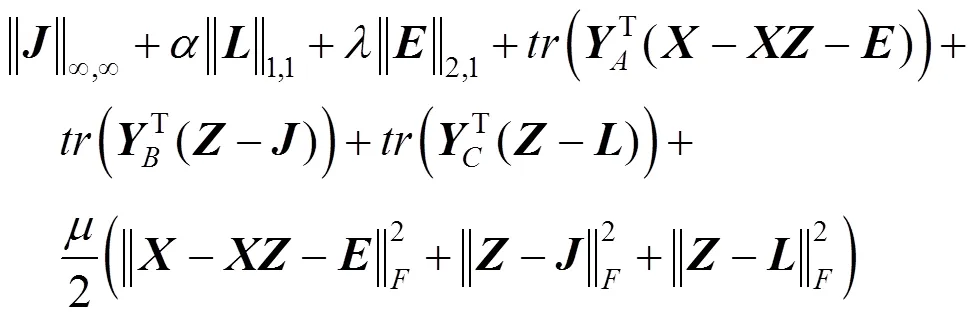
算法2. FC-INM的ADM算法。
输入:矩阵,参数和。
输出:。
初始化:=====0,=10-4,=1.5,=10-4。
算法2中的步骤2和步骤3,可以分别由文献[25]中的奇异值阈值算子和文献[14]中的引理3.2求解。根据经验,该算法的收敛性和稳定性都很好,但是算法2的主要计算量是步骤1和步骤4。
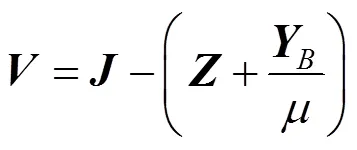
算法3.线性时间投影算法。
输入:,标量。
输出:。
步骤1.当非空时,随机从集合中选取一个索引。
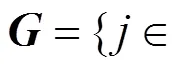
步骤4.设置,如果(+)-(+)(),=+,=+那么,为;否则,为{}。
若集合不为空,重复步骤1~4,直到为空集时,过程结束。
根据文献[23],该算法的算法复杂度为(2),低于INM算法中相关问题的算法复杂度。

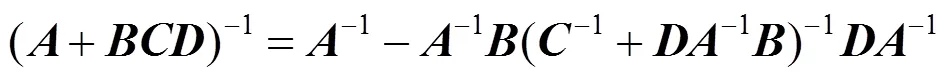
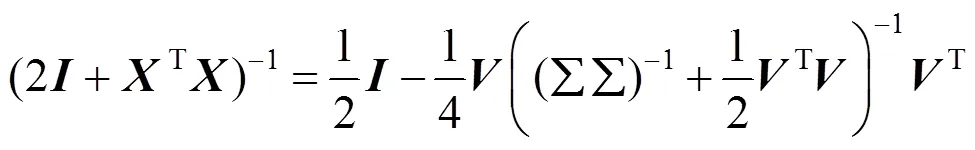
因此,算法2中的步骤4可以转化为

由于在迭代过程中不更新,和可以在循环外提前计算。
4 实 验
本文测试了FC-INM对于大量子空间的子空间分割问题的有效性。在2个基准数据库上与相关工作INM[20],LRR[14-15],SSC[17-18],LSR[16],SMR[21],DBSR[22]以及结构限制的低秩表示(structure constrained low-rank representation,SCLRR)[26]进行了比较,通过准确率(accuracy,ACC)、标准化互信息(normalized mutual information,NMI)和调整兰德指数(adjusted rand index,ARI)3个评价指标的百分比来评估性能,其中准确率为主要的评价指标。同时本文也对计算速度进行了比较。对于每种方法,都使用了原始作者提供的源代码,并对其重要参数进行了经验调优,从而获得最佳结果。
4.1 人脸聚类实验
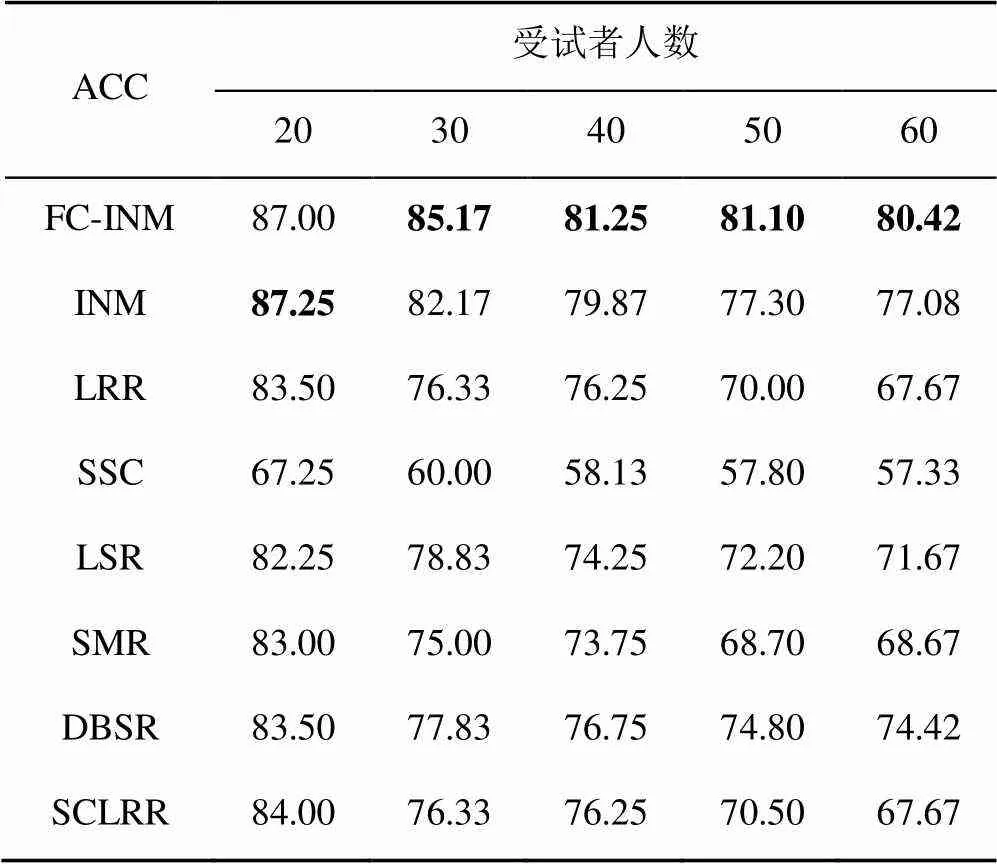
表1 每种方法在CMU PIE上的ACC (%)
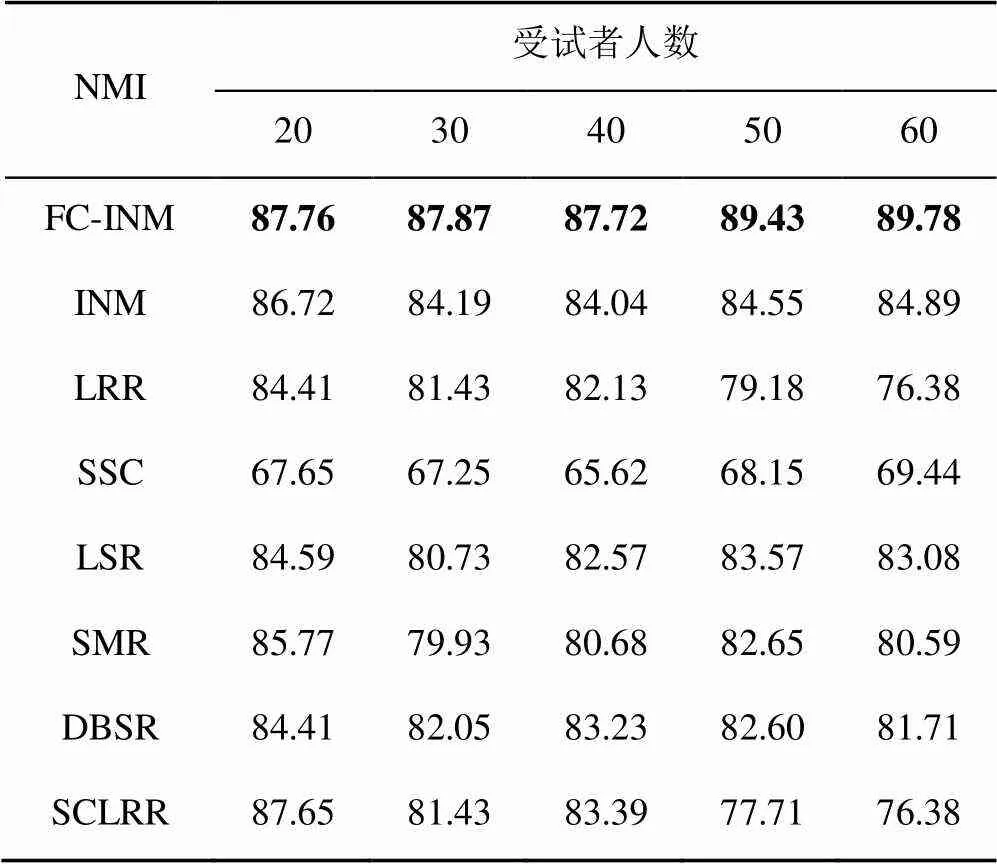
表2 每种方法在CMU PIE上的NMI (%)

表3 每种方法在CMU PIE上的ARI (%)

图1 FC-INM随参数变化的准确率
4.2 纹理聚类实验
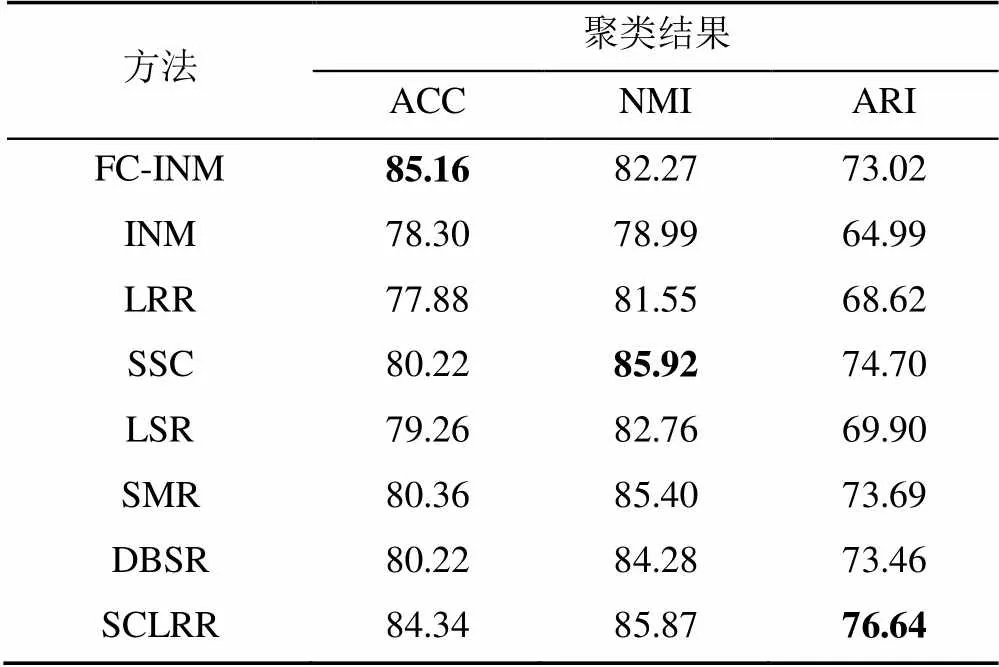
表4 每种方法在USC SIPI上的结果(%)
4.3 计算速度
大量子空间的子空间分割问题往往包含大量数据,所以计算速度在该问题中十分重要,在使用ADM迭代的方法中,INM已经是一个速度较快的方法。本文重点比较FC-INM与INM在上述实验数据上的计算速度。实验在一台I7-9700K处理器和16 G内存的计算机上进行,所有的时间都是以s为单位的。实验结果见表5,FC-INM较INM进一步提升了的计算速度,能够快速处理大量子空间的子空间分割问题,在实际问题中具有重要意义。

表5 两种方法的计算速度
5 结束语
本文提出了快速凸无穷范数极小化的子空间分割方法,该方法的一个重要优点是能够处理大量子空间的子空间分割问题,在实际问题中具有重要意义。各种基准数据库上的大量实验结果表明,本文方法可以保证亲和矩阵的低差异性,并且能够很好的进行大量子空间的子空间分割。然而,本文运用无穷范数控制对角块的差,只考虑了表示矩阵的全局性质,该策略也会在一定程度上缩小对角块处的元素与非对角块处元素的差异性。未来的工作,可以考虑表示矩阵的局部性质来克服上述局限性。
[1] ZHANG W, ZHANG Y M, MA L, et al. Multimodal learning for facial expression recognition[J]. Pattern Recognition, 2015, 48(10): 3191-3202.
[2] ZHANG W, QU C F, MA L, et al. Learning structure of stereoscopic image for no-reference quality assessment with convolutional neural network[J]. Pattern Recognition, 2016, 59: 176-187.
[3] ZHANG W, HU S N, LIU K. Patch-Based correlation for deghosting in exposure fusion[J]. Information Sciences, 2017, 415: 19-27.
[4] 唐科威, 由月, 苏志勋, 等. 核结构限制的低秩表示及其在流行聚类上的应用[J]. 计算机辅助设计与图形学学报, 2019, 31(4): 589-595. TANG K W, YOU Y, SU Z X, et al. Kernel structure constrained low rank representation for manifold clustering[J]. Journal of Computer-Aided Design & Computer Graphics, 2019, 31(4): 589-595 (in Chinese).
[5] 章荣, 陈谊, 张梦录, 等. 高维数据聚类可视分析方法综述[J]. 图学学报, 2020, 41(1): 44-56. ZHANG R, CHEN Y, ZHANG M L, et al. Overviewing of visual analysis approaches for clustering high- dimensional data[J]. Journal of Graphics, 2020, 41(1): 44-56 (in Chinese).
[6] 潘恒, 何进荣, 凌宇, 等. 基于多视图边界判别投影的高光谱图像分类[J]. 图学学报, 2018, 39(6): 1063-1068. PAN H, HE J R, LING Y, et al. Hyperspectral images classification based on multiview marginal discriminant projection[J]. Journal of Graphics, 2018, 39(6): 1063-106 (in Chinese).
[7] CHENG B, LIU G C, WANG J D, et al. Multi-task low-rank affinity pursuit for image segmentation[C]// 2011 IEEE International Conference on Computer Vision. Los Alamitos: IEEE Computer Society Press, 2011: 2439-2446.
[8] LANG C Y, LIU G C, YU J, et al. Saliency detection by multitask sparsity pursuit[J]. IEEE Transactions on Image Processing, 2012, 21(3): 1327-1338.
[9] YANG A Y, WRIGHT J, MA Y, et al. Unsupervised segmentation of natural images via lossy data compression[J]. Computer Vision and Image Understanding, 2008, 110(2): 212-225.
[10] RAO S, TRON R, VIDAL R, et al. Motion segmentation in the presence of outlying, incomplete, or corrupted trajectories[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(10): 1832-1845.
[11] HO J, YANG M H, LIM J, et al. Clustering appearances of objects under varying illumination conditions[C]//2013 IEEE Computer Vision and Pattern Recognition. Los Alamitos: IEEE Computer Society Press, 2003: 11-18.
[12] VIDAL R. Subspace clustering[J]. IEEE Signal Processing Magazine, 2011, 28(2): 52-68.
[13] SHI J B, MALIK J. Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 22(8): 888-905.
[14] LIU G C, LIN Z C, YU Y. Robust subspace segmentation by low-rank representation[C]// Proceedings of the 27th International Conference on Machine Learning. Madison: Omnipress, 2010: 663-670.
[15] LIU G C, LIN Z C, YAN S C, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1): 171-184.
[16] LU C Y, MIN H, ZHAO Z Q, et al. Robust and efficient subspace segmentation via least squares regression[C]// Proceedings of the European Conference on Computer Vision. Heidelberg: Springer, 2012: 347-360.
[17] ELHAMIFAR E, VIDAL R. Sparse subspace clustering[C]//Proceedings of the 12thComputer Vision and Pattern Recognition. Los Alamitos: IEEE Computer Society Press, 2009: 2790-2797.
[18] ELHAMIFAR E, VIDAL R. Sparse subspace clustering; algorithm, theory, and applications[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(11): 2765-2781.
[19] LU C Y, FENG J S, LIN Z C, et al. Subspace Clustering by Block Diagonal Representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(2): 487-501.
[20] TANG K W, SU Z X, LIU Y, et al. Subspace segmentation with a large number of subspaces using infinity norm minimization[J]. Pattern Recognition, 2019, 89: 45-54.
[21] HU H, LIN Z C, FENG J J, et al. Smooth Representation Clustering[C]//Proceedings of the 2014 IEEE Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society Press, 2014: 3834-3841.
[22] TANG K W, DUNSON D B, SU Z X, et al. Subspace segmentation by dense block and sparse representation[J]. Neural Networks, 2016, 75: 66-76.
[23] DUCHI J C, SHWARTZ S S, SINGER Y, et al. Efficient Projections onto the ℓ1-Ball for Learning in High Dimensions[C]//Proceedings of the 25th International Conference on Machine Learning. Madison: Omnipress, 2008: 272-279.
[24] LIN Z C, CHEN M M, MA Y. The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices[EB/OL]. [2018-06-24]. https://arxiv. org/abs/1009.5055.
[25] CAI J F, CANDÈS E J, SHEN Z W. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956-1982.
[26] TANG K W, LIU R S, SU Z X, et al. Structure-constrained low-rank representation[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(12): 2167-2179.
[27] SIM T, BAKER S, BSAT M. The CMU pose, illumination, and expression database[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(12): 1615-1618.
Large subspace number subspace segmentation via fast convex infinity norm minimization
TANG Ke-wei, MU Meng-jiao, LI Jin-hong, ZHANG Jie, JIANG Wei, PENG Xing-xuan
(School of Mathematics, Liaoning Normal University, Dalian Liaoning 116029, China)
Subspace segmentation is one of the fundamentals in computer vision and machine learning. Given the large number of categories in practical problems concerning the data set, it is of great significance to address the issue of large subspace number subspace segmentation. Although spectral clustering-based methods received more attention in the field of subspace segmentation, the subspace number in the past experiments was usually less than 10. The infinity norm minimization was a recently proposed method specially for large subspace number subspace segmentation. It could effectively address this problem by reducing the difference of the representation matrix, but there remained some limitations. For example, the computation speed was not fast enough, and there was no theoretical guarantee for the independent subspaces. Therefore, a method named fast convex infinity norm minimization was proposed. This method can not only reduce the difference of the representation matrix, but also provide the theoretical guarantee for the independent subspace and enhance the computation speed, which has been testified by a large number of experiments.
subspace segmentation; spectral clustering-based methods; large subspace number; infinity norm; fast algorithm
TP 391
10.11996/JG.j.2095-302X.2020060954
A
2095-302X(2020)06-0954-08
2020-04-07;
2020-07-16
7April,2020;
16July,2020
国家自然科学基金项目(61702243,62076115,61702245,61771229);辽宁省“兴辽英才计划”项目(XLYC1907169);辽宁省教育厅项目(L201783642);大连市青年科技之星项目(2019RQ033)
National Natural Science Foundation of China (61702243, 62076115, 61702245, 61771229); LiaoNing Revitalization Talents Program (XLYC1907169); Liaoning Educational Committee (L201783642); Program of Star of Dalian Youth Science and Technology (2019RQ033)
唐科威(1985-),男,辽宁沈阳人,副教授,博士,硕士生导师。主要研究方向为计算机视觉、机器学习等。E-mail:kwtang@lnnu.edu.cn
TANG Ke-wei (1985-), male, associate professor, Ph.D. His main research interests cover computer vision and machine learning. E-mail:kwtang@lnnu.edu.cn

