低复杂度的fMRI脑激活区定位的盲分离算法

陈安莹，吴海锋，李 栋

低复杂度的fMRI脑激活区定位的盲分离算法

陈安莹，吴海锋，李 栋

(云南民族大学电气信息工程学院，云南 昆明 650500)

功能磁共振成像(FMRI)是一种医学影像技术，由于具有非侵入性和较高的时空分辨率等优点现已被广泛应用于脑区定位。然而传统的FMRI信号分离算法复杂度太高，运行时间长，不利于FMRI技术更有效地应用于脑功能的研究。针对传统FMRI脑区分离算法的计算复杂度问题，提出了一种基于二阶哈达码变换的盲分离算法。先计算fMRI数据中血氧水平依赖(BOLD)信号的相关函数，然后对其进行特征值分解得到解混矩阵，以此实现激活脑区定位。由于哈达码只由1或-1构成，因此可减少BOLD信号相关矩阵计算的复杂度。仿真结果表明，相比高阶统计量的独立分量分析(ICA)和二阶统计量的傅里叶变换盲分离算法，该算法的计算时间分别只有其25%和50%，而定位误差却较为接近。

功能磁共振成像；盲分离；独立分量分析；二阶统计量的盲辨识；脑激活区

人类的大脑皮层可以根据功能划分成不同的区域，如视觉区、运动区等，若该区域遭受损伤，可通过医学影像技术对其进行定位，从而确定相应的治疗方案。由于功能磁共振成像(functional magnetic resonance imaging, fMRI)具有非侵入性和高空间分辨率等优点，近年来已成为医学成像中的常用脑区定位技术。

在传统fMRI激活脑区定位算法中，统计参数图(statistical parametric mapping，SPM)[1]是一种常用的方法，其利用统计检验方法对受试者的不同成像结果进行比较来寻找具有统计学意义的激活区。然而，该方法需要预先知道设计矩阵，当设计矩阵不确定时往往会影响最终的定位效果。独立分量分析(independent components analysis, ICA)算法[2]采用盲分离的方式，将脑区信号作为源信号分离出，相比SPM方法，ICA并不需要设计矩阵已知[3]。然而，ICA类盲算法通常需要计算高阶统计量，且需要较多的迭代次数以保证收敛，因此计算复杂度较高。二阶统计量的盲辨识(second order blind identifiability，SOBI)算法[4]仅需计算相关函数就能实现信号分离，不需要计算高阶统计量，复杂度相对较低。然而，由于fMRI的脑区信号具有稀疏性，其相关函数信息量不够丰富，因此影响了分离性能。频域的SOBI(frequency SOBI, f-SOBI)算法[5]对稀疏信号进行反傅里叶变换，然后再求相关函数，因此使得原信号经过变换后不再稀疏，保证了变换后的相关函数包含了较多源信息，从而提高了分离性能。

针对fMRI脑区定位盲分离的计算复杂度问题，本文提出了一种哈达码变换的二阶盲分离算法(h-SOBI)，由于哈达码变换矩阵只由1或-1构成，因此可降低相关函数计算复杂度，从而减少整个信号分离算法的计算量。实验中采用SimTB (simulation toolbox)[6]工具箱产生fMRI仿真数据和实测数据，分别给出了fastICA，f-SOBI和本文算法的分离结果。实验结果表明，本文算法的计算时间得到了有效的减少，而激活区的定位误差却与传统分离算法相似。

1 相关工作

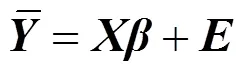
其中，为扫描时间点数；为设计矩阵；为解释变量；为残差。式(1)中，利用最小二乘准则估计，再对其做统计假设检验，即可推断脑区的激活情况。然而该方法需要预先知道设计矩阵的信息，否则就难以被估计。

SOBI算法首先计算信号的相关函数，令和-为的第列和第-列，那么R()的相关函数为

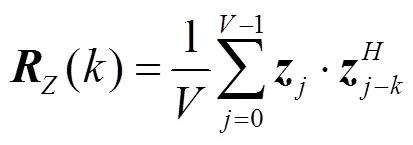
其中，Î{1,2,···,}为时延数。然后，通过联合对角化(joint diagonalization，JD)[10]获取解混矩阵。然而，由于fMRI数据具有稀疏性，其相关函数R()信息不够丰富，导致相关函数经联合对角化后难以获取较准确的解混矩阵。f-SOBI算法将观测信号进行反傅里叶变换后再求相关矩阵，变换后的相关函数第行和第列可表示为

2 问题提出

在fMRI数据分离算法中，第个被试者的BOLD信号矩阵(m)是一混合模型，省略字母后可表示为

由图1可知，观测数据其实是时间进程(time courses，TCs)与空间脑区映射(spatial maps，SMs)的乘积，而中的每一个脑区信号其实均为一稀疏的信号，经矩阵混合后得到的信号仍有可能为稀疏信号，若直接利用SOBI算法计算其相关函数[11]，会导致其包含的源信号信息不够丰富，从而难以较准确分离源信号。f-SOBI利用反傅里叶变换对fMRI数据进行反稀疏变换[11]，解决了稀疏的fMRI数据相关函数信息不够丰富的问题。然而，傅里叶变换的母函数为复数，与其相乘需要分别与实部和虚部各相乘一次。本文将从变换复杂度的问题出发，考虑另外一种变换方法，以减少乘法次数来降低计算复杂度。

图1 fMRI盲分离算线性混合模型

3 哈达码的二阶盲分离算法

3.1 相关函数

h-SOBI利用哈达玛变换来获取fMRI数据的相关函数，由于哈达码并不含有复数，且只由1或-1构成，因此在变换时只需与其实部相乘，而没有虚部，从而可减少乘法次数，其相关函数计算步骤如下。

x和y分别是经过哈达玛变换后的第行和第行中的第列元素，表示为

其中，u,j为×的哈达玛变换矩阵中第行第列元素，该哈达玛变换矩阵可表示为

其中，当=2时，哈达码矩阵为

由式(8)和(9)可知，哈达玛变换矩阵的元素是由1和-1构成的正交矩阵。

原相关函数R()经哈达玛变换后的第行和第列的相关函数可表示为

将式(6)和(7)代入式(10)中，可得

由于哈达玛变换矩阵是正交矩阵且元素之间满足以下关系

因此，式(11)可变为

其为利用哈达玛变换矩阵计算相关函数的表达式，由于式(13)中的u,k只有1或-1，因此可以减少相关函数求解过程的复杂度。

3.2 解混矩阵

从式(13)中获得解混矩阵，先要对相关矩阵进行联合对角化

以获取酉矩阵，其中，为联合对角化，则最后解混矩阵可通过

计算。其中，0为对信号进行白化的矩阵，(·)-1表示求逆。

3.3 h-SOBI的算法步骤

该算法先对数据进行PCA组降维，再求解降维后的数据的相关矩阵，然后通过联合对角化相关矩阵来获取解混矩阵，最后分离fMRI信号实现激活脑区的定位，具体算法如下：

输入：个被试的fMRI信号(m)，=1,2,···,。

步骤1.对fMRI信号进行PCA组降维和白化处理处理后得到；

步骤2.由式(13)得到的相关矩阵()；

步骤3.由式(14)联合对角化相关矩阵得到酉矩阵；

3.4 算法复杂度

4 仿真实验与分析

4.1 数据来源

本文的fMRI实验数据分别采用了仿真数据和实测数据。其中，仿真数据是由SimTB(Simulation Toolbox)工具箱仿真得到，该工具箱可在http:// mialab.mrn.org/software/simtb/index.html网站上下载，SimTB模拟创建30个脑区的fMRI数据，如图2(a)所示。实验中选取8个脑区作为源信号，如图2(b)所示。在创建fMRI数据的空间源过程中，将体素个数设置为=148×148，被试者数设置为=5，对比度噪声比(contrast to noise ratio，CNR)设置为模拟实际数据之间的空间差异性，每个被试者的脑区在正常范围内进行水平或垂直方向上的平移、旋转和扩展，其参数值分布见表1。其余参数，包括块、头部运动等模块的设置可由SimTB中文件“experiment_params_aod.m”获得。fMRI实测数据来自TReNDS实验室的公开数据，可从http:// trendscenter.org/trends/software/gift/Index.html网页获得，该数据是通过让被试者观察一个棋盘图案时所获得的fMRI数据，其参数设置见表2。

图2 fMRI数据的脑区模拟图

表1 构造脑区空间差异性的参数值

表2 实测fMRI数据集的参数设置

4.2 实验设置

实验中将本文算法h-SOBI和传统ICA算法和f-SOBI算法进行了比较，具体设置如下：

(1) fastICA，采用GIFT软件中的fastICA算法对仿真数据和实测数据进行信号分离，该软件下载地址为http://mialab.mrn.org/software/gift/index.html。将SimTB产生的仿真数据和实测数据分别输入GIFT中，然后选取FastICA 算法对数据进行处理。其中，仿真数据和实测数据的脑区独立分量个数分别为8和16。

(2) f-SOBI，相关函数中取值为4，其余参数采用文献[3]的设置，将该算法嵌入GIFT软件中，对SimTb产生的数据进行处理，分别获取8个激活脑区的时间、空间分布图。

(3) h-SOBI，相关函数中取值为4，其余步骤可参见表1，将该算法嵌入GIFT[12]软件中，对SimTb产生的数据进行处理，分别获取8个激活脑区的时间、空间分布图。

4.3 结果分析

4.3.1 仿真数据

本小节给出了仿真数据的分离结果，为了直观地观测空间图像分离的效果，图3分别显示了在阈值为1.5的情况下，ICA算法、f-SOBI算法以及h-SOBI算法对fMRI数据进行分离后获得的脑区图像。该图像分别选取第1个、第13个、第16个、第20个脑区，图中白色亮点及其周围黑色区域为激活脑区。

图3 3种算法提取的与任务有关的脑区图

从图3中可以看出，fastICA算法获得的激活区大小是3种算法中最大的，f-SOBI算法获得的激活区大小次之，而h-SOBI算法获得的激活区大小则是最小的，说明fastICA算法在3种算法中分离效果最好，能清楚地观察到分离的脑激活区，而h-SOBI相比其他2种算法，其分离效果较差，激活区不够明显。从图3中还可以看到，脑激活区域最亮的是fastICA算法获得的脑区，其次是f-SOBI，而h-SOBI算法获得的脑区较暗，表明fastICA分离信号的强度要高于其他2种算法。但是，3种算法所得到的激活脑区的位置是一致的，表明3种算法均能实现激活区的定位。

为了定量的分析3种算法的fMRI信号分离性能，本实验使用脑区定位的相对误差(brain position relative error, BPRE)作为评判准则，主要是计算差异性极显著的混合前与分离后脑激活区幅值最大点所对应的位置点的相对误差，即

图4给出了fastICA算法、f-SOBI算法以及h-SOBI算法分离fMRI信号的相对误差，从中可以看出，fastICA算法和f-SOBI算法的脑区定位误差均低于10%。h-SOBI算法除第5脑区的定位误差为15%，其余脑区的误差均低于10%，与其他2种算法的误差较为接近。

图4 3种算法的分离性能

本文实验通过运行时间来评判3种算法的计算复杂度。由于对算法计算复杂度影响较大是其解混矩阵的获取，因此表3给出了fastICA算法、f-SOBI算法和h-SOBI算法获取解混矩阵的运行时间，3种算法均在统一的MatLab平台下进行。

由表3可以看出，f-SOBI和h-SOBI算法获取解混矩阵的运行时间要小于fastICA,仅是fastICA算法的25%，其中，h-SOBI算法的运行时间更短，仅是f-SOBI算法的50%，因此，本文的h-SOBI算法的计算复杂度最低，fastICA算法的计算复杂度最高。

4.3.2 实测数据

本小节给出了实测数据的脑区信号分离结果，根据文献[13]可知，通过分离该真实数据可估计得到16个脑区分量，其中与视觉任务最为相关的2个脑区域分别是左视觉皮层和右视觉皮层，分别用蓝色和红色表示，如图5所示。

表3 3种算法分离仿真数据的运行时间(s)

图5 3种算法分离实测fMRI信号的脑区结果图

图5给出了fastICA算法、f-SOBI算法和h-SOBI算法分离实测fMRI数据得到的与任务相关度高的2个脑区分量切片图，且给出了与之对应的时间进程曲线图。将图5中3种算法分离得到的脑切片图进行对比可以看出，f-SOBI算法和h-SOBI算法分离得到的脑激活空间可以与fastICA算法分离得到的脑激活空间一一对应。在相同的阈值(1.0)下，h-SOBI算法显示的脑激活空间范围要小于f-SOBI算法和fastICA算法显示的脑激活空间图范围，其中h-SOBI显示的脑激活空间图范围更小。实验结果表明，对于实测数据，f-SOBI算法和h-SOBI算法的分离性能与fastICA算法的分离性能相差不大。

表4为3种算法分离实测数据的运行时间，由长到短依次为fastICA，f-SOBI和h-SOBI，分别是4.025 s，1.639 s以及0.885 s，表明f-SOBI和h-SOBI的运行时间要远小于fastICA，约为fastICA的50%，而h-SOBI的运行时间更短，约为f-SOBI的50%，与表3中的仿真数据结果基本一致。

表4 3种算法分离实测数据的运行时间(s)

5 结 论

针对传统fMRI脑区分离算法ICA计算复杂度高的问题，本文提出了一种基于哈达玛变换矩阵的二阶盲分离算法h-SOBI，通过该算法分离fMRI数据来定位脑激活区。该方法将稀疏的脑信号变换为非稀疏信号，然后根据信号的自相关矩阵来实现脑区信号的分离，使算法的计算复杂度大大降低，而脑区的定位误差与传统方法较为接近。在仿真实验中，本文分别对SimTB工具产生的fMRI仿真数据和TReNDS实验室公开的实测数据进行了测试。对于模拟的fMRI数据，本文算法的分离误差比fastICA算法高出4%，而运行时间却分别只有fastICA算法和f-SOBI算法的25%和50%。对于真实的fMRI数据，h-SOBI算法分离的脑激活空间能够与fastICA算法分离的脑激活空间一一对应，但是激活空间范围相比于fastICA更小。在运行时间上，f-SOBI和h-SOBI的运行时间分别约为fastICA的40%和20%。

[1] 唐焕文, 潘丽丽, 唐一源. SPM的数学基础及其在脑功能成像研究中的应用[J]. 应用基础与工程科学学报, 2005, 13(3): 6-14.TANG H W, PAN L L, TANG Y Y. The mathematical foundation of SPM and its application in brain functional imaging[J]. Journal of Applied Basic Science and Engineering, 2005, 13(3): 6-14 (in Chinese).

[2] CALHOUN V D, ADALI T, HANSEN L K. ICA of function MRI data: an overview[J]. Avsh-Alom Elyada, 2003, 33(5): 281-288.

[3] 程明. 独立成分分析算法应用于功能磁共振成像数据中[D]. 长春:吉林大学, 2013. CHENG M. Application of independent component analysis algorithm to functional magnetic resonance imaging data[D]. Changchun:Jilin University, 2013 (in Chinese).

[4] BELOUCHRANI A, ABED-MERAIM K, CARDOSO J-F. A blind source separation technique using second-order statistics[J]. IEEE Transactions on Signal Processing, 1997, 45(2): 434-444.

[5] NUZILLARD D, NUZILLARD J-M. Second-order blind source separation in the Fourier space of data[J]. Signal Processing, 2003, 83(3): 627-631.

[6] ALLEN E A, ERHARD E B, Yonghua WEI Y H, et al. A simulation toolbox for fMRI data: SimTB[EB/OL]. (2011-03-29) [2020-03-10]. http://mialab.mrn.org.

[7] COMON P. General linear model (GLM) applied to fMRI data analysis[J]. IEEE Transactions on Signal Processing, 2004, 36(2): 287-314.

[8] 彭尧, 熊馨. 一种改进的FastICA算法及其在fMRI数据中的仿真应用[J]. 软件导刊, 2018, 17(4): 67-70. PENG Y, XIONG X. An improved FastICA algorithm and its simulation application in fMRI data[J]. Software Guide, 2018, 17(4): 67-70 (in Chinese).

[9] CALHOUN V D, ADALI T, PEARISON G D, et al. A method for making group inferences from functional MRI data using independent component analysis[J]. Human Brain Mapping, 2001, 14(3): 140-151.

[10] HU W W, XU G Z. DOA estimation with double L-shaped array based on Hadamard product and joint diagonalization in the presence of sensor gain-phase errors[J]. Multidimensional Systems and Signal Processing, 2019, 30: 465-491.

[11] NUZILLARD D. Adaptation de SOBI à des données fréquentielles[EB/OL]. [2020-01-19]. http://documents. irevues.inist.fr/handle/2042/13128.

[12] The GIFT Documentation Team. Group ICA/IVA of fMRI toolbox (GIFT) manual[EB/OL]. [2020-01-15]. http://mialab.mrn.org.

[13] ERHARDT E B, RACHAKONDA S, BEDRICK E J, et al. Comparison of multi‐subject ICA methods for analysis of fMRI data[J]. Human brain mapping, 2011, 32(12): 2075-2095.

A blind separation algorithm with low complexity for fMRI brain activation

CHEN An-ying, WU Hai-feng, LI Dong

(School of Electrical and Information, Yunnan Minzu University, Kunming Yunnan 650500, China)

Functional magnetic resonance imaging (FMRI) is a medical imaging technology widely employed in brain region positioning for its non-invasiveness and high spatiotemporal resolution. However, the traditional FMRI signal separation algorithm was too complex and time-consuming to effectively apply the FMRI technology to brain function research. Aiming at the computational complexity of traditional FMRI brain separation algorithms, a blind separation algorithm was proposed based on the second-order Hadamard transform. This algorithm first calculated the correlation function of the blood oxygen level dependent (BOLD) signal in the fMRI data, and then performed eigenvalue decomposition to obtain the unmixing matrix, thereby realizing the activation of brain regions. Given the composition of the Hadamard being only 1 or-1, the complexity can be reduced for the BOLD signal correlation matrix calculation. The simulation results show that compared with the independent component analysis (ICA) of high-order statistics and the Fourier transform blind separation algorithm of second-order statistics, the calculation time of this algorithm was only 25% and 50% of theirs, respectively, while the positioning error was close.

functional magnetic resonance imaging; blind separation; independent components analysis; second order blind identifiability; brain activation area

TN 911.73

10.11996/JG.j.2095-302X.2020060947

A

2095-302X(2020)06-0947-07

2020-05-09；

2020-07-16

9 May，2020；

16 July，2020

国家自然科学基金项目(61762093)；云南省应用基础研究重点项目(2018FA036)；云南省高校智能传感网络及信息系统科技创新团队；2018年云南民族大学研究生创新基金项目(2018YJCXS176)

National Natural Science Foundation of China (61762093); Yunnan Provincial Applied Fundamental Research Key Project (2018FA036); Yunnan University Intelligent Sensor Network and Information System Technology Innovation Team; 2018 Yunnan Nationalities University Graduate Innovation Fund Project (2018YJCXS176)

陈安莹(1994-)，女，河南信阳人，硕士研究生。主要研究方向为fMRI信号处理。E-mail：857978569@qq.com

CHEN An-ying (1994-), female, master student. Her main research interest covers fMRI signal processing. E-mail：857978569@qq.com

吴海锋(1977-)，男，云南昆明人，教授，博士。主要研究方向为信号处理、机器学习和RFID。E-mail：whf5469@gmail.com

WU Hai-feng (1977-), male, professor, Ph.D. His main research interest cover signal processing, machine learning and RFID. E-mail：whf5469@gmail.com