基于超混沌系统的明文关联图像加密算法
芮 杰,杭后俊
基于超混沌系统的明文关联图像加密算法
芮 杰,杭后俊
(安徽师范大学计算机与信息学院,安徽 芜湖 241000)
随着计算机网络与多媒体技术的快速发展,数字图像传输的安全性问题显得越发突出。为此,提出了一种基于超混沌的明文关联图像加密算法,利用动力学更为复杂的超混沌系统作为混沌序列发生器扩大了密钥空间,采用扩散–置乱–扩散的加密框架对图像进行3阶段处理。其中深度扩散使用了更少的迭代次数,提高了效率,置乱算法通过扰乱图像中像素点的位置实现消除原图像中相邻像素点间的相关性。实验对密钥空间大小、算法效率、防明文攻击能力进行了分析和对比,仿真结果表明,该算法不仅具有更大的密钥空间,较高的运行效率,而且明文敏感性强,能够有效抵抗差分攻击,有很大的安全通信应用潜力。
图像加密;超混沌系统;明文关联;置乱;扩散
随着计算机网络与多媒体技术的快速发展,一方面数字图像因其具有形象生动、信息丰富、易于理解的先天优势而被人们大规模的应用,另一方面也出现了数字图像信息在没有得到所有者许可的情况下被非法复制、盗用,甚至篡改等行为,因此数字图像传输的安全性问题就越发突出。如何确保数字图像的传输安全也受到人们的普遍关注,而对图像进行加密是保证图像在网络中进行安全传输的重要技术。
混沌系统具有不确定性、不可预测性、初始值敏感等特点,一直是研究人员关注的热点。近年来,许多学者对基于混沌系统的图像加密技术进行了较为深入的研究,也得到了一些有效的加密方案。如FRIDRICH[1]率先提出了一种具有开创性的置乱–扩散加密体系结构。而低维混沌系统因其具有结构简单、易于实现的特点,被广泛地应用于混沌图像加密中[2-4]。但是低维混沌系统动力学特性简单且密钥空间小,无法抵御相空间重构,很容易被破译,安全性不高[5]。文献[6]和文献[7]先后提出了基于超混沌系统的图像加密方案,虽然增加密钥空间,但同时也增加了系统复杂度,效率低下。文献[8]提出了一种明文关联的图像加密算法,使得原图与混沌序列进行多轮的置乱扩散操作,提高了明文敏感性,但是需要进行多次迭代。文献[9-12]提出的算法虽然与明文关联,但是加密速度都比较慢,实际应用价值不高。文献[13]提出了一种多图像加密方案,但是图像之间没有关联,而且加密效率低,不能抵抗明文攻击。基于位级别的加密算法[14-17]通过对像素值进行位操作,使得置乱与扩散同时进行,虽然提高了效率,但抵御明文攻击能力比较弱。
针对上述问题,本文提出了一种基于超混沌系统的明文关联图像加密算法。主要在3个方面进行了改进:①深度扩散采取了更少次数的迭代,提高了加密效率;②利用动力学更为复杂的超混沌系统作为混沌序列发生器,扩大了密钥空间;③加密算法所用参数与明文图像相关,有效提高了抗明文攻击能力。
1 超混沌密码发生器
1.1 超混沌Lorenz系统
混沌系统因其鲜明的非线性动力学特征、初始值敏感性的特点,广泛应用于数字图像加密。与一般混沌系统相比,超混沌系统具有2个正的Lyapunov (李雅普诺夫特征)指数,其演化轨道的伸展与折叠特性比常规混沌系统更复杂,能够同时产生多组不同的伪随机序列,加密更加灵活,安全性更高。具体为
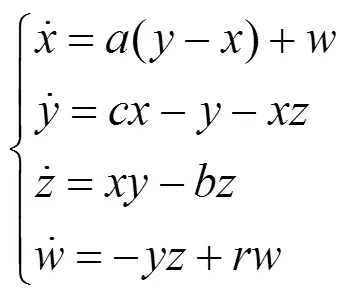
其中,,,和为超混沌系统Lorenz的参数,当=10,=8/3,=28,–1.52<≤–0.06时,系统处于超混沌状态;当=–1时,系统具有4个Lyapunov指数,1=0.3318,2=0.1586,3=0和4=–15.1752。系统状态初始值0,0,0和0的取值范围依次为:0∈(–40, 40),0∈(–40, 40),0∈(1, 81)和0∈(–250, 250)。
1.2 密码发生器
本文算法是采用扩散–置乱–扩散的加密框架,首先需要借助超混沌Lorenz系统产生6个伪随机矩阵,,,,,,分别用于扩散和置乱过程中。其中,矩阵,分别用于明文图像和中间密文的扩散过程,矩阵,,,分别用于中间密文图像的置乱过程。输入明文图像的大小均为×,令=max(,),1,2为2个8位伪随机数,具体步骤如下:
(1) 使用密钥中的{0,0,0,0}作为超混沌系统的初始值,迭代混沌Lorenz系统1+2次跳过超混沌系统的过渡态,再继续迭代×次得到4个混沌序列,记为{x},{y},{z},{w},=1,2,···,。
(2) 然后借助下列公式将混沌序列依次生成矩阵,,,,,。

2 加解密算法
本文利用更为复杂的超混沌系统作为混沌序列发生器,扩大了密钥空间,采取一种深度扩散方法,减少了扩散操作的迭代次数并提高了效率,进行明文相关的置乱操作,增强了明文敏感性。
2.1 第一阶段的扩散算法
借助随机矩阵将明文图像变换为,步骤如下:
步骤1.令=1,=1。将(,)变换为(,),即
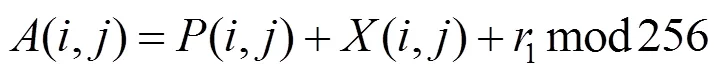
步骤2.令=+1。将(,)变换为(,),即
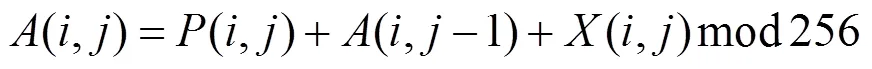
步骤3.如果<,跳转到步骤2;否则,令=1,=+1,如果<,跳转到步骤4;否则,跳转到步骤6。
步骤4.将(,)变换为(,),即

步骤5.跳转到步骤2。
步骤6. 结束。
2.2 明文关联的置乱算法
置乱算法通过扰乱图像中的像素点位置消除原图像中相邻像素点的相关性,本文明文关联的置乱算法是将图像置乱为图像,步骤如下:
步骤1.将图像中给定的一个像素点坐标(,),根据下式计算得到(,)的值。
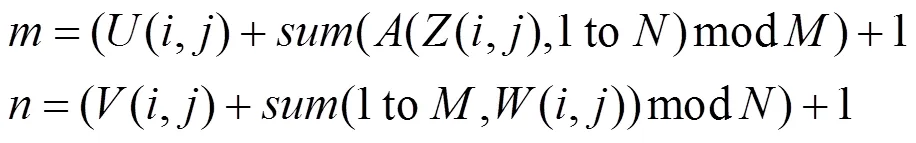
如果=或(,),或者=或(,),或者(,)=,或者(,)=,则(,)位置保持不变;否则,(,)与(,)互换位置。
步骤2.当坐标(,)按从左到右、从上到下的扫描顺序遍历图像中的所有像素点时,重复步骤1,将图像转化为图像。
2.3 第二阶段的扩散算法
与第一阶段的扩散算法不同之处在于,明文无关的扩散算法2是从图像的最后一个像素点向前扩散,其借助于伪随机矩阵将图像变换成矩阵,步骤如下:
步骤1.令=,=将(,)变换为(,),即
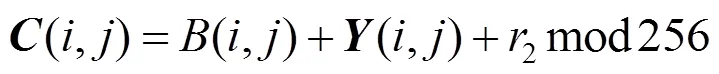
步骤2.令=–1。将(,)变换为(,),即
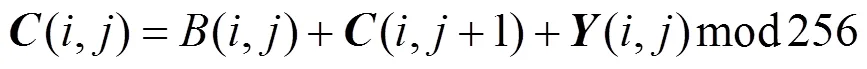
步骤3.如果>1,跳转到步骤2。否则,=,=–1如果≥1,跳转到步骤4;否则,跳转到步骤6。
步骤4.将(,)变换为(,),即
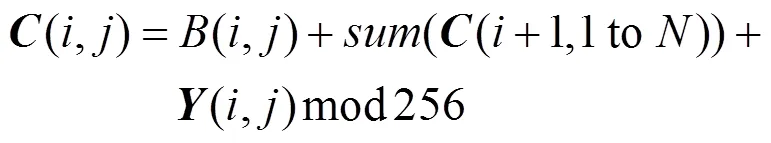
步骤5.跳转到步骤2。
步骤6.结束。
矩阵即为得到的密文图像。
2.4 解密算法
解密过程是加密过程的逆过程,具体过程如下:
步骤1.输入密文图像以及6个伪随机矩阵。
步骤2. 执行第二阶段扩散算法的逆算法。
步骤3.执行中间置乱算法的逆算法。
步骤4.执行第一阶段扩散算法的逆算法。
步骤5.输出明文图像。
3 实验结果与安全性分析
实验使用的计算机配置为2.60 GHz处理器,8 G内存,Windows 7操作系统,仿真软件为MATLAB R2017a。采用的超混沌系统参数为=10,=8/3,=28,=–1,超混沌系统初始值为0∈(–40, 40),0∈(–40, 40),0∈(1, 81)和0∈(–250, 250)。
不失一般性,本文选用大小为256×256的lena,pepper以及512×512的lena等多幅灰度图像作为测试图像(图1)。

图1 实验测试用例
3.1 密钥空间分析
密钥空间是衡量密码系统安全性的一个重要指标。密钥空间越大,抵抗穷举能力越强,加密系统安全性越高。在本文加密算法中,密钥为={0,0,0,0,1,r},其中,0∈(–40, 40),0∈(–40, 40),0∈(1, 81),0∈(–250, 250),0,0,0的步长为10–13,0的步长为10–12,1和2步进为1,因此密钥空间大小约为1.6777×1064,远远超过安全密钥空间2100的限制条件,可以很好地抵抗密钥攻击。
取初始密钥为[3.3133 12.0546 40.8879 –34.5677 35 201],对256×256的pepper图像加解密效果如图2所示。

3.2 差分攻击安全性分析
差分攻击是指使用同一密钥借助图像加密系统对微小差别的2个明文图像进行加密,比较2个密文图像的差别来达到破解的目的。如果2个密文图像的差别迥异,则称该图像密码系统具有良好的明文敏感性。通常使用像素改变率(number of pixels change rate,NPCR)与归一化改变强度(unified average changing intensity,UACI)作为衡量指标。UACI理论值是33.4635%,NPCR的理论值是99.6094%。现以256×256的lena,pepper图像为例,改变其中任意一个像素,计算密文图像的NPCR和UACI值,本文对图像像素点是随机选取的,像素值的变化量为1,为了加强实验结果的说服性,重复实验100次,根据式(10)和式(11)计算得到UACI和NPCR的值,最后,取其平均值作为最终实验结果记录见表1和表2。可以看出,本文算法的UACI和NPCR的值更接近理论值,有更好的明文敏感性,抗明文攻击能力更强。
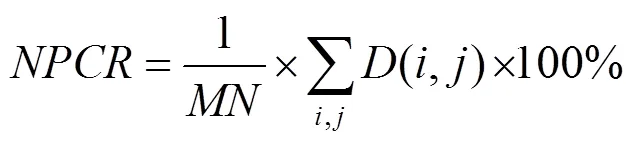
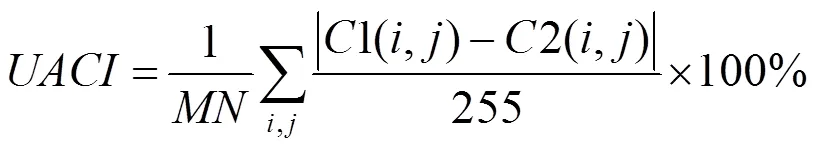
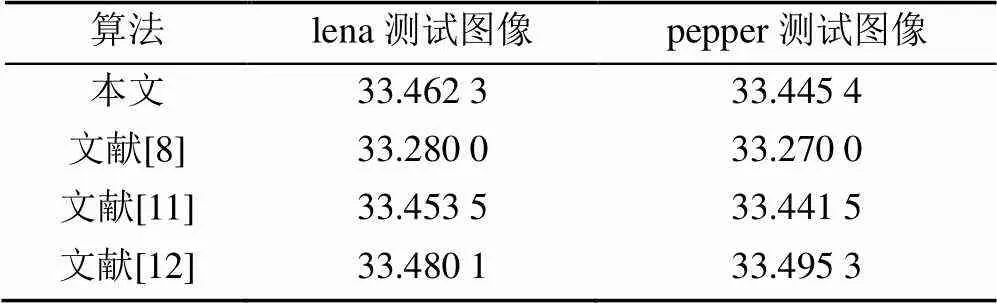
表1 不同加密算法UACI值(%)
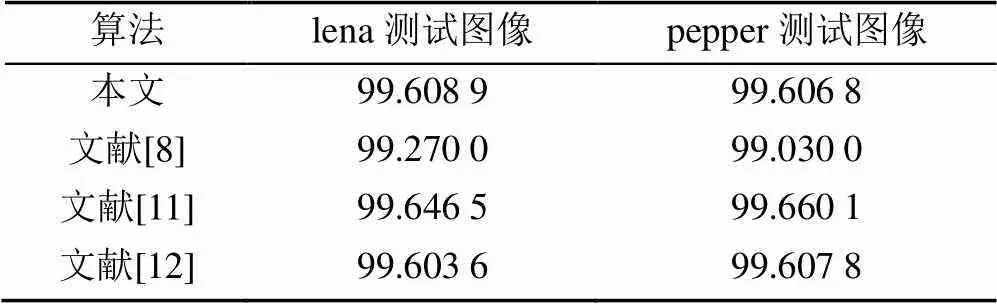
表2 不同加密算法NPCR值(%)
3.3 密钥敏感性分析
密钥敏感性分析是指当密钥发生微小变化时,加密同一明文图像得到的2个密文图像的差别情况。例如将原始密钥中0=3.3133,修改为0= 3.3133×10–13,而其他密钥保持不变,采用新旧密钥加密同一lena图像,图3(a)和(b)分别为利用原始密钥和新密钥加密得到的2幅密文图像,图3(c)为2幅密文图像的差图像。

图3 密钥敏感性测试
从测试结果可以看出,2幅密文图像的差图像呈噪声形式,直观上反映2个密文差异显著,攻击者试图通过差值图像进行破解几乎是不可能的,表明本文加密算法具有很强的密钥敏感性。
3.4 加密效率测试
密码学专家普遍认为,一个具有极高安全性的密码系统是容易设计的,但是,一个加密速度快且安全性高的密码系统才具有实用和研究价值。本文所提算法在利用混沌系统生成密码矩阵阶段,还有图像置乱和扩散过程,采用了加法取模等多种运算相结合,满足优良密码系统复杂度高的特点。为了更好地验证本文算法具有更高的实用价值,采用2幅大小分别为256×256和512×512的lena灰度图像进行多次加密时间测试,然后取加密时间的平均值作为结果,表3给出了本文算法与其他相关文献所给算法的对比。可以看出,本文算法具有更高的执行效率。
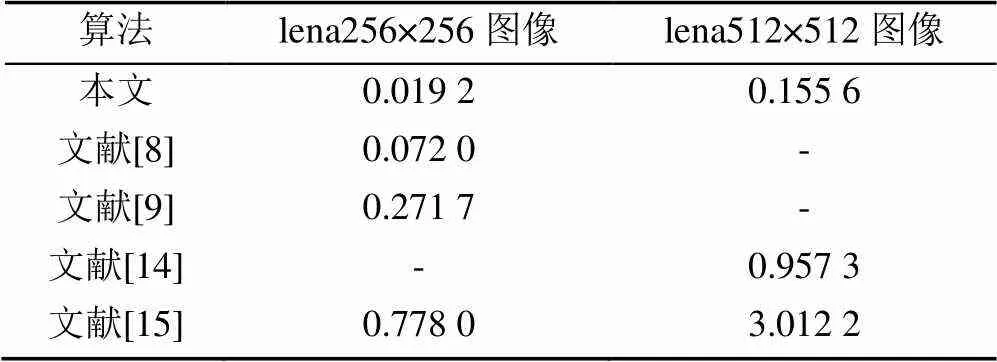
表3 不同加密算法的运行时间比较(s)
4 结束语
本文利用动力学更为复杂的超混沌系统提出了一种明文关联图像加密算法,采用一种改进的“扩散-置乱-扩散”加密框架,其中2个阶段的深度扩散均采用较少的迭代次数。本文算法不仅保留了低维混沌系统效率高、形式简单和高维混沌系统大密钥空间的特点,同时由于加密的过程不仅与密钥有关,也与明文相关,即拥有相同的密钥但不同的明文图像对应着不同的密码,具有很强的明文敏感性,增强了算法抵御差分攻击的能力。围绕密钥空间及安全性、算法效率、防明文攻击能力等方面与主流算法做了对比分析,从而验证了本算法的有效性和实用性。
[1] FRIDRICH J. Symmetric ciphers based on two- dimensional chaotic maps[J]. International Journal of Bifurcation and Chaos, 1998, 8(6): 1259-1284.
[2] LIU L F, MIAO S X. A new image encryption algorithm based on logistic chaotic map with varying parameter[J]. Springerlus, 2016, 5: 289.
[3] HUA ZY, ZHOU YC. Image encryption using 2D logistic-adjusted-sine map[J]. Information Sciences, 2016, 30: 237-253.
[4] YU J, LI Y, XIE X, et al. Image encryption algorithm by using the logistic map and discrete fractional angular transform[J]. Optica Applicata, 2017, 47(1): 141-155.
[5] ZHANG Y Q, WANG X Y. A symmetric image encryption algorithm based on mixed linear–nonlinear coupled map lattice[J]. Information Sciences, 2014, 273: 329-351.
[6] 刘云, 郑永爱, 莫丽丽. 基于超混沌系统的图像加密方案[J]. 中南大学学报: 自然科学版, 2009, 40(S1): 121-126. LIU Y, ZHENG Y A, MO L L. Image encryption scheme based on hyperchaos system[J]. Journal of Central South University: Science and Technology, 2009, 40(S1): 121-126 (in Chinese).
[7] 卢辉斌, 孙艳. 基于新的超混沌系统的图像加密方案[J]. 计算机科学, 2011, 38(6): 149-152. LU H B, SUN Y. Image encryption scheme based on novel hyper-chaotic System[J]. Computer Science, 2011, 38(6): 149-152 (in Chinese).
[8] WANG X Y, WANG Q, ZHSANG Y Q. A fast image algorithm based on rows and columns switch[J]. Nonlinear Dynamics, 2015, 79(2): 1141-1149.
[9] RAJ R, SINGH P K, SINGH R S. Multi-image encryption using genetic computation[J]. CSI Transactions on ICT, 2016, 4(2-4): 1-7.
[10] 吕翔, 王晓洁, 杨刘洋, 等. 一种抗差分攻击的图像加密算法[J]. 浙江师范大学学报: 自然科学版, 2020, 43(1): 39-45. LU X, WANG X J, YANG L Y, et al. An image encryption algorithm against differential attack[J]. Journal of Zhejiang Normal University: Natural Sciences, 2020, 43(1): 39-45 (in Chinese).
[11] NIYAT A Y, MOATTAR M H, TORSHIZ M N. Color image encryption based on hybrid hyper-chaotic system and cellular automata[J]. Optics & Lasers in Engineering, 2017, 90: 225-237.
[12] WU J H, LIAO X F, YANG B, Image encryption using 2D Hénon-Sine map and DNA approach[J]. Signal Processing, 2018, 153: 11-23.
[13] 谢国波, 高兆曦. 明文关联的多混沌彩色图像加密算法[J]. 计算机工程与设计, 2019, 40(4): 920-930. XIE G B, GAO Z X. Plaintext related color image encryption algorithm based on multiple chaotic maps[J]. Computer Engineering and Design, 2019, 40(4): 920-930 (in Chinese).
[14] SHAFIQUE A, SHAHID J. Novel image encryption cryptosystem based on binary bit planes extraction and multiple chaotic maps[J]. THE European Physical Journal Plus, 2018, 133(8): 331.
[15] CHAI X L. An image encryption algorithm based on bit level Brownian motion and new chaotic systems[J]. Multimedia Tools and Applications, 2017, 76: 1159-1175.
[16] YE G D, PAN C, HUANG X L, et al. An efficient pixel-level chaotic image encryption algorithm[J]. Nonlinear Dynamics, 2018, 94: 745-756.
[17] 朱淑芹, 王文宏, 李俊青. 对像素置乱和比特替换混沌图像算法的破解[J]. 计算机应用, 2017, 37(Z2): 44-47. ZHU S Q, WANG W H, LI J Q. Breaking a chaotic image encryption algorithm based on pixel scrambling and bit substitution[J]. Journal of Computer Applications, 2017, 37(Z2): 44-47 (in Chinese).
Plaintext correlation image encryption algorithm based on hyper-chaotic system
RUI Jie, HANG Hou-jun
(School of Computer and Information, Anhui Normal University, Wuhu Anhui 241000, China)
With the rapid development of computer networks and multimedia technologies, the security problem of digital image transmission has become increasingly salient. A hyper-chaotic encryption algorithm was proposed for plaintext associated images. The algorithm employed hyper-chaotic systems with more complex dynamics as a chaotic sequence generator, expanded the key space, and utilized a diffusion-scrambling-diffusion encryption framework. The method performed three-stage processing on the image, of which the depth diffusion improved efficiency using fewer iterations. The scrambling algorithm eliminated the correlation between adjacent pixels in the original image by disturbing the pixel positions. The experiment analyzed and compared the key space size, algorithm efficiency, and anti-plaintext attack capability. The simulation results show that the algorithm has not only larger key space and higher operating efficiency, but also strong plaintext sensitivity, thus effectively resisting differential attacks with great potential for secure communication applications.
image encryption; hyper-chaotic system; plaintextcorrelation; scrambling; diffusion
TP 309.7
10.11996/JG.j.2095-302X.2020060917
A
2095-302X(2020)06-0917-05
2020-06-10;
2020-08-03
10 June,2020;
3 August,2020
安徽省高等学校自然科学研究重点项目(KJ2017A326)
The Provincial Natural Science Research Project of Anhui Colleges (KJ2017A326)
芮 杰(1996-),男,安徽马鞍山人,硕士研究生。主要研究方向为数字图像处理。E-mail:1591487080@qq.com
RUI Jie (1996-), male, master student. His main research interest covers digital image processing. E-mail:1591487080@qq.com
杭后俊(1965-),男,安徽芜湖人,副教授,硕士,硕士生导师。主要研究方向为计算机图形学、计算机辅助几何设计、数字图像处理。 E-mail:hjhang@ahnu.edu.cn
HAUNG Hou-jun (1965-), male, associate professor, master. His main research interests cover computer graphics, CAGD, image processing. E-mail:hjhang@ahnu.edu.cn

