修正压力与表面张力计算的两相流自由界面运动模拟
朱晓临,周韵若,何红虹
修正压力与表面张力计算的两相流自由界面运动模拟
朱晓临,周韵若,何红虹
(合肥工业大学数学学院,安徽 合肥 230009)
在利用光滑粒子流体幼力学(SPH)方法进行多相流的模拟中,多相流在交界面处由于密度不连续、粒子界面的压力计算出现误差,出现界面处压力振荡,界面破碎的问题。针对上述问题,提出了新的压力梯度近似公式和改进的界面处人工斥力公式,使交界面更加清晰、光滑、无穿透、模拟效果更好。此外,通过给出基于密度权重的色函数计算公式,对大密度比多相流界面处的表面张力计算公式进行了改进,使得多相流交界面密度过渡更加光滑,模拟效果更好。最后,通过溃坝、Rayleigh-Taylor界面不稳定性,非Boussinesq锁定交换问题3个仿真实验,得到了不同时刻界面粒子分布图、界面锋面距离等。结果验证了新的压力梯度近似公式以及界面处人工斥力公式的合理性;通过空气中液滴形成仿真实验,得到了圆形液滴形成的粒子变化图,结果验证了该改进的表面张力计算方法的有效性。
SPH方法;多相流;压力梯度近似公式;人工斥力;色函数;表面张力
2005年,柳有权等[1]提出流动系统中存在多种不互溶的流体,称为混合流;而若相态多于一个,且各相态之间不互相渗透或发生化学反应,则称为多相流。近年来,多相流动的数值模拟技术是计算流体动力学(computational fluid dynamics,CFD)领域研究的热点和前沿课题之一。液液两相流动与气液两相流动在日常生活中十分普遍,如通过预先模拟实现药物在人体血管中的精确定位打靶技术以及气泡上升至自由表面最终破裂的现象。
而在两相流动数值模拟技术中,如何处理两相交界面处的界面稳定性是最近几年研究中的热点问题。
常见的界面不稳定性有2类:① 2种不同密度的流体在重力或惯性力的作用下的界面不稳定性问题,通常称之为Rayleigh-Talor界面不稳定性问题;② 2种流体之间有切向速度差,因此造成界面上的不稳定性,通常称之为Kelvin- Helomholtz不稳定性。
2003年,COLAGROSSI和LANDRINI[2]将1995年MONAGHAN和KOCHARYAN[3]提出的模拟小密度比两相流的方法应用于气液两相流模拟,发现交界面处出现剧烈的数值振荡。该方法使用弱可压缩模型建模,根据粒子的体积而不是密度进行建模,进行压力梯度计算,避免了气-水界面密度不连续的问题。此方法需要极小的时间步长作为支撑,整个模拟需要的时间较长。
2006年,HU和ADAMS[4]提出了可计算宏观和微观流场的光滑流体粒子动力学(smoothed particle hydrodynamics,SPH)方法,采用不同的粒子近似函数,即粒子近似函数是针对邻近点体积而不是密度,但其并未计算大密度比复杂界面流场。
2007年,HU和ADAMS[5]提出了一种不可压缩的多相SPH方法,主要通过一种新的多相投影公式来离散梯度与散度算子,但是该方法需要求解压力泊松方程,整个计算过程十分耗时。
2008年,SOLENTHALER和PAJAROLA[6]提出一种使用标准SPH模型去模拟大密度比两相流。其主要通过计算粒子数密度而不是计算粒子密度去保证两相界面密度的连续性,从而推出压力项与黏性项的计算公式。该方法简单,但仍存在局限性。其直接基于密度进行修正的方法有效解决了两相流密度上的不连续性,但是在计算压力项,尤其针对体积较小的流体时,两相流体间还是会存在较大的间隙,无法保证交界面的连续性。
2013年,MONAGHAN和RAFIEE[7]通过在交界面上引入斥力项维持界面的光滑与完整。该方法简单,但是对于声速的使用依旧是非物理的,同时将界面处粒子视为刚性边界粒子,对粒子的运动范围设置限制,其好处是稳定界面,但是却是不符合物理规律,理论上界面上的粒子可以向各个方向进行运动,模拟缺乏处理湍流的能力。
2015年,CHEN等[8]针对密度差较大的多相流,提出了自己的SPH模型,其舍弃了文献[4]提出的颗粒间压力的想法,通过将界面粒子的邻近粒子中非同相粒子看成同相粒子,其速度、体积、位置等信息与初始异相粒子相同。质量与密度使用当前相流体粒子的质量与密度;同时提出了一种新的针对大密度比的多相流密度初始化的方法,以及为避免初始负压强,在状态方程中加入初始压强项;但是该方法并未在界面处加入人工斥力项,界面较为粗糙。
2015年,LIND等[9]针对气-水界面的大密度比问题提出一种不可压缩-可压缩建模方法。将水相作为不可压缩相,空气相作为弱可压缩相进行建模,使得模拟中保证了界面处材料的不连续性以及压力和运动速度的连续性。但是该方法在求解水相的压力时,同样需要解费时的压力泊松方程,计算量较大。
2018年,KRIMI等[10]提出加入连续压力表面方程的SPH模型模拟界面多相流,主要加入一个压力表面系数,提高了界面处的稳定性与光滑性;但是该方法在模拟过程中,对于界面系数的选择较为困难,缺乏量化的标准去选择表面系数。
2019年,杨秋足等[11]提出了一种利用弱可压缩SPH方法来对大密度比多相流模拟建模的方法;主要在求解界面压力与密度处引入了黎曼解的相关思想,但是此方法计算复杂,耗时较长。
尽管经典的SPH方法成功地模拟了单相流体的流动,但由于多相流体的流动中多相物理条件的不同导致单相流体的SPH方法难以适用于多相流。主要的问题是两相流密度在界面处是跳跃的,但是SPH方法是一个平滑过渡的过程,每个粒子都有一个紧致的支持域,通过紧致的支持域内均匀分布的粒子计算出当前粒子的各项物理属性。当支持域与界面相交时,界面另一侧的密度会错误地影响局部密度和压力场的计算,从而影响有关粒子的加速度与速度的计算,导致粒子下一个时间步长的位置错误。因此,本文针对多相流界面处的密度、压力、表面张力等物理量进行单独处理,以保证密度梯度的连续和表面张力的连续,避免界面处的粒子在运动过程中出现振荡现象。
1 控制方程与SPH方法
1.1 控制方程
1977年,LUCY[12]首次提出SPH方法,之后被GINGOLD和MONAGHAN[13]用于模拟天体物理问题。1991年,LIBERSKY和PETSCHEK[14]将其扩展到流体模拟领域,促进了SPH对于水动力学的应用研究。
流体运动控制方程为



利用弱可压缩模型描述不可压缩流体,采用如下状态方程[8]

1.2 SPH方法
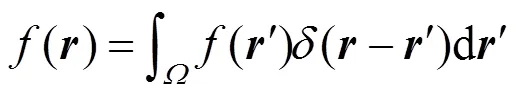
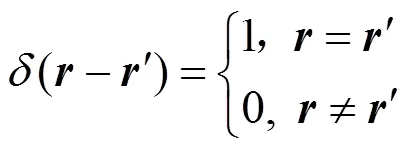
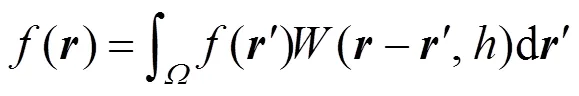
其中,为平滑核函数(smoothing kernel function),为核函数的支持域长度。

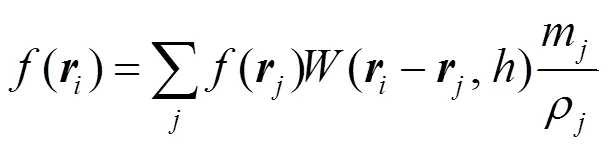
其中,为粒子的邻近粒子;m为粒子的质量;为粒子的密度。
分别对()进行梯度和拉普拉斯运算,即分别对其光滑核函数进行梯度和拉普拉斯运算
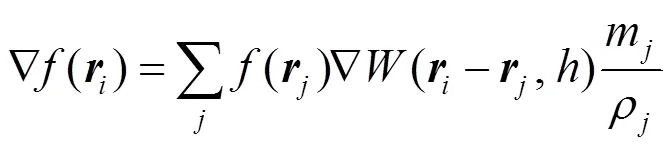
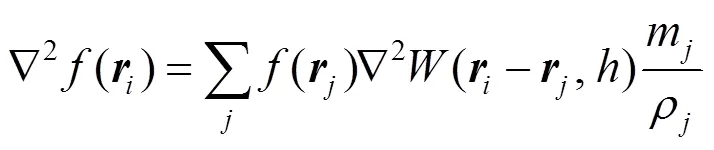
1.3 黏性项
考虑到流体具有黏性,动量方程中黏性项的形式为
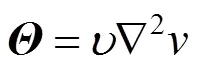
本文采取文献[16]提出的黏性项表达式,即

其中,=-;=-;=;ÑW=Ñ(-,)|=r。
当使用SPH方法进行流体运动的计算过程中,需要采用人工黏性项以避免激波附近出现非物理震荡。本文采用MONAGHAN和GINGOLD[17]提出的人工黏性项,即
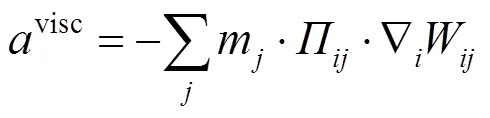

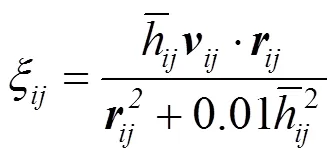
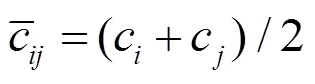
2 本文工作
2.1 新的粒子压力梯度近似公式
针对上述多相流界面处存在的问题,下面对多相流界面处的压力梯度近似公式进行改进,解决多相流数值模拟中界面不光滑的问题,并与文献[8]的结果进行对比。文献[4]提出的界面处的压力项为
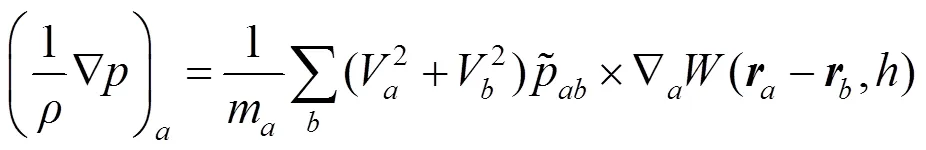
其中,粒子间压力项为

式(18)对于小密度比两相流成立,但是对于大密度比两相流,在界面处,p»p,<<,此时,式(18)变为

可以发现,加入的粒子间压力项主要是由密度较低的流体的压力引导。此时可以等价为只有小密度流体对大密度流体有作用,而大密度流体对小密度流体无作用,显然有问题。同时,在界面处,进行邻近粒子搜索时,混合着两相粒子,会对颗粒间压力项计算产生误差。
文献[8]对式(17)进行了改进,对界面处的压力梯度近似公式进行了修改,具体形式为
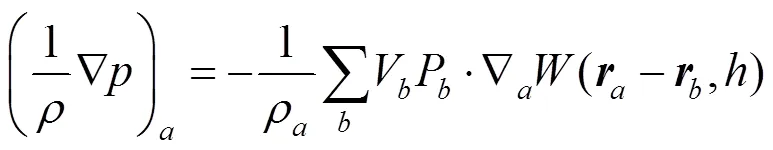
由式(20)可以发现,在计算界面处粒子间压力项时,使用的均为粒子b的相关信息。文献[8]所做的针对性处理是将粒子a的邻近粒子中的非同相粒子均人为地看作同相粒子,使用原有的粒子的信息(除了质量、密度),如图1所示。
上述做法需要在计算中人为地更改粒子的物理属性,增加了额外的计算量。
本文基于牛顿第三定律,作用力等于反作用力,在界面处大密度粒子与小密度粒子对彼此的作用力应是相等的,这样才可以保证界面的光滑与完整;否则,粒子会因为压力不等在界面处出现振荡,将式(20)改成对称形式,保证界面处压力的连续,得到新的粒子压力梯度近似式为
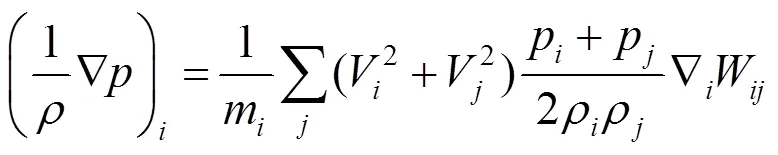
使用当前粒子与邻近粒子的物理信息,避免了人为修改粒子的物理信息,减小了计算量。对比式(17),式(21)解决了大密度粒子对小密度粒子无影响的问题,同时保证了界面处压力的连续性,其作为粒子压力梯度近似公式是合理的。
在压力场中


2.2 改进的人工斥力公式
在实验中,发现仍存在少量高密度粒子滞留在低密度粒子上方。本文提出了一种新的压力梯度近似公式,保证低密度粒子和高密度粒子受到的力大小相等,方向相反。但低密度粒子与高密度粒子依旧存在着质量上的不连续,即相互作用力产生的加速度偏差较大,导致出现上述的实验现象。为了与物理上相斥流体界面现象相对应(即相斥流体界面间存在明显的分层现象),故在界面处加入人工斥力,即


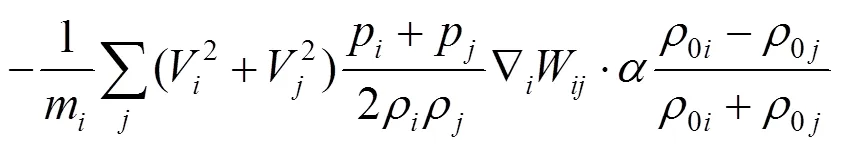
式(25)有效解决了不同相粒子在界面处出现混合的情况,保持了界面的光滑性。这与现实生活中2种密度不同,互不相溶的液体相互接触的情形相同。
2.3 改进的表面张力计算公式
2010年,ADAMI等[18]提出了多相流中的表面张力计算公式。
定义色函数如下
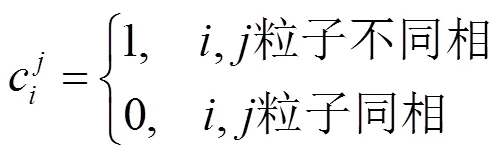
而在实验中发现,针对大密度比多相流,上述的色函数计算方式往往会在界面处出现颜色梯度的跳跃,导致界面出现毛糙等现象。本文给出基于密度权重的色函数计算公式
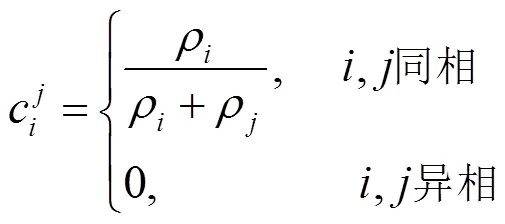
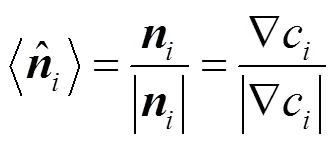

通过外法向可以计算两相流界面曲率,即

其中,为计算域的维度。将曲率和外法向代入表面张力公式,得到基于密度权重的色函数的改进的表面张力计算式为
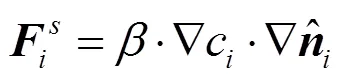
根据上述讨论,本文动量方程的离散形式为
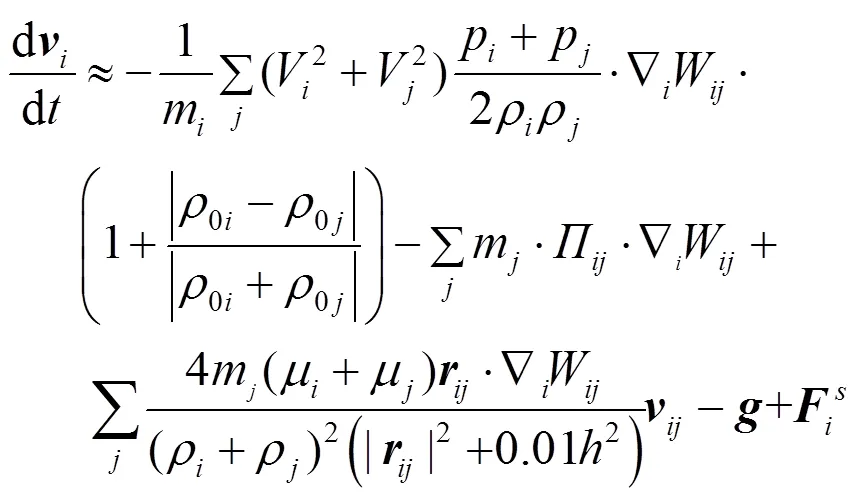
3 实验结果与分析
本节的前3个仿真实验,包括溃坝、R-T不稳定性、非Boussinesq交换,检验本文新的压力梯度近似公式和改进的界面处人工斥力公式的合理性;其中,算例1的密度比大于800,算例2和3的密度比小于2。第4个仿真实验——圆形液滴形成,验证本文改进的表面张力计算公式的有效性。
本文的实验在Windows 10系统上,开发环境为Visual Studio 2013与openGL,实验配置为Intel(R) Core(TM) i7-8570H,2.20 GHz CPU,8 G内存,NVIDIA Geforce GT 1060显卡。
3.1 溃坝(算例1)
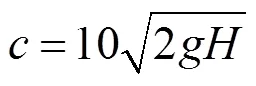

图2 二维溃坝模拟粒子效果图
从图2可以看出,受重力的作用,初始静止的水沿着左边的固壁边界向右加速运动(图2(a1)),水面的高度自左至右不断降低,水的速度不断增大,直至到达右边的固壁边界处,与右边的固壁边界发生撞击,速度减小但压力增大,水自由面沿墙竖直向上爬升(图2(a2))。与当水到达最高点且速度降为零时,重力又使水沿右边的固壁边界反向加速运动,上行与下行的水流在右边界1/4处汇集,形成了“鼓包”区域(图2(a3)),与图2(b4)相比,本文方法在鼓包形成区域形态更为完整,且液体没有明显的压力振荡。由于上部的水继续下落,受挤压的鼓包形成了“水射流”(图2(a4));“水射流”包裹部分空气,重力导致水射流向左下方下落,形成类似“水射流”冲击自由表面,撞击后再次形成“水射流”(图2(a5))。与图2(b4)、图2(b5)相比,本文的方法在界面处粒子无明显的“黏滞”状态且界面处无明显的压力振荡。

图3 三维溃坝模拟粒子效果图
图3为三维溃坝实验结果。实验结果表明,本文方法与文献[8]的方法结果进行对比,本文方法在溃坝计算中的气-水界面处更加光滑。在流体运动的过程中,虽然流体的压力连续变化,但是计算过程中液面并未出现明显的压力振荡。
图4给出了液面最高点随时间变化的趋势。从中可以看出,本文实验结果与文献[18]基本一致,说明本文方法在计算大密度比界面问题中的合理性。
3.2 Rayleigh-Taylor界面不稳定性(算例2)
采用多相流SPH方法,文献[5]、文献[7]和文献[8]均计算了R-T界面,其中文献[8]计算R-T界面的实验效果最好。
初始状态如图5(a)所示。当=0时,密度为1 750 kg/m3的流体(红色)置于密度1 000 kg/m3的流体(蓝色)上方,界面形状为=1.0-0.15(2p)。取0.05,D=0.003 s。
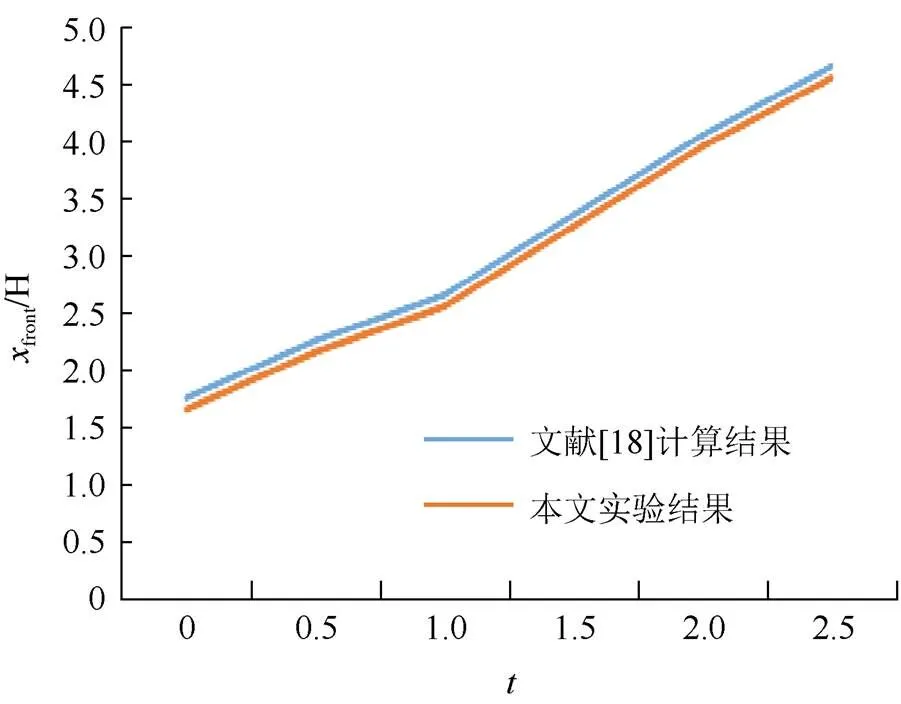
图4 水前端与时间的关系

图5 R-T实验本文方法的不同时刻粒子分布图
从本文的实验结果(图5)可以看出,本文算法清晰地捕捉到不同时刻2种流体界面,界面并未发现明显的压力振荡,高密度与低密度流体分别呈斜射入状进入对方区域。通过对最终效果的比较(图5(d)与图6),本文方法在界面处的光滑性更好,计算中未出现明显的粒子“集聚”现象,避免了形成虚假的压力场(即人工表面张力)导致界面曲率变大,界面之间出现狭小的空隙。

图6 文献[8]方法
定量验证计算结果,图7给出了低密度流体界面最高点位移随时间变化的曲线,从图6中可以看出,本文实验结果基本与LAWRIE 和DALZIEL[19]得到的Layzer理论值重合,同时与文献[8]的结果相比,在范围内,本文得到的-曲线与Layzer理论值更为符合。说明本文在处理大密度比界面问题中是合理的。

图7 低密度流体y-t曲线(算例2)
3.3 非Boussinesq锁定交换问题(算例3)
挡板隔开矩形水平管两侧不同密度的流体(图8),当瞬间抽去中间挡板(白色区域)时,2种流体发生相对运动,其密度比大的情况称之为非Boussinesq锁定交换问题,反之称为Boussinesq锁定交换问题。取矩形管道的长为1.28 m,宽为0.32 m,挡板左侧为低密度(红色)流体,右侧为高密度(蓝色)流体(图8),各变量见表1。

图8 初始界面示意图

表1 挡板左右两侧参数表
从图9可以看出,低密度流体与高密度流体分别沿水平管上、下壁面自右至左和自左至右运动,形成剪切界面。随着计算时间的增长,左右相对运动的界面存在着切向速度差,出现了Klelvin- Helmholtz界面不稳定性。本文通过使用对称形式的粒子间压力,使得界面两侧压力符合牛顿第二定律,保证了界面两侧压力的连续性,使得交界面更加光滑,同时在界面处对异相粒子施加人工应力,避免粒子在异相液体相中的滞留情况。实验结果表明(图9(a)和图9(b)),本文方法的效果更好,异相流体界面分层更加清晰。

图9 运动后界面效果图
图10给出轻重流体锋面与挡板距离/随时间变化的曲线。从中可以看出,曲线的变化趋势相同,二者近似呈线性变化,与文献[20]计算和实验结果相符合。其中对重流体,本文实验结果略低于计算结果值,初始误差较小,误差随增大而增大并趋于恒定。对于轻流体,本文实验结果与计算结果相比,初始时误差较大,随着计算时间不断增大,曲线逐渐趋于统一,误差趋近于0。说明本文方法在计算大密度比界面问题中是合理的。
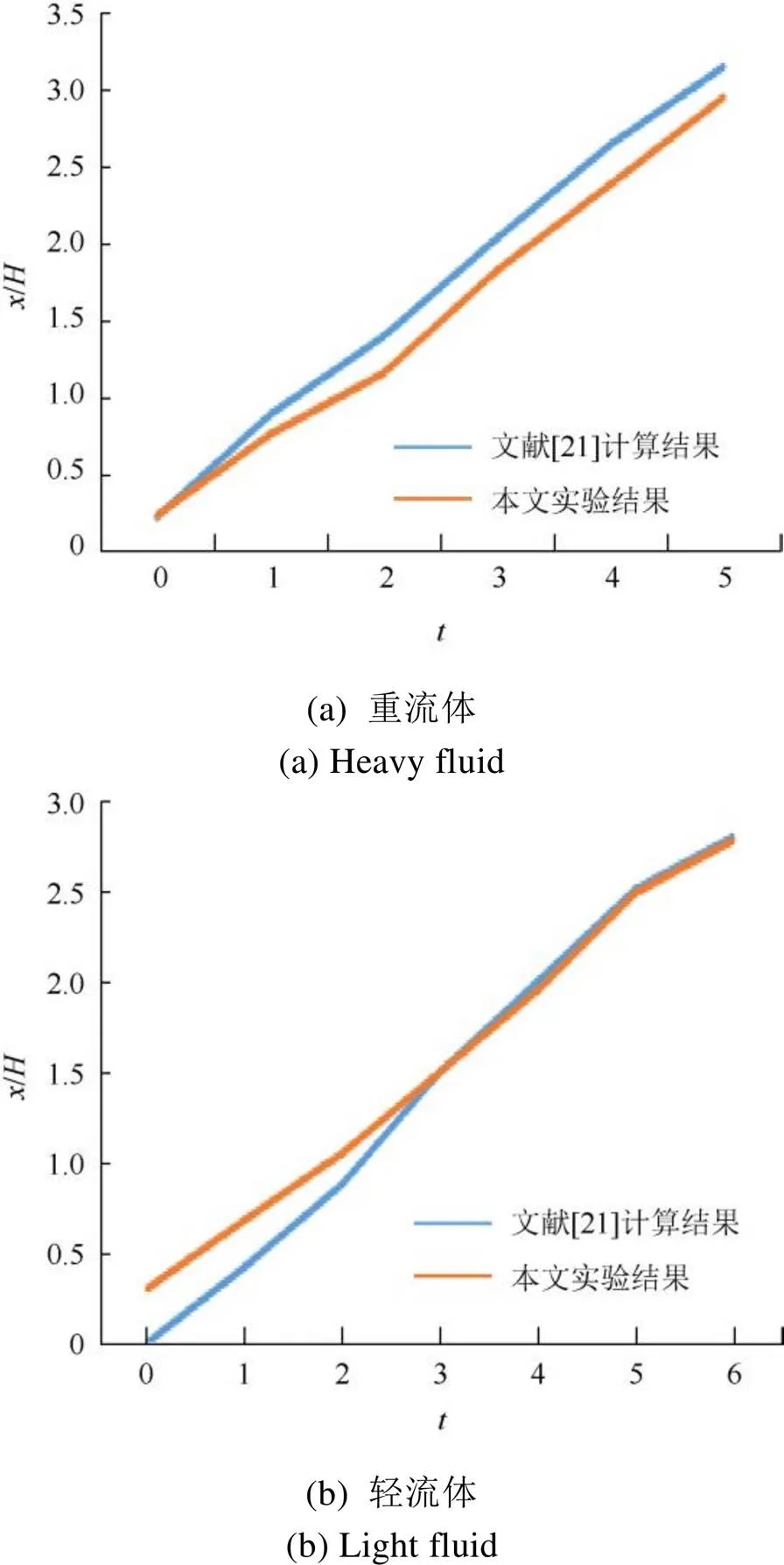
图10 轻重流体(x/H)-t曲线
3.4 空气中圆形液滴形成变化实验(算例4)
实验物质参数见表2。为验证多相流大密度比界面处的表面张力计算公式的有效性,本文进行含有表面张力的经典实验——圆形液滴形成变化仿真实验。初始形态如图11所示,其中,黄色粒子表示水粒子,紫色粒子为空气粒子。

表2 实验中的物质参数
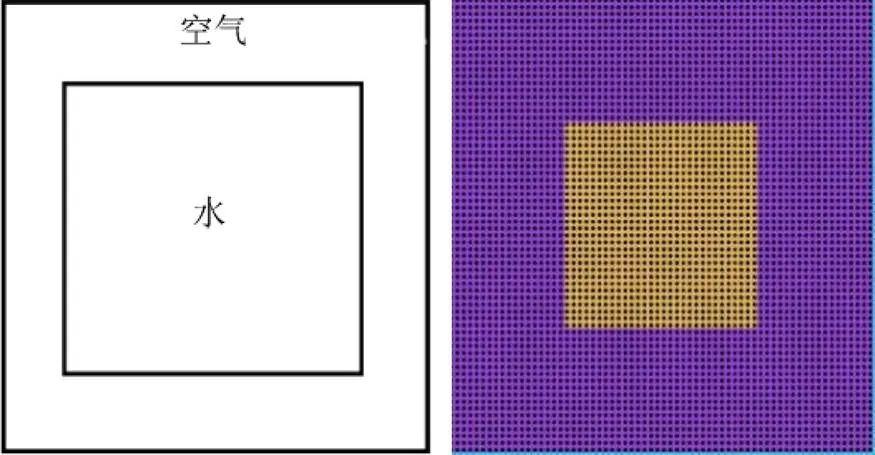
图11 空气中圆形液滴形成变化初始图
液滴在表面张力的作用下不断振荡,由于黏性使得动能不断耗散,最终稳定成圆形液滴,如图12所示。文献[21]是当前模拟该实验效果最好的方法。将本文SPH计算结果与文献[21]方法进行对比,发现本文方法产生的液滴更圆,粒子排布更为均匀,在水-气交界面处更为光滑,从而验证了本文基于密度权重计算表面张力公式的有效性。
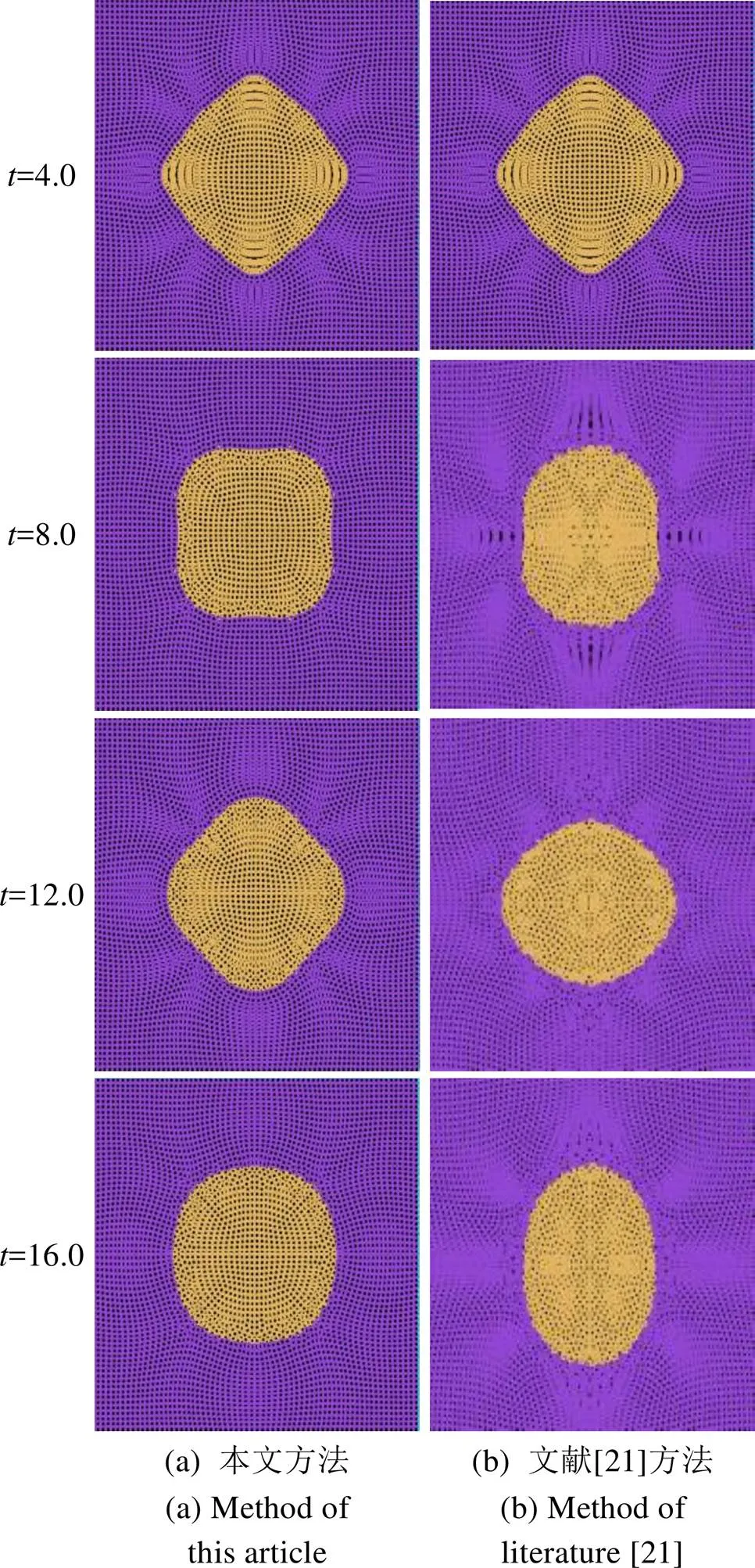
图12 圆形液滴形成变化过程效果图
本文主要针对于大密度比两相流进行研究,其中对称形式的压力梯度粒子近似公式主要适用于缓慢运动的两相流交界面处的压力梯度计算,而基于密度权重的表面张力计算主要适用于大密度比两相流在界面处剧烈运动,从而需要计算表面张力带来的影响的情况。本文尚未考虑是否可以将本文的方法应用到三相流甚至更多相流的流体模拟中,同时基于密度权重的表面张力计算主要针对的是二维情况下的方形液体变化情况,本文的方法是否可以拓展到三维,这些都将是今后研究的重点。
4 结 论
针对多相流界面处密度差导致界面压力与表面张力计算错误的问题,本文提出了一种新的压力梯度近似公式和改进的界面处人工斥力公式,保证了高密度流体与低密度流体在交界面两侧的压力对称,符合牛顿第三定律,使得多相流交界面更加清晰、光滑、无穿透。此外,本文还针对大密度比多相流(例如空气-水),给出基于密度权重的色函数计算公式,对交界面处的表面张力计算公式进行了改进;仿真试验结果表明,本文的表面张力计算公式在计算大密度比多相流交界面张力时,界面更加光滑,模拟效果更好。
[1] 柳有权, 刘学慧, 朱红斌, 等. 基于物理的流体模拟动画综述[J]. 计算机辅助几何设计与图形学学报, 2005, 17(12): 2581-2589. LIU Y Q, LIU X H, ZHU H B, et al. Physically based fluid simulation in computer animation[J]. Journal of Computer-Aided Design & Computer Graphics, 2005, 17(12): 2581-2589 (in Chinese).
[2] COLAGROSSI A, LANDRINI M. Numerical simulationof interfacial flows by smoothed particle hydrodynamics[J]. Journal of Computational Physics, 2003, 191(2): 448-475.
[3] MONAGHAN J J, KOCHARYAN A. SPH simulationof multi-phase flow[J]. Computer Physics Communications, 1995, 87(1-2): 225-235.
[4] HU X Y, ADAMS N A. A multi-phase SPH method for macroscopic and mesoscopic flows[J]. Journal of Computational Physics, 2006, 213(2): 844-861.
[5] HU X Y, ADAMS N A. An incompressible multi-phase SPH method[J]. Journal of Computational Physics, 2007, 227(1): 264-278.
[6] SOLENTHALER B, PAJAROLA R. Density contrast SPH interfaces[J]. In Proceedings of the 2008 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Eurographics Association. New York: IEEE Press, 2008: 211-218.
[7] MONAGHAN J J, RAFIEE A. A simple SPH algorithm for multi-fluid flow with high density ratios[J]. International Journal for Numerical Methods in Fluids, 2013, 71(5): 537-561.
[8] CHEN Z, ZONG Z, LIU M B, et al. An SPH model for multiphase flows with complex interfaces and large density differences[J]. Journal of Computational Physics, 2015, 283: 169-188.
[9] LIND S J, STANSBY P K, ROGERS B D. Incompressible-compressible flows with a transient discontinuous interface using smoothed particle hydrodynamics (SPH)[J]. Journal of Computational Physics, 2015, 309: 129-147.
[10] KRIMI A, REZOUG M, KHELLADI S, et al. Smoothed particle hydrodynamics: a consistent model for interfacial multiphase fluid flow simulations[J]. Journal of Computational Physics, 2018, 358: 53-87.
[11] 杨秋足, 徐绯, 王璐, 等. 一种基于黎曼解处理大密度比多相流SPH的改进算法[J]. 力学学报, 2019, 51(3): 730-742.YANG Q Z, XU F, WANG L, et al. An improved SPH algorithm for large density ratios multiphase flows based on riemann solution[J]. Chinese Journal of Thoretical and Applied Mechanics, 2019, 51(3): 730-742 (in Chinese).
[12] LUCY L B. A numerical approach to the testing of the fission hypothesis[J]. The Astrophysical Journal, 1977, 8(12): 1013-1024.
[13] GINGOLD R A, MONAGHAN J J. Smoothed particle hydrodynamics: theory and application to non-spherical stars[J]. Monthly Notices of the Royal Astronomical Society 1977, 181(3): 375-389.
[14] LIBERSKY L D, PETSCHEK A G. Smooth particle hydrodynamics with strength of materials[EB/OL]. [2020-03-10]. https://link.springer.com/chapter/10.1007% 2F3-540-54960-9_58.
[15] MONAGHAN J J. Simulating free surface flows with SPH[J]. Journal of Computational Physics, 1994, 110(2): 399-406.
[16] EDMONF Y M, SHAO S D. Simulation of near-shore solitary wave mechanics by an incompressible SPH method[J]. Applied Ocean Research, 2002, 24(5): 275-286.
[17] MONAGHAN J J, GINGOLD R A. Shock simulation by the particle method SPH[J]. Journal of Computational Physics, 1983, 52(2): 374-389.
[18] ADAMI S, HU X Y, ADAMS N A. A new surface-tension formulation for multi-phase SPH using a reproducing divergence approximation[J]. Journal of Computational Physics, 2010, 229(13): 5011-5021.
[19] LAWRIE A G W, DALZIEL S B. Turbulent diffusion in tall tubes. I. Models for Rayleigh-Taylor instability[J]. Physics of Fluids, 2011, 23(8): 3097.
[20] LOWE R J, ROTTMAN J W, LINDEN P F. The non-Boussinesq lock-exchange problem, Part 1 theory and experiments[J]. Journal of Fluid Mechanics, 2005, 537: 101-124.
[21] 沈雁鸣, 陈坚强. SPH方法对气液两相流自由界面运动的追踪模拟[J]. 空气动力学学报, 2012(2): 23-27, 34. SHEN Y M, CHEN J Q. Tracking simulation of free interface motion of gas-liquid two-phase flow by SPH method[J]. Acta Aerodynamica Sinica, 2012(2): 23-27, 34 (in Chinese).
Simulation of free interface motion of two-phase flow based on modified pressure and surface tension calculation
ZHU Xiao-lin, ZHOU Yun-ruo, HE Hong-hong
(School of Mathematics, Hefei University of Technology, Hefei Anhui230009, China)
In the simulation of multiphase flow using the smoothed particle hydrodynamics (SPH) method, the density of the multiphase flow at the interface was discontinuous, the pressure calculation of the particle interface was erroneous, and problems occurred, such as pressure oscillation at the interface and interface fracture. In response to the above problems, a new pressure gradient approximation formula and an improved artificial repulsion formula at the interface were proposed to make the interface clearer and smoother without penetration, thus producing better simulation results. In addition, by giving a color function calculation formula based on density weights, the formula was improved for the calculation of surface tension at the interface of multiphase flow with high density ratio, leading to the smoother density transition of multiphase flow interface and better simulation effect. Finally, through three simulation experiments, such as dam break, Rayleigh-Taylor interface instability, and non-Boussinesq locked exchange problem, the particle distribution map of the interface and the distance of the interface front at different times were obtained. The results can verify the rationality of the new pressure gradient approximation formula and the artificial repulsion formula at the interface. Through the simulation experiment of droplet formation in the air, the particle change diagram formed by the circular droplet was obtained, and the result can corroborate the effectiveness of the improved surface tension calculation method in this paper.
smoothed particle hydrodynamics method; multi-phase flow; pressure gradient particle approximation; artificial repulsion; the color function; surface Tension
TP 391
10.11996/JG.j.2095-302X.2020060970
A
2095-302X(2020)06-0970-10
2020-06-22;
2020-07-28
22 June,2020;
28 July,2020
国家自然科学基金项目(61272024)
National Natural Science Foundation of China (61272024)
朱晓临(1964-),男,安徽池州人,教授,博士,硕士生导师。主要研究方向为数值逼近、计算机图形学、CAGD、图形图像处理等。 E-mail:zxl_hfut@126.com
ZHU Xiao-lin (1964-), male, professor, Ph.D. His main research interests cover numerical approximation, computer graphics, CAGD and graphic image processing. E-mail:zxl_hfut@126.com

