谈谈立体几何位置关系证明问题中的通性通法
◇ 广东 孙仕兵
立体几何位置关系的证明是高考必考的考点,主要是“空间平行问题”和“空间垂直问题”的证明,而且这部分证明问题有时不能用空间向量来求解(因为能建系的条件一般都是为了求空间角附加的),即使能用空间向量求解,也需要进行逻辑推理.这样设置问题的目的是很明确的,即通过传统方法证明位置关系来考查相应知识点的掌握情况和直观想象、逻辑推理等数学核心素养.下面主要从通性通法的宏观和微观层面分析两种位置关系的证明.
1 从通性通法的宏观层面分析
通常从宏观上看,求解方法包括空间问题平面化和平面问题空间化.具体地说是两个框图(如图1).

图1
以“空间平行问题”为例,空间平行问题体现的是“直线与直线平行”“直线与平面平行”“平面与平面平行”三者之间相互转化,转化的依据就是相关的“判定定理”“性质定理”及“性质”,核心思想是“转化思想”.同时需要明确的是每类位置关系的判定中,重点是“直线与平面平行”和“直线与平面垂直”.下面从微观层面,仅以“空间平行问题”为例进行归纳和举例分析.
2 从通性通法的微观层面分析
2.1 直线与直线平行


2.2 直线与平面平行

2.3 平面与平面平行
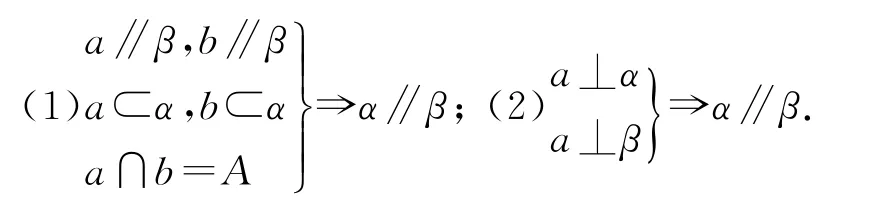
3 应用举例
例1已知:a∥α,a∥β,α∩β=b.求证:a∥b.
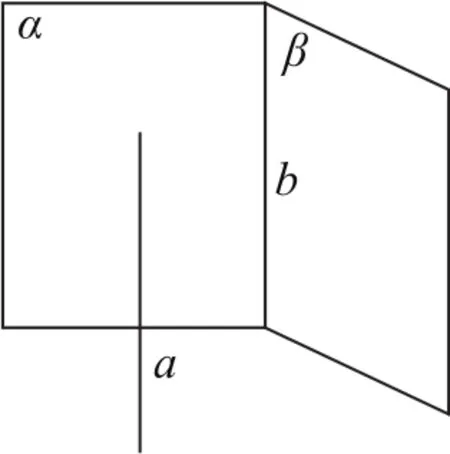
图2
分析要证明a∥b,只需在两个平面中选择一个平面,作直线c,使得a∥c,且c∥b.
根据a∥α,先作平面γ,使γ∩α=c,进而得a∥c,下面关键在于如何证明c∥b,由已知及直线与平面平行的性质定理易知,只需证明c∥β,这样在平面β内必须找出一条直线d,使得c∥d,余下的就是如何作直线d了,由a∥β易知,经过直线a作平面φ,使得φ∩β=d即可.
证明如图3,过直线a作平面γ和平面φ,使得γ∩α=c,φ∩β=d.

图3

从通性通法的角度讲,解答例1的关键因素是为了寻求“平行”,作了两条“交线”,即将平行相关的定理和性质融合在一起运用.空间平行问题,虽然分成三类,即直线与直线平行、直线与平面平行和平面与平面平行,但这三类不是孤立存在于解决问题的过程中,不难看出,在立体几何中证明直线与直线平行,除了“平行公理”,其他的转化依据都是直线与平面平行、直线与平面垂直及平面与平面平行的性质定理.还需要强调的是任何数学证明问题,从通性通法的角度看,解题的关键是从“结论”切入,然后按逻辑逐步进行分析,这样才能明确“为什么这么证明”,这种习惯的养成对核心素养中“逻辑推理”水平的提升起着至关重要的作用.
与空间平行有关问题的证明中,难点是运用“直线与平面平行的判定定理”来证明直线与平面平行.因为要证明直线与平面平行,只需证明平面外的直线a与平面内的直线b平行,但问题中,往往并没有直接给出直线b,所以需要我们去作这条直线.
例2如图4所示,S是平行四边形ABCD平面外一点,M,N分别是SA,BD上的点,且求证:MN∥平面SDC.
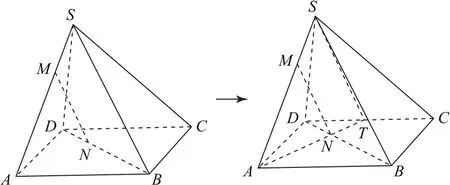
图4
分析要证明MN∥平面SDC,只需证明直线MN与平面SDC内一条直线平行,从已知图形中可以发现直线MN所在的平面AMN与平面SDC有一个公共点S,同时不难发现在平面AMN内还有一条直线AN与平面SDC有公共点,也就是连接AN并延长,交DC于T,再连接ST,则直线ST就是我们要作的“交线”!余下的就是要考虑如何证明直线MN平行于直线ST.通过已知条件中的比例线段,易推出两直线平行,证明部分略.
例3(2019年全国卷Ⅰ理18,节选)如图5所示,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N 分别是BC,BB1,A1D的中点.证明:MN∥平面C1DE.

图5
分析要证明MN∥平面C1DE,只需证明直线MN与平面C1DE内的一条直线平行,因为直线MN所在的平面A1MN与平面C1DE有公共点D,所以考虑延长A1M,看看是否能找到直线A1M与平面C1DE的公共点,即两个平面的另一个公共点.延长A1M交AB的延长线于点P,根据已知中的条件“E,M,N分别是BC,BB1,A1D的中点”,不难推出D,E,P三点共线,进而得出我们要作的交线就是直线DP(如图6).但仔细观察图形不难发现,图中的直线DE就是直线DP,进而我们发现了直线DE就是交线,但不作辅助线能否发现“直线DE就是交线”呢?其实发现的难度比较大(也可以说是思路的形成过程不是那么自然),因为只有发现了D,E,M,N四点共面才能确定直线DE就是我们要找的“交线”,只有连接了ME及B1C,再通过平行转化才能发现.所以这道题目中辅助线的作法,可以按如下方式去体现思维形成过程.
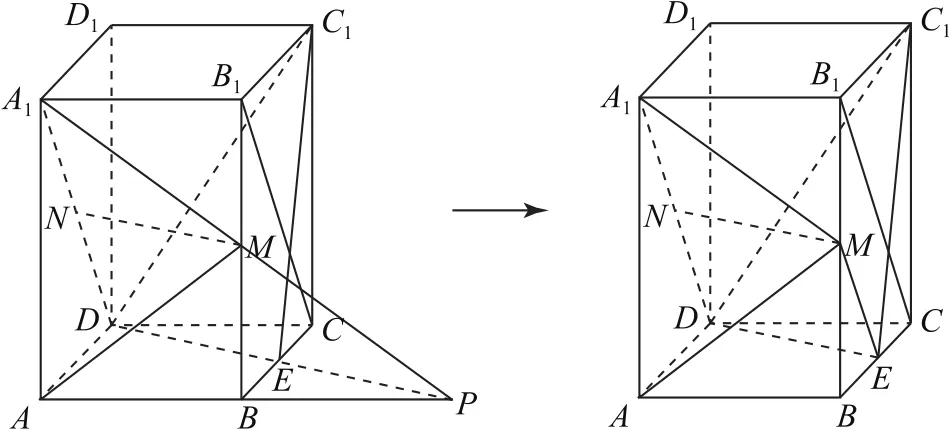
图6
按延长A1M方式作辅助线,很自然,应该提倡,但证明过程略有难度,因为要证“三点共线”,按“连接”方式作辅助线,虽然图形更加简洁,证明难度小,但分析思路有难度(较难发现DE就是我们要找的“交线”).鉴于以上两种方法的各自优点和缺点,还是提倡在演算纸上,先用第一种方式作完辅助线,在思考后才有可能发现第二种作法更简捷,进而正式答卷时用第二种辅助线的作法.
通过以上例题不难发现,立体几何中位置关系证明的难点是用判定定理证明“直线与平面平行”,因为在运用定理过程中,平面内的直线是隐藏着的,所以需要我们通过观察、分析挖掘这个隐藏着的直线.突破这个难点的通性通法就是“作交线”或“找交线”.
“提倡运用通性通法,建议淡化特技”是历年高考备考中反复倡导的理念,研究历年的高考真题也不难发现高考命题也是按照这种理念来命题的,所以在高考备考中,同样要注重运用“通性通法”解决问题,只有这样才能提高备考的质量,也符合目前的高考要求(即重点考查数学核心素养),从而避免陷入题海的深渊.

