融合信息技术突破数学建模教学环节的难点

摘 要:数学建模探究活动要求学生能运用所学知识解决实际数学问题,体验数学建模活动的完整过程.“茶水口感最佳问题”的教学要重点体现数据收集与处理,以及模型的选择、检验和求解的过程.在难点的突破中,要注重引导学生利用信息技术探究、比较和分析多种模型的选择方案.
关键词:数学建模;信息技术;模型选择
《普通高中数学课程标准(2017年版)》指出,数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养. 人教A版《普通高中教材·数学》(以下统称“教材”)必修第一册新增的数学建模案例“茶水口感最佳问题”就是一个很好的实例,体现了数学在人类生活、科学技术、社会发展中的应用. 同时,作为数学建模探究活动与学生初次接触,引起了教师的广泛关注,很多教学设计与反思都展现了数学建模案例的教学过程. 那么,这些教学设计是否都很好地突破了数学建模环节中的教学难点呢?这不免引起了笔者的思考.
一、“茶水口感最佳问题”教学难点突破中的问题
1. 教材情境呈现
情境:中国茶文化博大精深. 茶水的口感与茶叶类型和水的温度有关. 经验表明,某种绿茶用85°C的水泡制,再等到茶水温度降至60°C时饮用,可以产生最佳口感. 那么,在25°C室温下,刚泡好的茶水大约需要放置多长时间才能达到最佳饮用口感?
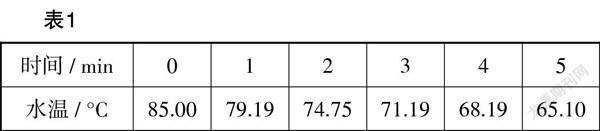
显然,如果能建立茶水温度随时间变化的函数模型,那么就能容易地解决这个问题. 为此,需要收集一些茶水温度随时间变化的数据,再利用这些数据建立适当的函数模型. 某研究人员每隔[1 min]测量一次茶水温度,得到表1的一组数据.
2.“选择函数模型”教学难点与实际处理方式
我们知道,建立函数模型解决实际问题的基本过程如图1所示. 根据数学建模素养的内涵,“茶水口感最佳问题”数学建模案例的教学重点可以设为将实际问题转化为数学问题、数据的收集与函数模型的选择和建立;教学难点可以设为数据的收集,函数模型的选择. 而在实际教学中,数学模型的选择却在很大程度上被忽视,很
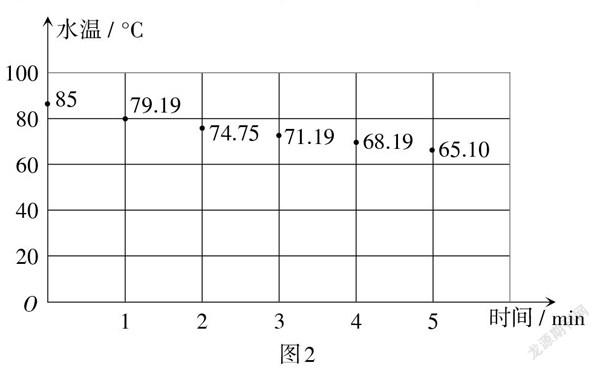
多教学过程都是“对照散点图分布,考虑到茶水温度降至室温不能再降的事实”直接就确定函数模型为 [y=kax+25 k∈R,0<a<1,x≥0]. 因此,在接下来的模型求解中,得到表1对应的散点图,如图2所示. 同时,根据教材的处理方式,对表1进行处理,得到表2.
如果取[a]的平均值0.922 7,就可以得到函数模型[y=60×0.922 7x+25 x≥0]. 将数值代入,就可以得到[x≈6.699 7 min].
整个教学过程好像都是按照“事先既定”的数学模型进行求解,至于在收集数据和选擇模型的环节,学生“如何选择模型”的教学过程呈现很少,甚至缺失.
3.“选择函数模型”应关注的实际教学问题
本节课的编写意图及教学建议指出,通过观察发现散点图的分布状况呈递减状态,学生可能会提出各种递减函数作为备选模型. 教师应引导学生注意到茶水温度降至室温就不能再降这一重要事实,再结合几类基本初等函数的变化特征,指导学生做出选择. 需要注意的是,实验所得的数据并不一定具有很强的规律性,函数模型的选择也是多样的,并不局限于指数型函数,所选择的函数一般也只能大致反应茶水温度变化的局部规律. 因此,建立模型后需要对模型进行检验. 教学建议还指出,建立模型与检验模型是实例教学的重点,除了教材提供的方法外,有条件的学校还可以指导学生利用信息技术工具选择拟合功能建立模型,并利用相关系数检验吻合程度,帮助学生建立合适的函数关系式,然后利用特定参数值验证模型,并解决实际问题. 因此,在“选择函数模型”的实际教学环节,完全可以从信息技术与数学教学融合的视角,就以下问题进行深入思考.
问题1:除了指数函数模型,还有其他拟合模型吗?如果有,与指数函数模型比较,拟合度分别怎么样?
问题2:基于茶水温度在降至室温后就不能再降的事实,教学中如何引导学生进行模型选择、比较和检验分析?
二、基于信息技术的模型选择,突破教学难点
基于问题1,笔者就我们学习过的函数模型及散点图来分析. 如果用线性模型、多项式模型或幂函数模型,与指数函数模型相比,谁的拟合度更高呢?采用不同的信息技术手段,对相关函数模型的拟合度进行了分析.
1. 采用WPS进行数据拟合
WPS有进行数据分析、算法的实现、函数模型拟合及图象与性质探究等功能,界面相对友好,操作方便,是教师和学生最熟悉的软件之一,其中包含了大量的函数、公式.
首先,新建一张WPS表格,分两列输入时间和温度数据(为了方便与上述函数模型对比,可以采用表2的数据处理). 其次,选中数据区域,点击“插入图表”中的“[xy]散点图”,然后点击散点图就会出现“图表元素”项目,如图3所示. 可以勾选“坐标轴”“数据标签”“趋势线”,在“趋势线”下会有属性栏“线性”“指数”“多项式”“幂”等选项,如图4所示.
分别点击“线性”“指数”“多项式”等选项,相应勾选“显示公式”“显示[R]平方值”,就会显示图4中的相关信息,得到线性模型[y-25=-3.887 4x+58.622],[R2=0.982],指数函数模型[y-25=59.053e-0.079x],[R2=][0.993 5],多项式模型[y-25=0.345 7x2-5.616x+59.774],[R2=0.998 6]. 我们知道,在数学统计中,用[R2=1-][i=1nyi-y2i=1nyi-y2]来刻画拟合效果,[R2]的值越大,拟合效果越好. 从而可知多项式模型的拟合效果最好. 其中,指数模型拟合与模型[fx=60×0.922 7x+25 x≥0]有些许差别,因为是信息技术工具通过估算得到的. 事实上,[e-0.079=0.924 04],但是在WPS中不方便直接计算[fx=60×0.922 7x+25 x≥0]的拟合度. 另外,在散点图中去掉[0,60]这个点后可以采用幂函数模型进行拟合,得到[y-25=55.248x-0.182,R2=0.962 8]. 因此,可以将通过上面各个模型得到的最佳饮用时间的[x]值列表,如表3所示.
从表3发现,四种模型的拟合度都十分不错. 其中,虽然多项式模型的拟合度最高,但是在基于“60℃饮用口感最佳”的假设下最佳饮用时间不存在;幂函数模型达到最佳口感经历时间最长. 从数据来看,还不能完全回答问题1中的所有疑问. 因为基于WPS的数据分析,不能反映出各模型的函数图象变化趋势,也不能对原模型[fx=60×0.922 7x+25 x≥0]的拟合度进行估算. 因此,还需要借助GeoGebra软件进行数据拟合再分析.
2. 采用“GeoGebra經典”数据拟合
GeoGebra是一款十分重要的数学软件. 它具有字母的逻辑运算、统计、微积分等功能,集几何图形、数据处理、代数运算于一体.
启动“GeoGebra经典6”,在表格区域输入表2的数据. 构造点列,软件会将点列自动记为“[l]1”,图形区域也会画出散点图. 在命令输入栏输入“指数拟合”,得到指数函数模型[y=59.053e-0.079x]. 在命令输入栏输入“可决系数[R]方[l1,f]”,得到关于[fx]的[R2]的值[0.993 5]. 继续输入函数模型[qx=60×0.922 7x]及“可决系数[R]方[l1,q]”,得到函数模型[y=60×0.922 7x+][25 x≥0]的[R2]的值[0.984 7],如图5所示. 同样地,在命令栏分别输入“多项式拟合[l1,1]”“可决系数[R]方[l1,h]”“多项式拟合[l1,2]”“可决系数[R]方[l1,g]”,就会得到线性模型和二次多项式模型. 去掉点[0,60]构造新点列[l2],输入幂函数拟合就会得到幂函数拟合模型,具体数值与WPS的数据都一致. 通过GeoGebra软件不仅能方便地看到各个模型的拟合程度,还能了解每个模型的曲线形状,如图6所示. 从而一目了然地排除一些不符合实际条件的假设模型. 例如,二次多项式模型中最低点的值(即因变量的值)约不低于38°C;幂函数模型由于下降趋势平稳,长时间内因变量的值可能不会低于20°C. 这就是表3中的二次多项式模型无解与幂函数模型时间长的原因,也充分说明了模型的选择要与现实情况相结合,是对问题2的直观回答.
3. 线性模型与指数模型的检验分析
根据情境假设,60℃是茶水饮用效果最佳的关键点. 教学中,教师和学生有必要思考在大于60℃这个高温区间内的数据检验与分析情况.
在选择模型的过程中,如果缺少在大于60℃这个高温区间内对线性模型的分析与比较,就没有很好地突破教学难点的表现. 为什么这样说呢?
首先,从表3中可以发现,线性模型与教材中估算得到的函数模型[y=60×0.922 7x+25 x≥0]的拟合度[R2]分别为0.982和[0.984 7],得到最佳饮用时间分别为[6.077]和[6.699 7],这两个结果是十分接近的.
其次,我们知道,水在温度较高时,温度随时间下降较快,当温度接近室温时,温度下降越来越慢,从而在大于60℃这个高温区间内,结合采集的6组数据散点图,学生很有可能采用线性模型进行求解.
最后,表2中的温度和时间的数据线性相关性很强,不妨利用Excel(或WPS)中的“数据分析”进行线性回归分析,如图7所示.
图7的数据表明,水在高温区间(大于等于60℃)时,时间与温度的线性相关系数为0.99,从而线性相关性是非常强的. 同时,[P=0.000 122<0.001],说明线性回归效果显著性水平十分明显,置信度达到99.9%以上. 这都说明有足够的理由需要在大于60℃这个高温区间内对线性模型进行分析. 基于此分析,结合“茶水温度在降至室温就不能再降的事实”,比较之后选择指数函数模型,教学过程更为自然.
三、反思与教学建议
用函数构建数学模型解决实际问题时,除了对变化过程中的常量、变量及相互关系进行分析之外,数据收集、数据处理和数据分析的过程也显得尤为重要. 数学建模教学中包含复杂的数据采集与分析、多种建模求解方案的尝试,是一个不断探索、创新、完善和提高的过程. 那么,如何更好地开展高中数学建模探究活动教学呢?
1. 根据不同问题的相应特征收集尽可能多的数据
在组织学生开展数学建模活动时,需要根据不同问题的相应特征收集尽可能多的数据. 教材中的案例给出了6组数据,在实际教学中还可以根据茶水冷却时间的快慢收集更多数据.
2. 引导学生进行不同数学模型的探究活动
不同的探究方向往往能触发学生的创新思维,培养学生的创新意识. 因此,在解决问题的过程中,要引导学生进行不同数学模型的探究活动,让学生经历不同数学模型对结果带来的影响.
3. 选取能用确定的标准来衡量的实际问题
在数学建模教学初期选题时,尽量选取能用确定的标准来衡量的实际问题. 情境中所谓的“口感最佳”的数学本质实际上就是计算温度在60℃时建立的数学模型的函数值.
4. 引导学生了解要解决问题的相关背景
在数学建模教学时,要引导学生了解要解决问题的相关背景(如饮茶文化的相关知识). 实际上,学生对饮茶文化的相关知识并没有生活积累. 曾有国外专家研究,饮用65℃ ~ 69℃茶的人群,患食道癌的风险是饮用温度低于65℃茶者的2倍;再有研究表明,食道的黏膜只能耐受50℃ ~ 60℃的温度,超过这个温度范围就会被烫伤,而60℃恰好处于临界点.
在数学建模教学时,还要注重与信息技术的融合. 信息技术能提高学生学习数学的兴趣和应用数学的意识与能力,尽量引导学生利用熟悉的数学软件及WPS处理数据的意识,将数学、计算机有机地结合起来,解决实际生活中的问题.
参考文献:
[1]中华人民共和国教育部制定. 普通高中数学课程标准(2017年版)[M]. 北京:人民教育出版社,2018.
[2]周威. 例谈回归分析在学校评价中的实际应用[J]. 中学数学,2015(5):49-50.
收稿日期:2021-06-23
基金项目:湖北省教育科学规划课题——基于课程标准的教学与质量测评研究(2020JB348);
恩施州教育科学规划课题——区域教研中推进高中数学教师践行课程标准的教学与质量测评研究(ZGH202045).
作者简介:周威(1985— ),男,中学一级教师,主要从事高中数学教研与质量测评研究.

