弗赖登塔尔的数学教育思想及其再发展

王海青　曹广福

摘  要：数学化、数学现实与有指导的再创造体现了数学教育家弗赖登塔尔的重要教育思想. 此外，强调教充满联系的整体知识结构也是弗赖登塔尔数学教育思想的重要组成部分. 在现今学校按学科教学又注重STEM教育的大环境下，注重对知识整体结构的获得有助于学生更好地理解知识的本质并促进学习的迁移. 问题驱动教学与发生教学法可以看作是对弗赖登塔尔数学教育思想的具体实践和进一步发展，它们强调揭示数学知识的教学价值与本质，注重教学生学会思考.

关键词：弗赖登塔尔;数学化;问题驱动;HPM思想;发生教学法

一、弗赖登塔尔的数学教育思想再探

著名荷兰数学教育家弗赖登塔尔（Freudenthal H，1905—1990）对数学教育有着特别的理解，其著作《作为教育任务的数学》《数学教育再探》《播种与除草》集中阐述了他的数学教育思想，核心观点体现在三个方面——数学化、数学现实、有指导的再创造.

20世纪末，荷兰的弗赖登塔尔数学研究所根据其教育理念开发了一套高中数学教材并用于课堂实验. 教材编写确立了5个具体目标：揭示数学与物理、化学和生物科学之间的联系;掌握物理、化学和生物科学所需要的基本数学语言;理解数学无论过去和现在都是一项人类活动;运用图形计算器和Cabri等数学软件;实现数学化. 实验教材编写目标反映了数学作为人类的一项活动与现实世界的密切联系，强调每个知识点的教学都要充分考虑数学与现实的联系，并通过“数学化”来组织教学. 研读弗赖登塔尔的数学教育专著与其实验教材编写的目标，发现数学化、数学现实与有指导的再创造是弗赖登塔尔数学教育思想的重要体现. 除此以外，强调对学习材料进行整体设计以突出相互间的联系也是弗赖登塔尔数学教育思想的重要组成部分，这一点在以往的相关研究中较少提及.

1. 数学教育思想1——数学化

初等数学的知识体系与现实世界密切相关，大都能在实际生活中找到相应的背景或问题. 因此，对数学基础的建立最适合的开始应该是常识. 这里的常识是指学习者的数学经验或生活经验. 也就是说教学应结合学生的实际提出问题，并建立起与数学的联系，进而运用数学的思想方法分析和解决问题，揭示规律或本质、形成概念或原理，即用数学方法把实际材料组织起来，这个过程被称为“数学化”.“实际材料”或问题情境除了日常生活实际背景，还有自然科学情境或纯数学情境. 弗赖登塔尔强调任何数学都是数学化的结果，学数学就应该是体验数学化的过程.

数学化分为横向数学化与纵向数学化，或称之为水平生活化与垂直生活化. 将现实世界的問题抽象为数学的模型或图式（函数或方程、代数符号、路线图、几何图形、表格等）的过程称为横向数学化;运用数学的思想与方法处理数学问题的过程称为纵向数学化. 也就是说，横向数学化就是将实际问题转化为数学问题，建立起数学与外部世界的联系;纵向数学化是从不同角度、利用不同方式表征数学问题，用多种方法分析和解决问题以抽象归纳出一般规律揭示本质的过程，是在数学内部建立起丰富联系. 由此可见，横向数学化与纵向数学化是教学组织过程中密不可分的有机整体.

2. 数学教育思想2——数学现实

数学教学数学化是将现实数学化——现实的许多片断. 这里的现实是指学生自己的数学现实（Realistic Mathematics Education，简称RME），是每个人所接触到的客观世界中的数学规律及有关这些规律的数学知识结构，也就是学生已有的生活经验和数学基础. 数学化教学的过程是在教师的引导下学生根据自己的数学现实处理实际问题，进一步组织、抽象、扩展，从而形成新的数学现实的过程.

因此，数学的学习应该是从现实情境开始的探索活动. 自然地，数学教学则需要从学生的数学现实而非形式化的数学系统出发生成知识、习得思想. 依据数学知识产生的背景，提供给学生探索的现实情境或材料可以有来自日常生活、自然科学或者数学本身的情境，但都应该是学生能理解和接受的真实情境. 真实的数学活动有助于促进学生的有效学习，实现学生对知识的灵活运用与迁移.

3. 数学教育思想3——有指导的再创造

根据数学公理化的特征，数学教材基本上是以逻辑的形式化的演绎体系呈现，按照概念、定理、性质与法则、例题与习题的顺序编写教材内容，而知识产生与思想形成的原因，以及数学家在解决各种问题过程中所反映出来的研究精神与思维品质等则鲜有见之. 正如弗赖登塔尔所言，没有一种数学思想，以它被发现时的那个样子发表出来. 一个问题被解决以后，相应地发展成一种形式化的技巧，结果使得火热的思考变成了冰冷的美丽.

弗赖登塔尔主张教师结合数学史来重新组织教材内容以更加适合学生的学习，并将数学作为一种活动进行分析和解释. 建立在这一基础上的教学方法称为再创造. 依据历史再创造教材内容并非要重复人类的全部学习过程，而是让学生经历经过改良且有更好引导意义的历史过程，重走历史上数学知识产生的几个重要步骤. 也就是说教学过程应反映在教师的指导下学生面对新情境是怎样运用已有的知识结构分析问题和解决问题，并发现和归纳出新知识的过程.

4. 数学教育思想4——整体设计

数学化、数学现实、有指导的再创造，三个核心思想彼此相互实现、互为融合. 数学化是最重要的数学教学方式，让学生经历数学化的过程首先需要教师依据数学史剖析教材内容对其进行重组再创造，并结合学生的数学现实创设适当的问题情境，引导学生在情境中进行探究活动并经历完整的数学化过程. 为了促进学习的有效迁移，在横向数学化与纵向数学化的过程中，教师要突出知识间的丰富联系，重视对数学整体结构的教学. 换句话说，弗赖登塔尔的数学教育思想中也蕴含了深刻的整体教学观念.

（1）教充满联系的数学.

强调按各个课时的内容逻辑来设计的教学往往会导致知识的片断化与碎片化. 教材的编写重视数学内部的联系以构建单元知识结构，却又牺牲了数学与外部的联系. 与外部相关的情境即便是有，也更像是起点缀作用的布景，与数学真正的联系很少. 弗赖登塔尔赞成人们学习的每件事情都应该是充满联系的，认为教学不要教孤立的片断，而要教连贯的材料. 连贯的材料是指具有多方面联系的、符合学生数学现实的材料. 学生获得有丰富联系的与现实有关的知识，才能形成良好的认知结构有助于长时记忆，才能有效培养学生的应用意识促进学习的迁移.

弗赖登塔尔所指的联系涉及两个方面：数学学科内部之间的联系，数学与外部的联系. 他把学习过程作为一个整体进行考虑，认为学习各要素的结合应当被组织得尽可能早、尽可能长和尽可能强. 例如，函数、图象、方程应该看作是交织缠绕在一起的各个学习分支，而代數与几何之间的互动交织也不必只限定在解析几何上. 但是弗赖登塔尔强调数学概念与原理的教学要先考虑数学与学生的生活现实及数学基础的联系. 与数学联系的外部现实内容可以是日常生活的、自然的、物理的、化学的或者数学本身的材料. 教师在具体教学中要做的是引领学生在现实中“做数学”“用数学”，逐步发展为充满联系的看似与现实没有联系的形式化数学体系. 教充满联系的数学也就是要让学生充分经历横向数学化与纵向数学化的过程.

（2）按照数学的整体结构进行教学.

弗赖登塔尔认为，传统的教学理论主要聚焦于局部分析具体的教学内容，还没有按照数学的整体结构来进行教学. 即便是现在，一线的数学教学情况似乎也没有太大的改观. 数学依附于现实，因此数学的整体结构也应该存在于现实之中. 这里的整体结构不是指数学已有的现成的演绎体系，而是学生随着学习过程中数学的发展而不断发展变化的动态的整体知识结构，它应与现实世界充满各种有机联系. 强调按照数学的整体结构来进行教学的实质就是要结合学生的数学现实教充满各种联系的数学，才能使学生获得一个随着学习不断更新优化的、与现实密切结合的整体知识结构，并将之应用于现实. 需再次明确的是，这里的现实是指学生已有的生活经验与数学知识基础.

怎样才是按照数学的整体结构来进行教学呢？弗赖登塔尔指出，数学化地组织一个教学内容或一个领域是最为正确的方式. 因为将数学解释为一种活动的话，就必须通过数学化来教数学、学数学. 先利用恰当的现实问题情境（数学内容的或者是非数学内容的）建立起现实世界与数学世界的初步联系，通过建模将要学习的内容与数学内部或外部联系起来. 这个过程也就是横向数学化的过程. 仅满足于现实情境与数学的联系显然是不够的. 下一步是引导学生利用类比、归纳、演绎等方式经历抽象化、形式化的过程，将新的知识在数学内部建立起各种关系，使之有机融入旧的知识体系，进而形成新的整体认知结构. 这就是纵向数学化的过程，是更高一级的在数学的形式体系上的联系. 没有经历从现实世界到数学世界的建模过程，就没有经历真正的横向数学化，获得的知识难以应用于实际. 而没有经过深度的纵向数学化使概念与原理在数学内部建立紧密的联系，习得的知识将是一盘散沙. 用数学化组织一个领域，有助于学生整体地看待数学知识与把握知识间的联系，既见“树木”又见“森林”. 通过数学化组织一个领域，学生习得的整体知识结构才是牢靠的、灵活的和可利用的，既可以在数学内部自由转换，又可以应用于现实解决问题.

如果说数学化是数学教学最重要甚至是唯一的方式，实施数学化的途径是结合历史和学生的数学现实对教学内容的再创造，那么“教学内容是否充满了各种联系”与“是否被有机地组织到所处的领域”则是判断横向数学化与纵向数学化程度的重要指标，是判断学生所习得的数学整体知识结构是否完善的重要标准. 换言之，教师依据数学史与学生的数学现实对教学内容进行再创造，以数学化的方式组织教学，其目标是要教给学生充满联系的数学，并能将之有效整合到所处的领域. 在当今按学科、模块、知识点教学的学校教育大环境下，强调以单元为主体对教学内容进行整体设计能解决课时之间的零散性与知识之间的孤立性、单元之间的割裂性与学科之间的无关联性等问题，从而更好地揭示知识的本质、突出思想与应用，有助于学生把握知识的整体结构，促进学习的迁移并养成STEM素养. 因此，弗赖登塔尔的整体教学观念对于如今的基础教育数学课程与教学改革依然有重要的启示和参考作用.

二、弗赖登塔尔数学教育思想的再发展

1. HPM思想与发生教学法

数学史与数学教学关系国际研究小组（International Study Group on the Relations between History and Pedagogy of Mathematics，简称HPM）成立于1972年的第二届国际数学教育大会. 在国内，关于HPM思想与教学的研究成果主要集结在著作《HPM：数学史与数学教育》中，作者对HPM的历史渊源、哲学基础及相应的教学法进行了深入研究与探索，并开发出大量数学教学案例. HPM思想强调数学教学应该重走发现之路. 法国数学家庞加莱（H.Poincaré，1854—1912）就认为，数学课程的内容应完全按照数学史上同样内容的发展顺序展现给学生. Radford等根据历史发生原理和学习心理学理论提出了基于历史的课堂活动设计方法的理论框架，如图1所示. 指出数学教学设计要整体思考数学的历史发展、教学的方法与学生的心理三个方面.

HPM研究的主要目标是通过数学史了解知识产生的过程与数学家所遇到的困难，从而获得启示，更好地组织教材内容以适合学生的学习，这与弗赖登塔尔的再创造思想恰好有着共通之处. HPM主张用发生教学法（the genetic approach to teaching and learning）组织数学教学，通过数学史寻找学生学习的最佳方式. 发生教学法继承了逻辑演绎和历史方法论的优点，既重视演绎的结果，也强调产生结果的问题本源. 它通过梳理历史整体理解数学知识与思想的生成过程，以及蕴含其中的重要价值，进而根据问题重构教材内容组织教学. 发生教学法一般遵循以下几个步骤：了解所讲授主题的历史;确定历史发展过程中的关键环节;重构这些环节，使其适合课堂教学;设计出一系列由易至难的问题，后面的问题应建立在前面问题的基础之上. 因此，发生教学法重视依据历史设计问题序列，重视问题驱动与问题解决，由问题导出结论. 运用发生教学法进行数学教学与组织，要求教师具备一定的数学史知识，并且具有恰当选择数学史材料、将史料转化为学生能理解的学习材料、将数学史料与教学内容有机融合促进教学的能力.

2. 问题驱动教学法

数学具有二重性：以符号化、抽象化、形式化表现出来的“冰冷”数学结果和数学家在发现问题、分析问题与解决问题时所表现出来的“火热”思考过程. 数学教材则基本上按照概念、定理、性质与法则、例题与习题的顺序呈现教学内容. 这使学生在一系列严谨的、形式化的知识堆砌中难以体会到数学知识间所蕴含的丰富联系及其重要价值和作用，不知数学知识从何而来为何而去，因而有了数学无用的论调. 但数学并不是按照现在教材中的方式发展的. 问题是促进学科发展的原始动力，数学也不例外. M.克莱因（Morris Kline，1908—1992）就曾指出，每一个数学分支均是为攻克一类问题而发展起来的. 因此，以问题驱动教学，能再现数学“火热”的思考过程，教师引导学生在问题空间中探索生成概念与原理、习得思想与方法，在抽象一般规律揭示本质的过程中教学生学会思考. 张奠宙先生在90年代就倡导以问题驱动的新概念数学，李大潜院士也提倡在应用数学研究领域要重视问题驱动，由问题推动科学研究，《问题驱动的中学数学课堂教学·理论与实践卷》一书更是对问题驱动数学教学进行了系统阐述.

问题驱动教学法的关键是教师能否依据历史为教学内容创设合适的问题及情境. 从历史发展来看，数学是在解决各种现实问题和内部逻辑矛盾的过程中不断形成、发展和完善的，但外部动因是数学最根本的发展动力. 因此，驱动数学教学的问题可以是生活问题、现实问题或数学问题，只要它是具有启发性的、本原性的、触及数学本质的、能够在教学中起统帅作用的问题. 但是问题不等于问题情境，只有当学生有解决它的欲望时，问题才能构成问题情境. 因此，教师还要结合学生的数学现实——已有的生活经验和数学基础，创设能激发学生兴趣和求知欲望的情境材料，并将数学问题有机融入相应的情境当中. 所创设的问题情境是否真实有效就看它是否具有一定的生活意义、数学价值或科学价值.

问题驱动教学强调围绕能反映数学本质的核心问题展开教学探究活动，并将问题寓于学生能理解的情境之中，引导并启发学生在发现与提出问题、分析与解决问题的过程中生成数学知识与思想方法. 这里的问题是指促成数学知识形成的本原性问题，而不是为启发学生思考或突破教学重、难点而设置的一系列环环相扣的问题链. 两者本质不同但也有密切联系. 为引导学生对核心问题进行有效探究，教师在组织教学的过程中需要根据学生的反应设置有针对性的、有启发性的和有前后逻辑关系的一个个小问题，即问题链，将大的核心问题转化为有递进关系的小问题来解决.

3. 弗赖登塔尔数学教育思想与发生教学法、问题驱动教学法的关系

数学化、数学现实、再创造和整体设计是弗赖登塔尔的主要数学教育理论观点，强调对数学本原的探求. 弗赖登塔尔冀望教师依据历史结合学生实际重组教材，让学生在做数学、用数学的过程中获得数学，实现对数学的有限再创造. 因此，发生教学法和问题驱动教学法是弗赖登塔尔数学教育思想在教学中的两种具体实践方式，也是对其思想的进一步发展. 两者都强调学生在教师的引导下对数学知识进行有限的再创造，生成新知并揭示其思想.

问题驱动教学法与发生教学法有着紧密联系，但是也各有侧重. 首先，两者重视对数学内容本质的剖析与其背后思想及方法的挖掘;其次，两者强调数学史对教学的重要指导作用，重视从历史中获得启示预测学生可能发生的学习困难与障碍，进而再创造教材内容确定教学思路;再次，两者注重通过数学化来揭示数学本质，反映数学的规律性与思想性. 最后，两者都关注学生的数学现实对教学的影响作用，重视对教学问题及其情境的设计，并引领学生经历再发现、再创造数学的过程.

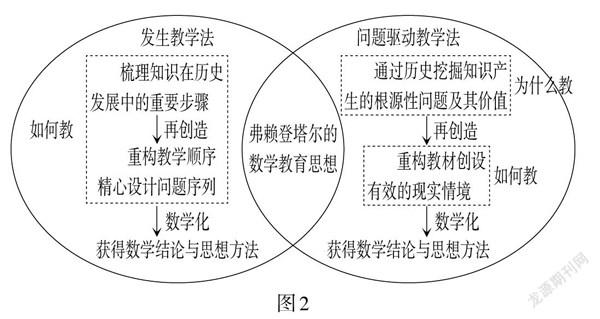
但是发生教学法主要是通过梳理历史以整体理解知识的生成过程，进而以逻辑的、更符合学生认知规律或特点的方式开展教学，意在如何教. 而问题驱动教学法则是通过追溯历史揭示知识背后的思想与价值，挖掘其产生的背景、缘由及其与其他知识间的联系，强调为什么教. 进而基于对数学史和教材内容的理解设置合适的问题情境，把教材上数学的学术形态转化为学生容易接受的教育形态，从关注为什么教转向如何教. 此外，雖然两种教学法都强调对问题的设计，但问题的涵义不尽相同. 发生教学法强调问题驱动与问题序列，这里的问题是一系列由易至难的问题，是层层递进的问题链. 问题驱动教学法所强调的问题是指促使知识产生的、能体现其本质和起统领作用的原始问题，教学则围绕着这个核心问题展开探究活动生成新知. 图2可以直观反映出发生教学法与问题驱动教学法的关系.

参考文献：

[1]乔爱萍. 论弗赖登塔尔数学教育思想的现实意义[J]. 江苏教育研究，2014（2）：51-55.

[2]王彦飞，宋婷. 试析弗赖登塔尔的数学教育思想及其对儿童数学教育的启示[J]. 教育探索，2016（2）：7-10.

[3]蒲淑萍，汪晓勤. 弗赖登塔尔的HPM思想及其教学启示[J]. 数学教育学报，2011，20（6）：20-24.

[4]付云菲. 弗赖登塔尔的数学教育思想研究[D]. 呼和浩特：内蒙古师范大学，2013.

[5]孙晓天. Freudenthal研究所开发的新高中数学课程[J]. 数学通报，2001（11）：41-44.

[6]弗赖登塔尔. 数学教育再探[M]. 陈昌平，唐瑞芬，译. 上海：上海教育出版社，1999.

[7]弗赖登塔尔. 作为教育任务的数学[M]. 陈昌平，唐瑞芬，译. 上海：上海教育出版社，1995.

[8]张国祥. 数学化与数学现实思想[J]. 数学教育学报，2005（1）：35-37.

[9]孙晓天. 现实数学教育的思想基础及其基本概念[J]. 学科教育，1995（9）：16-19，22.

[10]张奠宙，唐瑞芬，刘鸿坤. 数学教育学[M]. 南昌：江西教育出版社，1991.

[11]FREUDENTAL H. Didactical Phenomenology of Mathematical Structures[M]. Dordrecht：Reidel Publishing Company，1983.

[12]PÓLYA G. Mathematical Discovery：on Understanding，Learning，and Teaching Problem Solving（Vol.2）[M]. New York：John Wiley & Sons，1965.

[13]徐章韬，汪晓勤，梅全雄. 发生教学法：从历史到课堂[J]. 数学教育学报，2010，19（1）：10-12.

[14]汪晓勤. HPM：数学史与数学教育[M]. 北京：科学出版社，2017.

[15]M KLINE. Logic Versus Pedagogy[J]. American Mathematical Monthly，1970，77（3）：264-282.

[16]M KLINE. The Ancients Versus the Moderns：a New Battle of the Books[J]. Mathematics Teacher，1958，51（6）：418-427.

[17]吴俊，汪晓勤. 发生教学法：从理论到实践[J]. 教育理论与实践，2013，33（2）：3-5.

[18]张奠宙，张荫南. 新概念：用问题驱动的数学教学[J]. 高等数学研究，2004，7（3）：8-10.

[19]邓纳姆. 微积分的历程——从牛顿到勒贝格[M]. 李伯民，王军，张怀勇，译. 北京：人民邮电出版社，2010.

[20]M KLINE. Calculus：An Intuitive and Physical Approach[M]. New York：Dover Publications，Inc，1998.

[21]高雪芬，汪晓勤. M.克莱因的HPM思想：以《微积分》为例[J]. 数学教育学报，2012，21（4）：24-27.

[22]波利亚. 数学的发现——对解题的理解、研究和讲授[M]. 刘景麟，曹之江，邹清莲，译. 北京：科学出版社，2010.

[23]李大潛. 从数学建模到问题驱动的应用数学[J]. 数学建模及其应用，2014，3（3）：1-9.

[24]曹广福，张蜀青. 问题驱动的中学数学课堂教学·理论与实践卷[M]. 北京：清华大学出版社，2018.

[25]郑毓信.“问题意识”与数学教师的专业成长例[J]. 数学教育学报，2017，26（5）：1-5，92.

[26]曹广福，张蜀青. 论数学课堂教学与评价的核心要素：以高中导数概念课为例[J]. 数学教育学报，2016，25（4）：17-20.

收稿日期：2021-06-27

基金项目：广东省普通高校特色创新类项目——指向深度学习的问题驱动教学研究（2021WTSCX089）;

广东省教育科学“十三五”规划研究项目——新师范背景下“U-G-S”校地数学教师教育共同体的构建及其运行机制探索（2020GXJK410）.

作者简介：王海青（1978— ），女，博士，副教授，主要从事数学史与数学教育研究.