基于数学学科核心素养的课堂教学实践

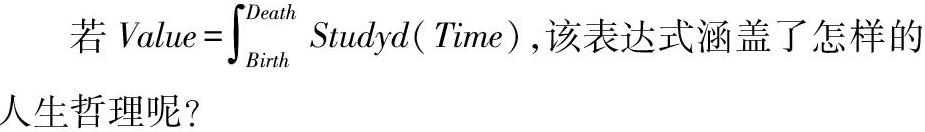
摘 要：在高校数学课堂上，围绕数学学科核心素养进行教学实践是落实课程思政，发挥课程立德树人功能的主要途径。文章以定积分的概念为例，通过具体的课堂教学实践，延伸定积分概念的人文内涵，蕴含着课程思政目标，展现出数学课在培养学生核心素养过程中的独特功能。

关键词：数学核心素养;课堂教学;课程思政;定积分

全国职业教育大会在北京召开，会上传达了坚持立德树人，优化类型定位，加快构建现代职业教育体系。立德树人必然是职业教育育人工作的根本任务，学科核心素养正是学科育人价值的集中体现。曲元海等在《高等数学核心素养探析》一文中对微积分核心素养进行了界定，以极限、微元法为核心思想，以微积分、极限运算为核心能力的素养，叫作高等数学核心素养。《高等学校课程思政建设指导纲要》中指出，理学、工学类专业课程，要在课程教学中把马克思主义立场观点方法的教育与科学精神的培养结合起来，提高学生正确认识问题、分析问题和解决问题的能力。在高职数学的教学过程中，要注重科学伦理教育和数学思维方法的训练，培养学生探索新知、追求真理、勇攀高峰的责任感和使命感，培养学生精益求精的大国工匠精神。

高校数学学科核心素养的提升，抓手在课堂，于是基于数学学科核心素养的课堂教学实践势在必行。微积分运算是学生学习高等数学后能够获得的一种核心能力，而定积分是微积分中的重要内容，因此，需要教师深入挖掘该知识在培养学生核心素养中的作用，从而提升该课程的育人效果。本文以定积分的概念为例，挖掘其与核心素养相关联的知识和方法，并分享其中的实践经验。教学设计以职教云平台为基础，分为课前、课中和课后三个环节，教学时长建议为1学时，设计思路是将核心素养的培养目标融入相应的教学资源和活动，使教学内容更加通俗易懂，提升学生学习数学积极性的同时，体现出数学的价值。

一、课前

定积分是一个新章节，我们为同学们准备了一篇关于定积分发展史的课件，上传至职教云平台课前环节，让学生充分了解微积分的历史和演变过程，带着对定积分强大功能的神秘感开启本次课的学习。

在大多数科学里，一代人要推到另一代人所修筑的东西，一个人所创立的要被另一个人取代，只有数学，每一个人都能在旧体系上增加一点色彩。微积分学作为数学的一个重要分支，其发展史正印证了这句话。微积分学是微分学和积分学的总称，它是一种数学思想，“微分”就是无限细分，“积分”就是无限求和。课件从准备、创立、完成和发展等四个阶段详细介绍了微积分的发展史。

积分的发展是漫长而缓慢的，其发展的动力来源于实际应用中的需求，通过数学家的不懈努力，使得积分体系越来越完善，同时运用该知识可以解决更多的实际问题。例如，积分知识中包含这用离散过程逼近连续，以直代曲（本次课将设计该思想）等思想，不仅是数学史上，甚至是科学思想史上的重要创举。

二、课中

上课后对本次课的平台签到情况进行统计，记录学生未签到原因。

守时是一种素质，是职业道德的一个基本要求;无法按时上课的，要走相应的请假流程，无规矩不成方圆。因此，上课按时签到，事虽小，却能体现出一个人的职业道德水平，正是“细节之处见修养”。

第一步：知识回顾

通过开展不定积分知识小测验（内容关于基本积分公式和运算性质），让学生回顾基本积分公式及其简单计算，熟悉不定积分的书写要求，以便通过对比，加深对定积分表达式的理解。

第二步：导入新课

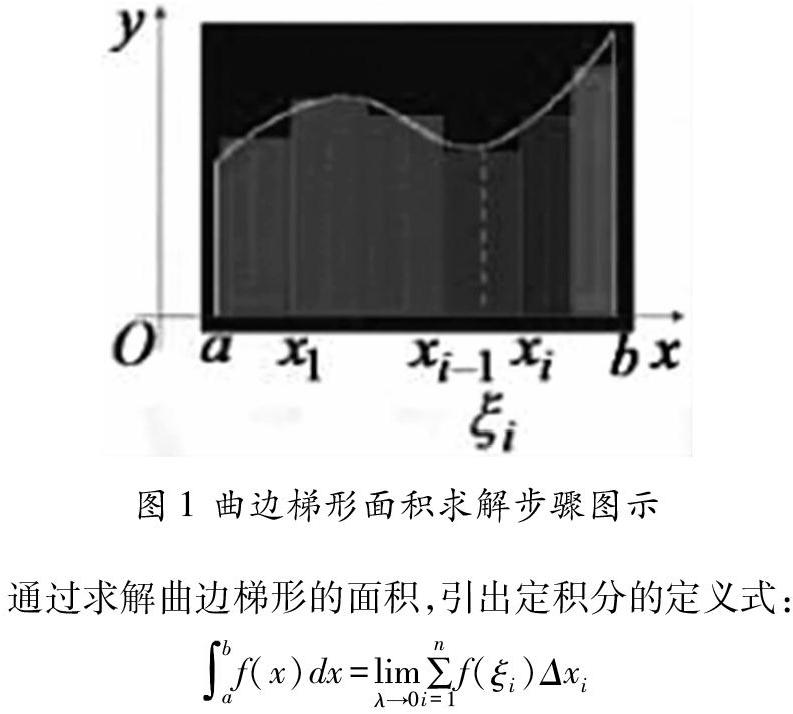
通过观看微课《定积分的概念》，回顾长方形、三角形、梯形、圆形等初等数学中学习的面积求解公式，引出问题：如何求解边界为曲线的不规则平面图形的面积，例如：广西龙里梯田面积、我国国土面积等，该如何求解呢？对上述边界中包含曲线的图形，我们提炼模型特点，引出曲边梯形定义，由曲线y=f（x）及直线x=a，x=b和y=0所围成的平面图形称为曲边梯形。由于曲边梯形的曲边是变化的，所以不能依照之前的各种求面积公式进行计算，于是进一步引出求解曲边梯形面积的步骤：分割、取近似、求和、取极限。

通过求解曲边梯形的面积，引出定积分的定义式：

该定义式中包含了变量在确定区间上无限累加的运算过程。同时，在该过程中体现了以直代曲、量变引起质变、无限与有限相互转化等思想。

第三步：思政元素探讨

曲边梯形面积求解步骤中，每一步都涵盖了思政元素，更是数学这一学科对培养学生核心素养的独特作用的体现。

（1）分割：我们先在区间[a，b]内任意插入n个点，过这些点做X轴的垂涎，这样就可以将曲边梯形分割成很多个小曲边梯形，进而将这个问题转化为先研究小曲边梯形面积的求法。这就像我们在生活或工作中遇到大型任务时，我们可以先将任务进行系统的分解，化为诸多小问题，以便缩小研究范围，进而达到各个击破的效果。

（2）取近似：该步骤的本质是以直代曲的思想，也是化繁为简的体现。其中的转化思想对我们的生活启示很多。在生活或工作中，对遇到的新问题、新任务，可以先转化为已有知识或者成熟的方法来求解，得到一个近似值，虽然不是准确值，但是至少向问题的准确结果更近了一步。在日常生活中，每个人都会遇到一时半会儿过不去的坎儿，比如有时我们会钻牛角尖，不妨试着采取迂回战术，降低一下对准确值的期望，说不定可以达到“以退为进”“柳暗花明又一村”的效果。

（3）求和：将众多的小矩形面积加起来，即积零为整，这是一种迈向准确值的过度，只有通过对比该结果与准确值的差距，才会得出下一步的做法依据，产生新的灵感。所以处理事情，固然需要追求精益求精，但是不一定能够一次性到达完美状态，需要我们脚踏实地得走好每一步，而且每一步必然会发挥其不可替代的作用。这与战国时期思想家、文学家荀子在《劝学》中所主张的“故不积跬步，无以至千里;不积小流，无以成江海”的思想不謀而合。

（4）取极限：通过小曲边梯形个数的无限增加，即无限细化小曲边梯形的宽度，我们就得到了曲边梯形面积的准确值，此步骤可以简记为“抛光磨平”。在此过程中，我们看到了经过无限努力，我们得到了最完美的结果，这也正是量变引起质变的体现，意味着我们面对学习，面对人生，想要达到最好的状态，展现个人最美好的价值，需要踏踏实实做好每一天的努力，人生的成功必然来源于无数个一点一滴的积累。

综上所述，在定积分概念引出前，我们对曲边梯形面积的求法进行了深入研究，在此过程中，总结出求解该类问题的统一步骤，这一步骤正是体现出了定积分定义式的内涵。

第四步：定积分定义式拓展延伸

通过学习曲边梯形面积的求解方法，我们得出了定积分的定义式，下面通过一个富含人生哲理的定积分定义式来检测一下学生对该定义的内涵是否达到了真正理解的地步。

若Value=DeathBirth Studyd（Time），該表达式涵盖了怎样的人生哲理呢？

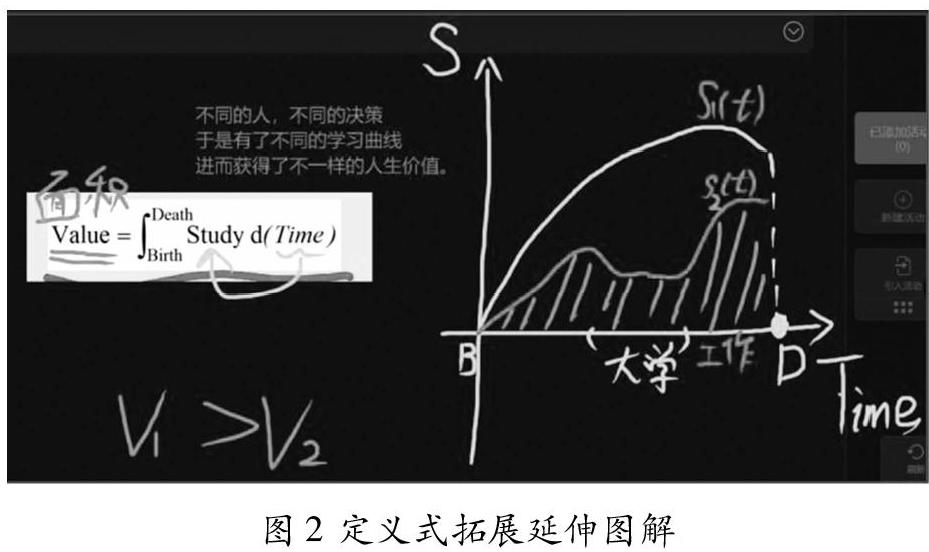
该表达式可以翻译为：人生的价值等于以时间为积分变量的学习函数，从生到死区间上的定积分，参照曲边梯形面积的求解步骤，我们也可以做出一个该定义式的图像：在二维平面中，以时间Time为横轴，以学习量Study为纵轴作出直角坐标系，在区间[Birth，Death]上画出不同的Study曲线（学习量必然非负），那么由x=Birth，x=Death，Study曲线和横坐标轴四条曲线围成图形的面积就是人生的价值。

该定义式蕴含的具体含义是：人生价值的体现，在于从出生到死亡的整个过程中，每时每刻连续不断学习的积累。不同的人，在不同阶段决策不同，对于学习的态度和付出不同，因此Study曲线的走势也各不相同，于是四条曲线围成图形的面积大小就不同，进而呈现出了不同的人生价值。这就意味着我们要不断地学习和积累，才能让自己的人生变得更有价值。正如袁亚湘院士在《开讲啦》节目中所说：“实际上每个人之所以成为我们自己，也是因为我们在不同的阶段做不同的决策，导致我们不同。”万事万物都要遵循最优规律，虽然我们无法控制生与死的命运，但是我们每个人都要珍惜时光，用优化的思想来武装我们的头脑，干什么事情都要尽我们最大的努力做到最好。

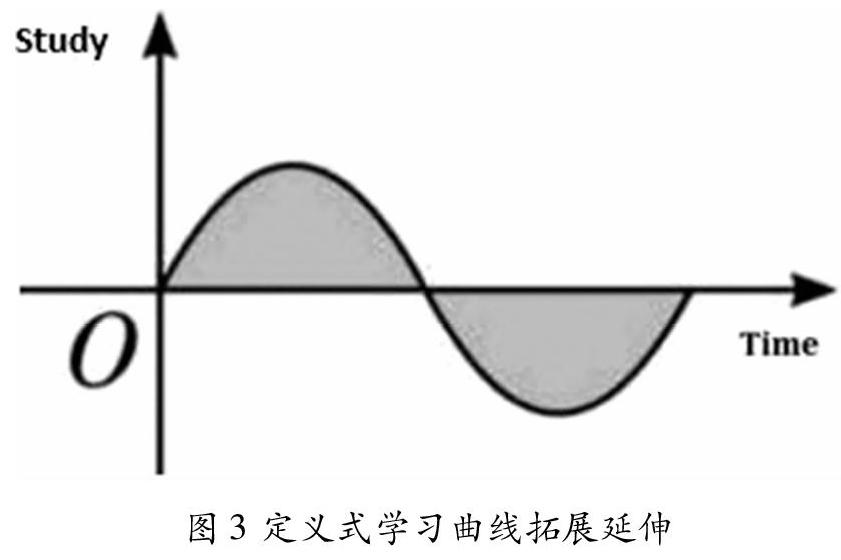
思考与练习：假如学习曲线随着时间的推移有正有负（如图3），那么人生价值又如何解释呢？我们可以将该曲线的含义解释为：随着时间的推移，我们学习的正能量越多，定积分的值越大，人生价值也越大;随着时间的推移，如果我们学习的动力下降，甚至学会了投机取巧，学习一些不好的品质，那么我们得出的定积分的值反而会下降，甚至会有价值归零的危险。综上所述：“学如逆水行舟，不进则退”。

三、课后

在课后，教师在职教云平台布置题库作业，并设置思考题：“简述定积分和不定积分的区别和联系”，不仅提升了学生归纳总结的能力，还能直观检测学生对本次课知识的掌握程度。同时，教师可以提倡学生做出自己的人生学习规划，画出相应的学习曲线（每个人对曲线含义的解释可以不同，这也能够体现出学生思维方式和角度的多样化），从中明白“活到老、学到老”的道理，未来学有所成，为祖国的繁荣昌盛发挥出自己最大的价值。

四、反思与改进

本次课主要是探究定积分的概念，一般情况下学生对数学概念的学习缺乏兴趣，并且概念本身的内容确实抽象难懂，教师通过前期的问题引入等活动，激发学生学习知识并解决问题的欲望。同时，在求解实际问题时，对所应用到的数学方法和思路中融入了思政元素，让学生切切实实感受到数学为自己的生活、未来工作等带来的不可替代的作用，体会数学的实用性和人文价值。最后，在知识拓展学习的过程中，学生从数学知识或者数学方法本身感悟到了其中的人生哲理，对后续的人生规划和奋斗方向产生了深远的影响，达到了教书育人的目的。

另外，在高等数学课程中融入思政元素，要注重与知识和方法的有机结合，倡导“润物细无声”，而不是生搬硬套，或者是单纯独立的一个思政环节。因此，在后续的教学过程中，教师要结合学生专业、学生特点等，积极挖掘数学知识中蕴含的思政要素，整合教学内容的设置，也可以对教科书内容进行适当的拓展，结合时事热点或者难点问题，在寻找解决办法的过程中，呈现数学知识和方法的强大，真正达到“做中学”的目的，最终构建“三全育人”体系，提高育人质量。

五、结语

课程是教育思想、教育目标和教育内容的主要载体，而课堂教学是课程的直接表现形式。课程思政工作只有贯穿于每一次课堂教学，才能充分发挥其立德树人的独特功效。数学课程对学生核心素养的培养需要每一位教师深入挖掘课程内容所蕴含的思想政治教育功能，构建全员全程全方位育人大格局，以核心素养为导向的高职数学课堂教学实践，必将推动高职数学教育教学改革的发展。

参考文献：

[1]罗静.从数学核心素养看高等数学[J].韶关学院学报，2017（5）：83-85.

[2]曲元海，于海菊，等.高等数学核心素养探析[J].通化师范学院学报，2019（5）：72-75.

[3]胡楠.定积分的发展史和应用[J].科技尚品，2017，3：250-256.

[4]教育部.高等学校课程思政建设指导纲要.2020-5-28.

[5]黄新宇，王修建，岳芹.课程思政元素融入高等数学的教学研究——以数列极限为例[J].浙江万里学院学报，2020，7：101-105.

作者简介：雷艳玲（1985— ），女，汉族，河北石家庄人，硕士，讲师，研究方向：决策科学。