例谈求解圆的方程常用方法

杜红全

(甘肃省康县教育局教研室 746500)

圆是简单的二次曲线，是高中数学的一个基本内容，也是高考常考的内容，会求圆的方程才是硬道理.下面举例说明求圆的方程的常用方法，供参考.

一、直接法

直接法就是根据圆的定义，利用已知条件，确定圆心坐标和半径，直接求出圆的标准方程.

例1求满足下列条件的圆的方程：

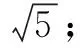
(2)经过点P(5,2)，圆心是点C(4,-1).

分析根据题设条件，可利用圆的方程的定义来解决.

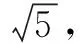
点评确定圆的标准方程只需要圆心的坐标和圆的半径即可，因此圆心和半径是圆的两要素.

二、几何性质法

几何性质法就是通过研究圆的性质、直线和圆、圆和圆的位置关系，求出圆心坐标与半径，从而得到圆的标准方程. 常用的几何性质有：圆心与切点的连线垂直于切线；圆心到切线的距离等于圆的半径；圆的弦的垂直平分线过圆心；两条弦的垂直平分线的交点为圆心等.

例2 求过点A(1,-1)和B(-1,1)，且圆心在直线x+y-2=0上的圆的方程.

分析利用圆的几何性质求出圆的圆心和半径后，再写出方程.

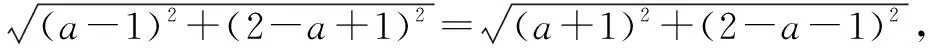
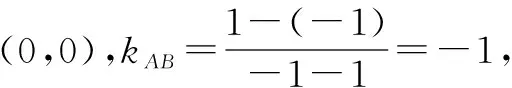
点评一般地，在解决有关圆的问题时，有时利用圆的几何性质作转化较为简单，充分体现了解析几何问题的代数方法和几何方法的有机结合的特点.本题还可以用待定系数法求解.

三、待定系数法

圆的方程中，有三个独立系数，因此必须具备三个独立条件才能确定一个圆，确定系数的方法就是待定系数法.待定系数法就是先设出圆的方程，然后根据条件求出方程中的参数.

1. 设圆的标准方程

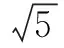
分析可设出圆的标准方程，再把A,B两点的坐标代入，用待定系数法求解.

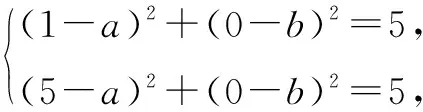
点评如果由已知条件容易求得圆心坐标、半径或需要利用圆心的坐标或半径列方程问题，一般采用圆的标准方程，再用待定系数法求出a,b,r.本题还可以用几何性质法求解.

2.设圆的一般方程

例4 已知△ABC的三个顶点为A(1,4),B(-2,3),C(4,-5),求△ABC的外接圆方程.

分析已知三个顶点都在圆上，可采用圆的一般方程，利用待定系数法求出圆的方程.

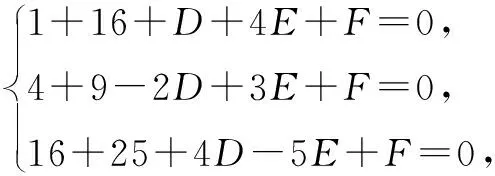
点评如果已知条件与圆心和半径都无直接关系，通常采用圆的一般方程，再用待定系数法求出常数D,E,F；本题还可以用几何性质法求解.

四、利用圆的直径式方程

已知一个圆的一条直径的端点是A(x1,y1)，B(x1,y1)，则圆的方程可表示为(x-x1)(x-x2)+(y-y1)(y-y2)=0，此方程称为圆的直径式方程.

例5 求过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点，且面积最小的圆的方程.

分析设直线和圆的交点为A，B，面积最小的圆是以AB为直径的圆.故可以利用圆的直径式方程求解.

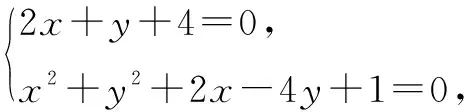
点评求解本题的关键是知道面积最小的圆是以直线和圆的交点为直径的圆，此题虽然还可以利用圆的性质求出圆心的坐标和半径求解，但是用圆的直径式方程求解比较简便.当然本题还可以用过直线与圆交点的圆系方程求解.

五、利用圆系方程

具有某种共同性质的圆的集合叫做圆系，含有参数的圆的方程称为圆系方程.常用的圆系方程类型有以下几种：

(1)同心圆系①以(a,b)为圆心的同心的圆系方程为(x-a)2+(y-b)2=λ2(λ为参数，λ>0)；②与圆x2+y2+Dx+Ey+F=0同心的圆系方程为x2+y2+Dx+Ey+λ=0(λ为参数)；同心圆系图形特点是位置相同，大小不同.

(2)半径相等的圆系方程为(x-m)2+(y-n)2=r2(m、n为参数)，图形特点是大小一样，位置不同.

(3)过直线与圆交点的圆系方程.设直线l:Ax+By+C=0与圆C:x2+y2+Dx+Ey+F=0相交，则方程x2+y2+Dx+Ey+F+λ(Ax+By+C)=0(λ为参数)表示过直线l与圆C的两个交点的圆系方程.

(4)过两圆C1:x2+y2+D1x+E1y+F1=0和C2:x2+y2+D2x+E2y+F2=0交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ为参数，λ≠-1，且不含圆C2)，特别提示：①由于该圆系方程不包括圆C2，因此直接应用该圆系方程必须检验C2是否满足题意，谨防漏解；②当参数λ=-1时，该方程为过两圆交点的一条直线方程：(D1-D2)x+(E1-E2)y+(F1-F2)=0.

例6 有一圆与直线l:4x-3y+6=0相切于点A(3,6)，且圆经过点B(5,2)，求此圆的方程.

分析将点A(3,6)视为“点圆”:(x-3)2+(y-6)2=0，然后利用过直线与圆交点的圆系方程求解.

解根据题意可设所求圆的方程为(x-3)2+(y-6)2+λ(4x-3y+6)=0，把点B(5,2)的坐标代入方程，解得λ=-1.所以所求圆的方程为x2+y2-10x-9y+39=0.

点评所谓“点圆”就是半径为0的圆，所以一个孤立的点C(a,b)的图形可以看成“点圆”，即点C(a,b)的圆的方程可表示为(x-a)2+(y-b)2=0，在求与已知直线或已知圆相切于某一已知点的圆的问题时，把切点视为“点圆”是一个重要方法技巧.本题还可用几何性质法和待定系数法求解.

例7 求以圆C1:x2+y2-12x-2y-13=0和圆C2:x2+y2+12x+16y-25=0的公共弦为直径的圆的方程.

分析可先求公共弦所在直线的方程，再利用过两圆交点的圆系方程求解.

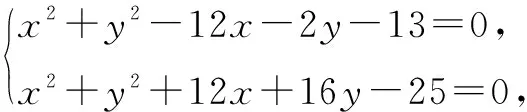
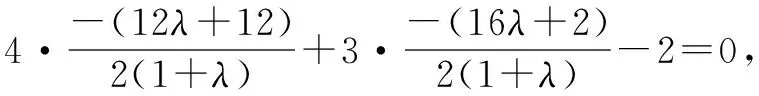
点评一般地，求过两个圆交点的圆的方程利用圆系方程求解比较简捷，应学会使用此法.本题还可先求出公共弦的端点坐标，再得所求圆的方程.